On the one hand it is a pity I have to remove the previous post from the top position. Never ever I would have thought that the Voyager probes would be a big help in my quest of proving that electrons are not magnetic dipoles. Electrons are magnetic monopoles, if your local physics professor thinks otherwise why not ask you local physics professor for the experimental evidence there is for the electron magnetism dipole stuff?
On the other hand this post is about Gaussian intergers for the 3D complex and circular numbers and it is with a bit of pride that I can say we have a bunch of beautiful results because the last theorem of Fermat does not hold in these spaces.
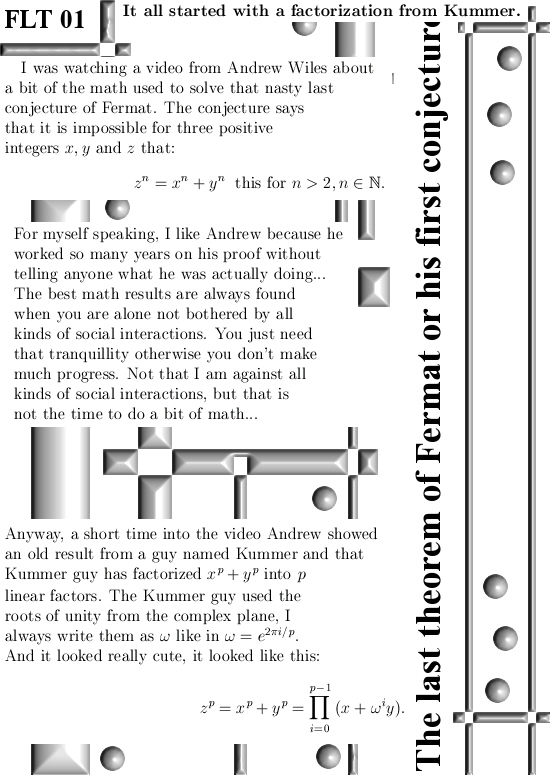
The last theorem of Fermat is a kind of negative result, it says that it is impossible for three integers x, y and z that x^n + y^n = z^n, this for integer values of n greater than 2 of course. (For n = 2 I think most readers know it is possible because those are the Pythagoras triples.)
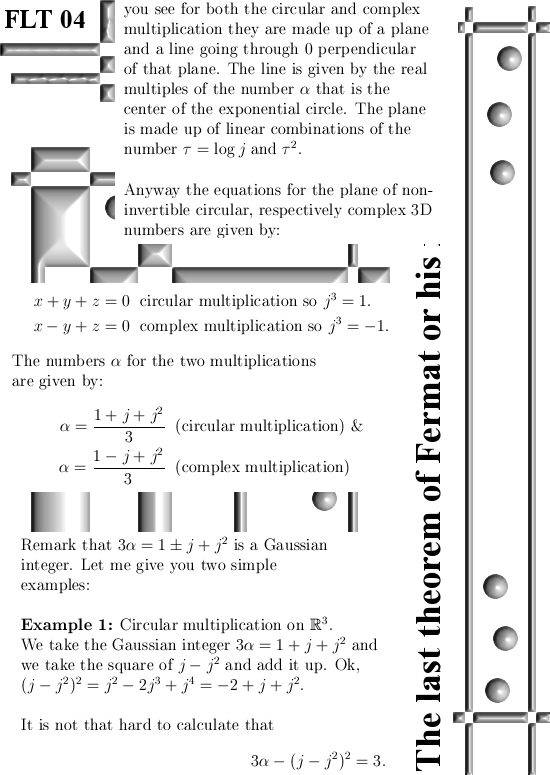
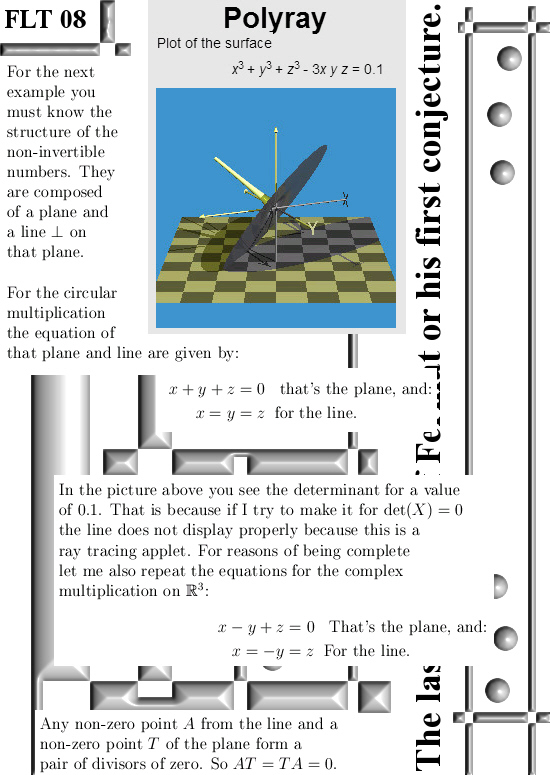
Anyway I succeeded into writing the number 3 as the sum of two Gaussian 3D integers that are also divisors of zero. So this pair of integers, in this post I name them A and T because they are related to the famous 3D numbers alpha and tau, are divisors of zero so as such AT = 0. As such as a denial of the Fermat theorem, an important result as posted here is that A^n + T^n = 3^n. So on the 3D complex & circular numbers this result is possible while if you use only the 2D complex plane and the real line this is not possible…
But there are plenty of spaces where the Fermat conjecture or the last theorem does not hold. A very easy to understand space is the ring of integers modulo 15. In this ring there are numbers that do not have a multiplicative inverse, say 3 and 5. And if inside this ring you multiply 3 and 5 you get 15 and 15 = 0 in this ring… Hence inside this ring we have that 8^n = 3^n + 5^n (mod 15) also contradicting the Fermat stuff.
I did some internet searches like ‘Fermat last theorem and divisors of zero’ but weirdly enough nothing popped up. That was weird because I view the depth of the math results related to this divisor of zero as the depth of a bird bath. It is not a deep result or so, just a few centimeters deep. But sometimes just a few centimeters can bring a human mind into another world. For example a long time ago when I still was as green as grass back in the year 1986 I came across the next excercise: Calulate the rest of 103 raised to 103 and divided by 13. I was puzzled, after all 103^103 is a giant number so how can you find the rest after dividing it by 13? But if you give that cute problem a second thought, after all that is also bird bath deep because you can solve it with your human brain…
This post is 11 pictures long, all of the standard size of 550×775 pixels. Because I could not find anything useful about the last Fermat theorem combined with divisors of zero I included a small addendum so all in all this post is 12 pictures long.








After so much Gaussian integer stuff, there is only one addendum about the integers modulo 30. In that ring you can also find some contradictions to the standard way of presenting the last theorem of Fermat.

Ok, if you are still fresh after all that modulo 30 stuff, for reasons of trying to paint an overall picture let me show you a relatively good video on the Kummer stuff. Interesting in this video is that Kummer used the words `Ideal numbers´ and at present stuff like that is known as an ideal. For myself speaking I never use the word ´ideal´ for me these are ´multiplicative attractors´ because if a number of such an ideal multiplies a number outside that ideal, the result is always inside that ideal. Here is a relatively good video:
And now you are at the end of this post. Till updates.

