I finished the proof that was originally meant to be an appendix to the previous post. And I have two more or less small things I want to share with you so lets get started with the first thing:
Thing 1: Tibees comes up with a very cute program of graphing 3D surfaces. It’s name is surfer, the software is very simple to use and it has the giant benefit of making graphs from implicit equations like
f(x, y, z) = 0. For example if you want the unit sphere in 3D space you must do x^2 + y^2 + z^2 – 1 = 0. Now for this website I always used an internet applet that uses ray tracing and by doing so over the years such graphs always look the same. But this surfer program has cute output too and it has the benefit you don’t need to be online. Here is how such a graph looks, it is the determinant in the space of 3D complex numbers, to be precise it shows the numbers with a determinant of 1:

By the way, the surface of this graph is a multiplicative group on it’s own in 3D space. I never do much group stuff but if you want it, here you have it. And for no reason at all I used GIMP to make one of those cubes from the above graph. It serves no reason beside looking cute:
The Tibees female had a video out last week where she discusses a lot of such surfaces in three dimensional space using that surfer software. And she is a pleasant thing to look at, it is not you are looking at all those extravert males drowning in self-importance only lamentating shallow thoughts. The problem posed in the video is an iteresting one, I don’t have a clue how to solve it. Title of the video: The Shape No One Thought was Possible. It is a funny title because if you start thinking about all the things that math professors thought were not possible you can wonder if there is enough paper in the entire universe to write that all out..
Link to the Surfer program in case you want to download & install it:
https://www.imaginary.org/program/surfer.
Thing 2: The last weeks it is more and more dawning on me that all those centuries those idiots (the math professors) did not find counter examples to the last theorem of Fermat. Nor was there any improvement on the little theorem of Fermat. Only Euler did some stuff on the little theorem with his totient function, but for the rest it is not much…
Well since Jan of this year I found many counter example to the last theorem of Fermat and in my view I made a serious improvement on the little theorem of Fermat.
So is the improvement serious or not?
Here is a picture that shows the change:

On a wiki with a lot of proofs for the little theorem of Fermat they start with a so called ‘simplification’. The simplification says that you must pick the number a between 0 and p. So if you have an odd prime, say a = 113, does the little theorem only make sense for exponents above 113?
And can’t we say anything about let’s say the square 113^2?
With the new version of the little theorem we don’t have such problems any longer. Here is a screen shot from the start of that wiki, the upper part shows you the improvement:

If you follow that link you can also scroll down to the bottom of the wiki where you can find the notes they used. It is an impressive list of names like Dirichlet, André Weil, Hardy & Wright and so on and so on. All I want to remark is that non of them found counter examples to the last theorem nor did they improve on the little theorem of Fermat. Now I don’t want to be negative on Dirichlet because without his kernel I could never have crafted my modified Dirichlet kernel that is more or less the biggest math result I ever found. But the rest of these people it is just another batch of overpaid non performers. It’s just an opinion so you don’t have to agree with it, but why do so many people get boatloads of money while they contribute not that much?
End of thing 2.
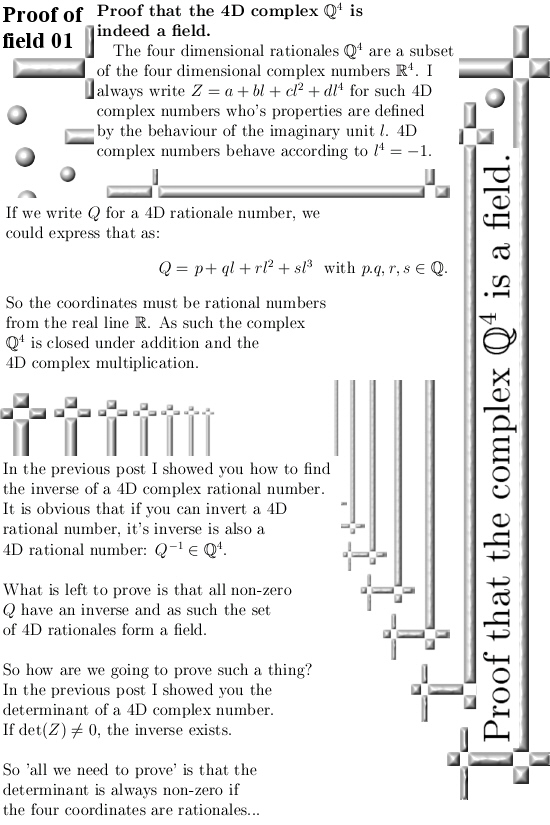
Now we are finally ready to post the main dish in this post: the proof that the subset of four dimensional rational numbers form a field. Math professors always think it is ‘very important’ if something is a field while in my life I was never impressed that much by it. And now I am thinking about it a few weeks more, the less impressed I get by this new field of four dimensional complex numbers.
Inside the theory of higher dimensional complex numbers the concept of ‘imitators of i‘ is important: these are higher dimensional numbers that if you square them they have at least some of the properties of the number i from the complex plane. They rotate everything by 90 degrees or even better they actually square to minus one.
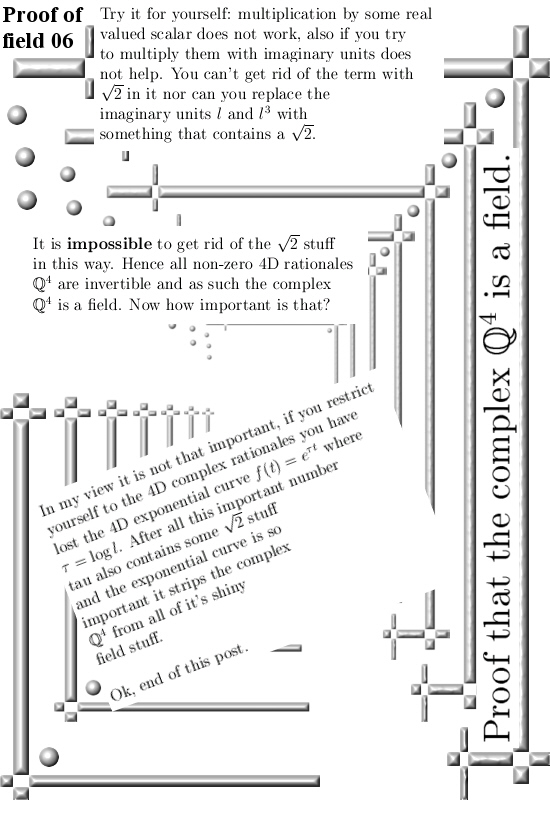
Well one of the imitators of i in the space of 4D complex number is dependent of the square root of 2. As such it is not a 4D rational complex number. That detail alone severely downsizes my enthousiasm.
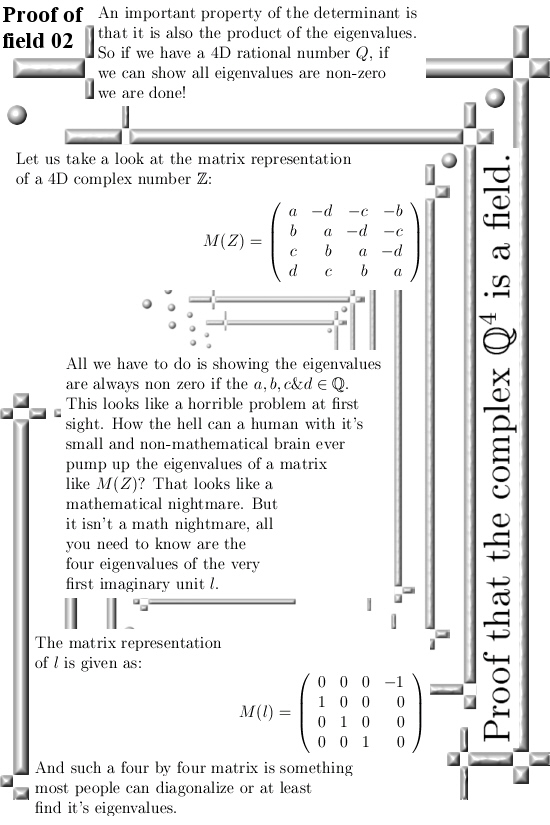
But anyway, the next pictures are also a repeat of old important knowledge like the eigenvalue functions. Instead of always trying to get the eigenvalues from some 4×4 matrix, with the eigenvalue functions with two fingers in your nose you can pump out the eigenvalues you need fast. This post is six pictures long each size 550×825 pixels.
Here we go:



Yes that is the end of this post that like always grew longer than expected. If you haven’t fallen asleep by now, thanks for your attention and don’t forget to hunt the math professors until they are all dead! Well may be that is not a good idea, but never forget they are too stupid to improve on the little Fermat theorem and of course we will hear nothing from that line of the profession…