Already a few years back I wanted to write a post on the so called de Padé apprximations because they are so good at taking the logarithm of a matrix. For me the access to an internet application that calculated those logs from matrix representations was a very helpful thing to speed things up. It would have taken me much much longer to find the first exponential circle on the 3D complex numbers if I could not use such applets.
But in the year 2018 pure evil struck the internet: the last applets or websites having them disappeared to never come back. Ok by that time I had perfected my method of simply using matrix diagonalization for finding such logs of matrices. You can still find it easily if you do an internet search on ‘Calculation of the 7D number tau‘.
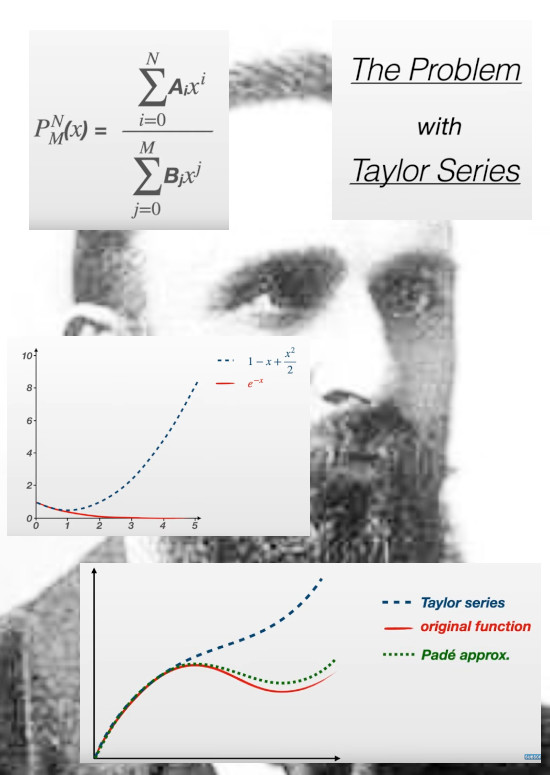
Yet in the beginning I only had such applets as found on the internet and I soon found out that using the so called de Padé approximation always gave much better results compared to say a Taylor approximation.
It is not very hard to understand how to perform such a de Padé approximation. Much harder to understand is how de Padé found them, after all it looks like a strike of genius if this works. The genius part is of course found in the stuff you can simply neglect in such approximations, at first it baffles the mind and later you just accept it that you are more stupid as de Padé was…;)
Anyway this week I stumbled upon a cute video and as such I decided to write a small post upon this de Padé stuff. (On the shelf are still a possible new way of making an antenna based on the 3D exponential circles and some updates on magnetism.)
So let us first take a look at the video, here we go:

As you see the basic idea is pretty simple: you use those two polynomials to ‘approximate’ that Taylor series and as a bonus you have a much better approximation of the original function. All in all this is amazing and it makes you wonder if there are methods out there that are even better compared to this de Padé approximation.

Now you can choose beforehand what degree polynomial you use in the nominator and denominator. There are plenty of situations where this brings a big benefit like in the video they point out the divergence problems of say the sine function that is bounded between +1 and -1 on the real axis. The Taylor approximations always go completely beserk outside some interval where they fit quite well. With the appropiate choice of the degrees of the polynomials in the de Padé approximation you can avoid this kind of stuff.
In my view the maker of the video should also have pointed out that a de Padé approximation can have it’s own troubles when you divide by zero. And when the original function never has such a pole at that point, the de Padé approximation also goes very bad. These de Padé approximations
are indeed much better compared to the average Taylor approximation but they are not from heaven. You still have to use your own brain and may be that is a good thing.

In this post I did not cover the matrices and why a de Padé approximation of the logarithm of a matrix is good or bad. If you want to find exponential circles and curves for yourself, use those applets mostly on imaginary units who’s matrix representation has a determinant of +1. In case you want to find your very first exponential circle, solve the next problem:

Ok, it is late at night so let me hit that button ‘publish website’ and see you around.