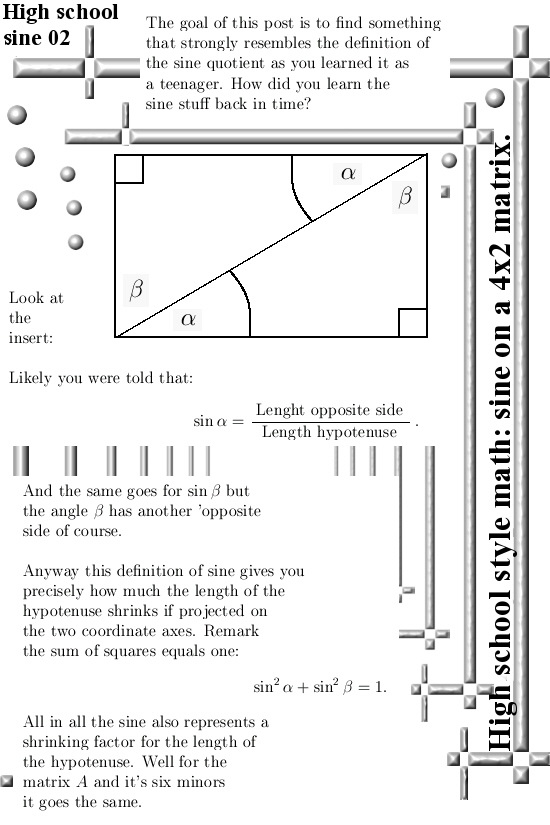
A long long time ago you likely learned how to calculate the sine in a rectanglular triangle. And that was something like the length of the opposite side devided by the length of the hypotenuse. But now we have those simple expressions for the volume of a non-square matrix, we can craft ‘sine like’ quotients for the minors of a matix against it’s parent matrix.
I took a simple 4×2 matrix so 4 rows and 2 columns, wrote out all six 2×2 minors and defined this sine like quotient for them. As far as I know this is one hundred percent useless knowledge, but it was fun to write anyway.
Likely also a long time ago you learned that if you square the sine and cosine of some angle, these squares add up to one. In this post I formulated it a little bit different because I want to make just one sine like quotient and not six ones that are hard to tell them apart. Anyway, you can view these sine like quotients as the shrinking factor if you project the parent matrix onto such a particular minor. With a projection of course you leave two rows out in you 4×2 parent matrix, or you make these rows zero. It is just what you want.
The parent 4×2 matrix A we use is just a two dimensional parallelogram that hangs in 4D space, so it’s “volume” is just an area. I skipped the fact that this area is the square root of 500. I also skipped calculating the six determinants of the minors, square them and add them up so we must get 500. But if you are new to this kind of matrix version of the good ol theorem of Pythagoras, you definitely must do that in order to gain some insight and a bit of confidence into how it all works and hangs together.

But this post is not about that, it only revolves around making these sine like quotients. And if you have these six quotients, if you square them and add them all up, the result is one.
Just like sin^2 + cos^2 = 1 on the real line.

Please notice that the way I define sine like quotients in this post has nothing to do with taking the sine of a square matrix. That is a very different subject and is not a “high school definition” of the sine quotient.
This post is just three pictures long, here we go:

So after all these years with only a bunch of variables in most matrices I show you, finally a matrix with just integer numbers in it… Now you have a bit of proof I can be as stupid as the average math professor…;)

But serious: The tiny fact all these squares of the six sines add up to one is some kind of idea that is perfectly equivalent to the Pythagoras expression as some sum of squares.
Thanks for your attention.