This very short post was written because of a video from the video channel Kathy loves physics. It is one of those “Quaternions are fantastic” video’s. And Kathy just like a lot of other physics people think indeed that quaternions are fantastic. But you cannot differentiate or integrate on the quaternions so I guess this stronly limits it’s use in physics.
But quaternions are very handy in describing rotations in 3D space, I never studied the details but it was said that on the space shuttle it was used for nagvigation. And because of these rotation properties at present day they are used in the games industry.

Anyway in the video Kathy explains that Hamilton did try for a long time to find the three dimensional complex numbers. And he never succeeded in that. Of course I know this for decades right now but in the past I never looked into a tiny bit more detail in what Hamilton was actually doing.
And he was looking at complex numbers of the form X = x + yi + zj where the imaginary components both equal to minus one: i^2 = j^2 = -1.

If you check the easy calculations in this post for yourself, it is amazing how much it already looks like the stuff as found on the quaternions. As such it is all of a sudden much less a surprise that Hamilton found the quaternions. As a matter of fact it was only waiting until he would stumble across them. But at the time the concept of a four dimensional space was something that made you look like a crazy lunatic, there were even vector wars and lots of crazy emotional stuff.

At present day it is accepted that 3D complex numbers do not exist, in my experience the professional math community is still emotionally laden but now into the direction of total neglect. Stupid shallow thought like “If Hamilton could not find them, they likely don’t exist”.

Back in the 19-th century they were always looking for an extenstion of the complex plane to three dimensional space. Of course they failed in that attempt because it is a fact of math life that you cannot solve the equation X^2 = -1 on the space of 3D complex (and also circular) numbers.

The content of this post is just two pictures, after that two more pictures as I used them on the other website and after that you can finally dive into the Video from Kathy. If you are interested in physics and also the history of physics, Kathy her channel is a thing you should take a look at if you’ve never seen it. Here we go:

YES, that is what he should have done. Hamilton tried for about one decade to find the numbers that form the title of this very website, so may be he tried this kind of approach. I don’t know, but the 3D complex numbers are not some extension of the complex plane because 2 is not a divisor of 3. You know that prime number stuff is going on here.
But the math professors are not interested in that kind of stuff.

Here is how I used it on the other website:

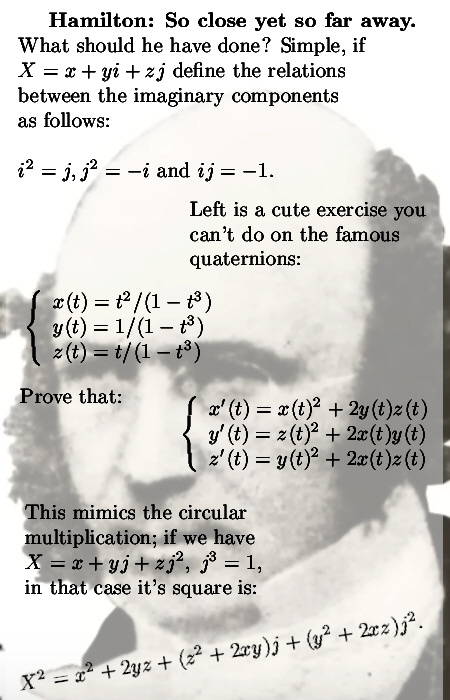
As you see in the above picture I was already working on the previous post because if you differentiate the three functions that mimics the 3D circular multiplication. You can also mimic the multiplication on the complex plane, that is in the next picture:

At last you can view the famous video of Kathy! It’s only 30 minutes or so but if you see too many so called TIKTOK videos that is infinitely long: Wow 30 minutes long looking at just one video?

End of this post, likely the next post is about 4D complex numbers.