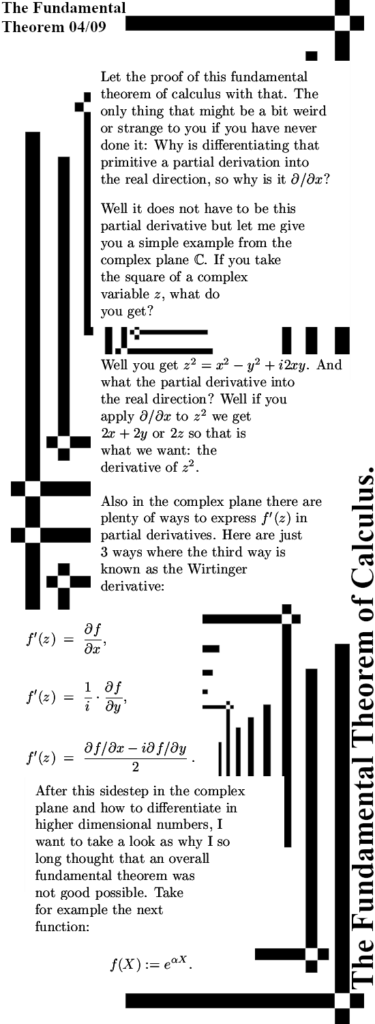
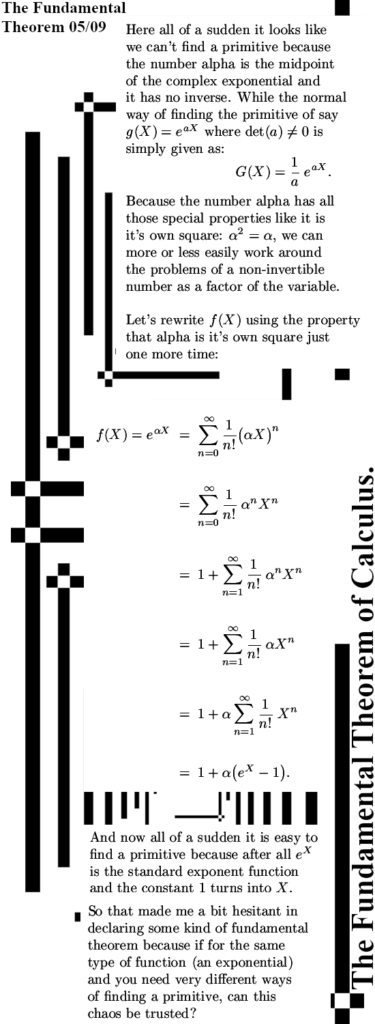
It is already some time ago that I posted the last part of the new ‘General Theory’ series. That was on Oct 28 in 2023 and the last part was about the Cauchy-Riemann equations for n-dimensional real space aka the n-dimensional complex and circular numbers. Since the CR equations govern anything related to differentiation, how to calculate partial differentials and how they relate to each other and most of all: how to find the derivative of a function, you will need that to understand this post. This post is the fundamental theorem of calculus and that is of course integration along a contour of as I often name it a bit wrong ‘line integration’.
Basically the result is the same in all spaces: Under certain mild conditions you can integrate along a contour some function that we name f. And if you do that the result is the difference of some primitive lets name it F in the end points of that curve of integration.
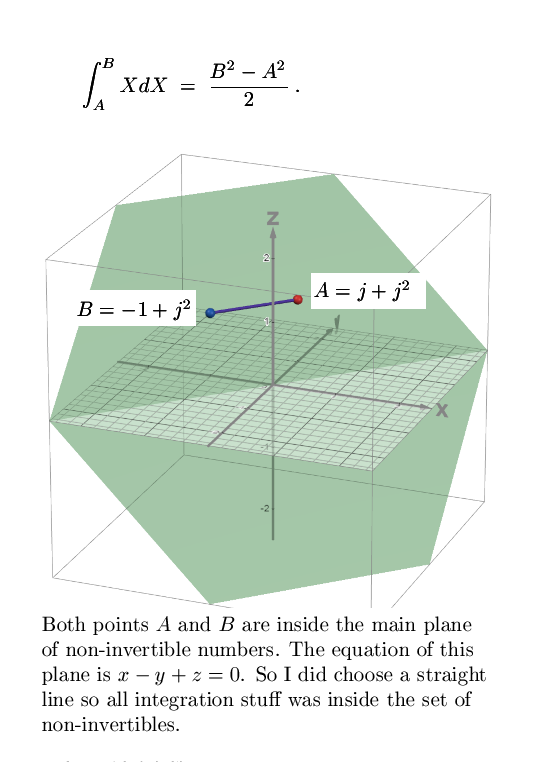
Now in the last post on integration where we looked at the fundamental theorem of calculus for the 3D complex numbers I pointed at the fact it is now the year 2025 and why did it take so long? Well all those years I assumed that getting a primitive F of some function f was not always assured especially when you were integrating in the sub spaces of non invertible numbers that higher dimensional numbers have. And yes there are a boatload of troubles there, sometimes it is very hard to find a primitive and it is not always clear if you will actually find it.
So in this post I turned the troubles upside down and I simply start with a primitive and it is proven that the integral of the derivative of this primitive is the primitive. To put it simple:
1) I have some primitive F or F(X),
2) I differentiate it to get some f or f(X) and
3) I integrate along a curve from A to B and guess what?
4) I get F(B) – F(A).
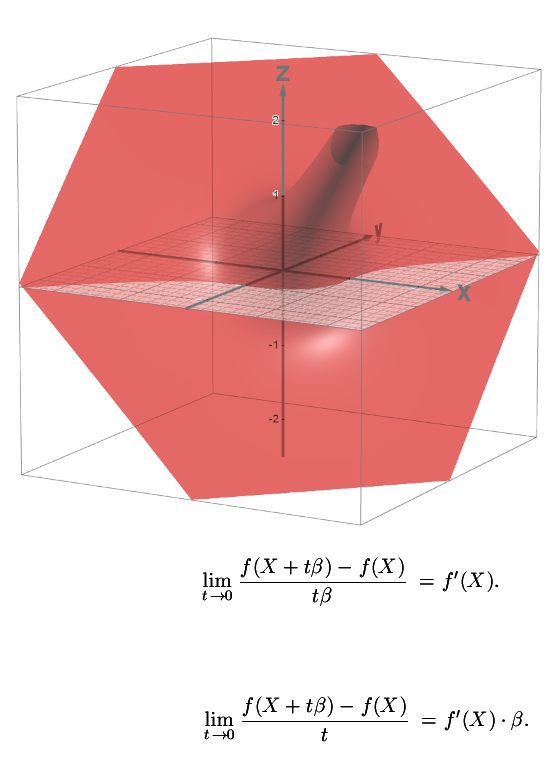
But by doing that, how to find the derivative inside the sub space of non-invertible numbers? After all you can’t devide by then so how to even make sense of the most basic limit for calculating the derivative? From the ‘math technical’ side of things, this was easy to solve with just a tiny modification this division by a non-invertible number can be avoided. With that this approach of starting with a primitive looks like a clean approach without much unsolved problems of understanding.
Weirdly enough it was a easy ‘do-able’ so by just differentiating the set of all primitive functions I could avoid proving the existence of primitives when you take the integral of some function f.
The post is six images long and have size 550×1500 pixels, there are an additional two images in the appendix where I work out the primitive of ZdZ in the space of 4D complex numbers.







So lets recap what we have done in this post: In case it is correct that this universe is 13.8 billion years old, in that case the math professors have found only three versions of the fundamental theorem of calculus. They have two slightly different versions for the real line and one for the complex plane. So basically they only have two Fundamental Theorems of Calculus.
In this post we looked at the n-dimensional real spaces equipped with either the complex or the circular multiplication. So for every fixed dimension n there are two fundamental theorems related to those two multiplications. As such in this post we found an infinite number of fundamental theorems so although I don’t like it to write general theory, all in all this was not a bad day at the office.
Because I never made a so called ‘category’ of general theory on this website you must use the search function or use the next internal links:
Proof that Z^2 = -1 cannot be solved on real spaces with an odd dimension. (General theory part 1.)
General theory Part 2: On a matrix named big E.
General Theory Part 3: Cauchy-Riemann equations.
So for the time being included this post General Theory Part 4 on integration, for the time being, this is all general theory that there is. It contains the ancient quest for a number who’s square equals minus one. The matrix big E is handy if you want to study all kinds of multiplications while part 3 and 4 cover differentiation and integration.