In the last seven years it has taken me a long time to arrive at the conclusion that electron spin is a permanent property of electrons. The only place in this universe where electrons get their spin flipped is in the head of physics professors.
For new readers: The last years I work from the hypothesis that electrons are magnetic monoples but every now and then I still try to kill that idea. But I always fail, in the end the electrons having a monopole magnetic charge always wins it from models like the ‘tiny magnet’ model for electrons. Why took it so long for me to finally accept this ‘permanent’ status of electron spin or as I say it: electron magnetic charge?
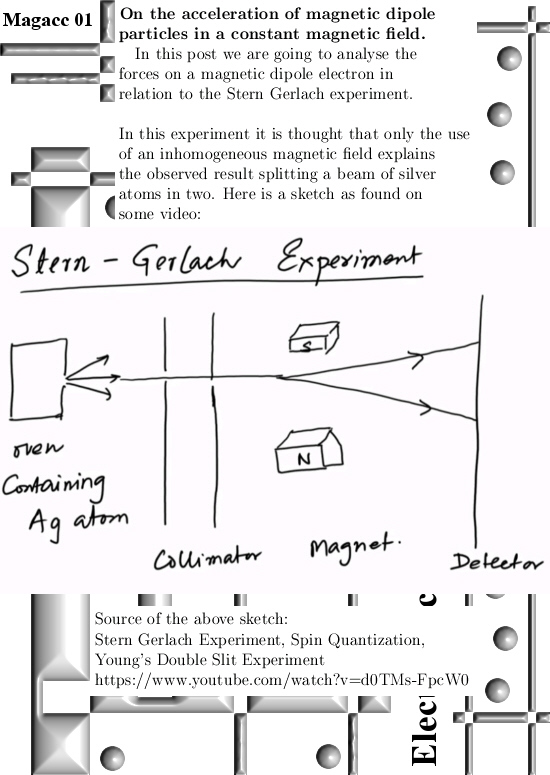
Well there are a lot of video’s out there where people from physics explain how they flip electron spin while building quantum computers. At the end I post a long video from a guy named Lieven Vandersypen who works at the Technical University in Delft. Now I do not hate these people but when I say for seven years on a row ‘Where is you experimental proof that electrons are indeed tiny magnets?’.
If seven years on a row just nothing happens over there we can safely conclude that Mr. Vanderlieven is just another UI. And an UI is a person that is an Ultimate Idiot or if you want an Ultra Ignorant.

In the theory of quantum mechanics before a measurment is done, it is assumed that a quantum particle is in a superposition of all possible states the quantum particle can be in.

Physics professors think that all electrons are the same and as such it has to be that before the measurement of the electron spin it is always in a superposition of spin up and spin down.

Remark this is very different from what I think: If the monopole magnetic charge is permanent, repeated measurments should always give the same magnetic charge. Just like measuring the electric charge of an electron always returns that is has one unit of negative electric charge…

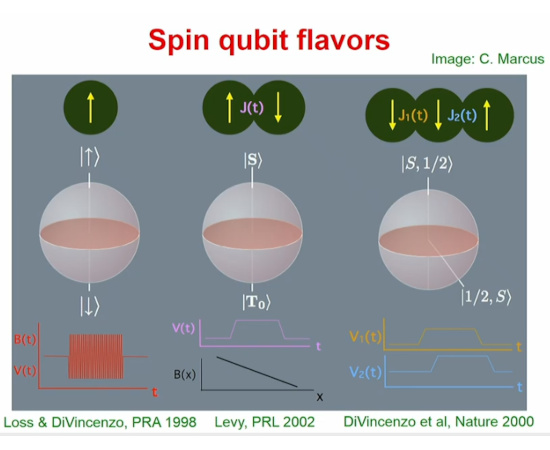
In the present hype of building quantum computers, almost 100% of the physics people think that it is possible that the electron is in some super position of spin up and spin down. I think this is not possible because we are having two different kind of electrons in this universe. If true you can wonder how far astray physics has driven from reality; in the next screen shot you see Mr. Vandersypen wonder what kind of qubit is the best for quantum computing. He says that they have been wondering for years what basic configuation of electron spins as qubits is the best.
They think that every electron can be in a super position of spin up and spin down. On top of that if you have an electron pair they think it is in a super position of spin up-down with spin down-up, that is that Bell stuff.

If my view on electron spin is correct, all these approaches in quantum computing will never work. Here is how these fantasies look:

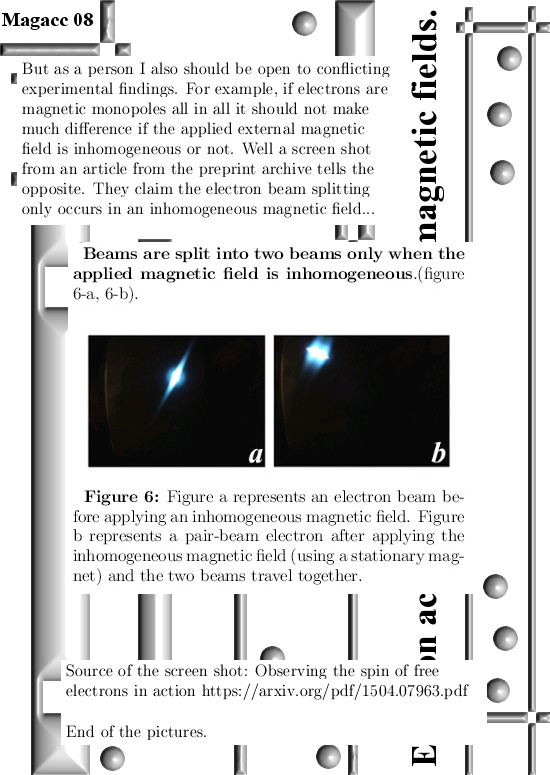
Now have you ever heard of an electron triple like in the right of the above picture? Why are there only electron pairs or unpaired electrons found in nature? That is because electrons are magnetic monopoles and that is why the electron pair is magnetically neutral while the unpaired electron is not magnetically neutral.

Compare that to the electric charge of the hydrogen atom. All in all it is neutral because the electric charges cancel each other out. So you can’t accelerate atomic hydrogen with electric fields until the electric field gets so strong it rips apart the hydrogen atoms. So why are electrons accelerated by magnetic fields and electron pairs not? After all if the electrons are ‘tiny magnets’ are they not supposed to be neutral when it comes of magnetic fields?

The title of this post says I have to give you some reasons as why electron spin or magnetic charge is permanent. So lets try a bit:

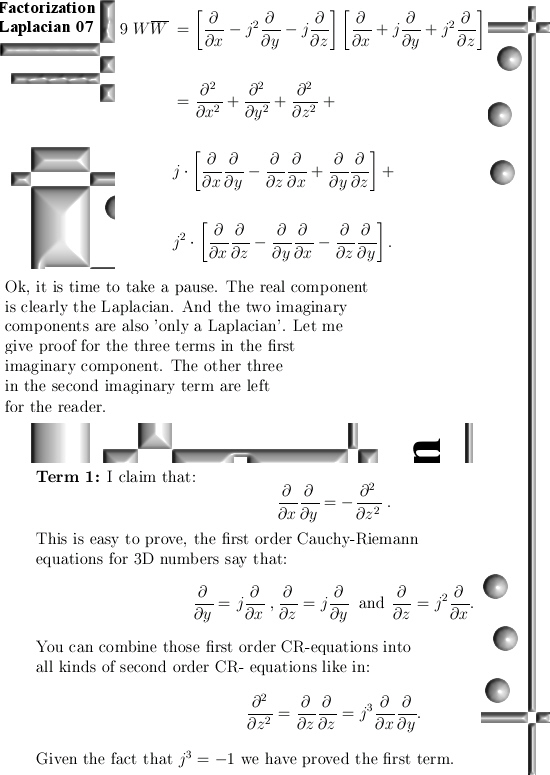
Reason 1) The official version of electron spin is that if you measure it in one direction, say the direction of an x-axis in a 3D coordinate system, that gives a reset for measuring electron spin in perpendicular directions say the y and z-axis. But any interaction with a magnetic field is a measurement in some direction.
So these weirdo’s try to tell us that electron spin flips all the time because after all there are a lot of magnetic fields around us all the time.
In the previous post I showed you the weird result that oxygen has a so called non-binding pair of electrons. That’s why it is magnetic. But molecular oxygen O2 is stable, if you apply magnetic fields to it no spin reset is observed. The non-binding pair does not change and all other electron pairs also don’t do weird stuff and the oxygen molecule stays stable under application of all kinds of magnetic fields.

Reason 2) The (hyper, see correction and addendum at the end) fine spectral structure of atomic hydrogen. There are very small differences in energy levels of the electrons in atomic hydrogen. The official version is that the electron spin and nuclear spins are aligned or anti-aligned. Of course it is never explained how an electrons supposedly going around the nucleus with high speed maintains it’s alignment…
In my view where electron and proton spin are just magnetic charges, it is all blazingly simple: there must be four variants of atomic hydrogen when it comes to spin. Proton spin up or down combined with an electron with spin up or down. When both proton and electron have the same spin, the electron will be in that slightly higher energy level.
And if the spins in atomic hydrogen are opposite, the electron has a bit lower energy because after all magnetic opposite monopoles attract.

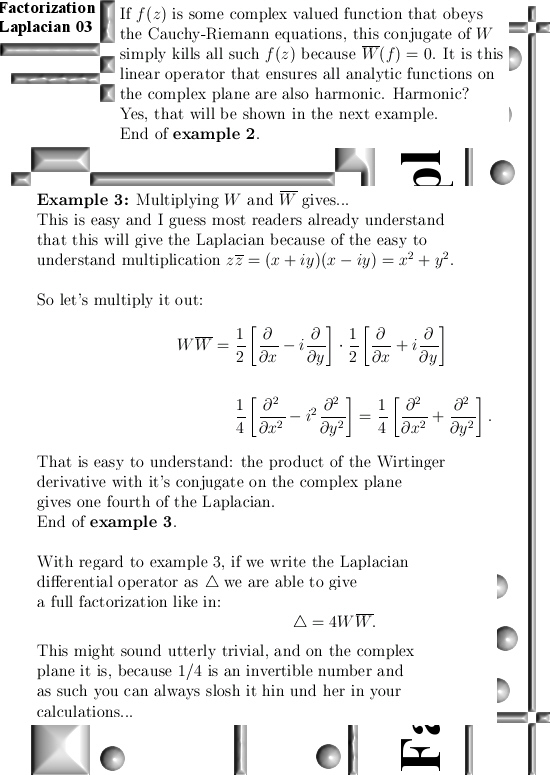
Reason 3) A very interesting observation of the ESO (European Southern Observatory), it is about sun spots and different sun spots give different circular photons in the light coming from those sun spots. I have to collect more evidence that circular photons with opposite circular polarization are produced by electrons with opposite spins. But once more it has it’s own logic to it: If electrons are magnetic monopoles it is rather logical that the photons they produce have their magnetic fields shifted by 180 degrees. It is just like in the simple complex exponential from the complex plane: e^it = cos(t) + i*sin(t). As we all know this turns counter clockwise, now if we shift the sine by 180 degrees we get cos(t) – i*sin(t) and as we all know this rotates clockwise.
This post is not meant for all the details that go into sun spots; it is more that after seven years of searching it is impossible to kill the idea that electrons are magnetic monopoles.
It is a pity that physics professors are just dumb as hell when they say that electrons are ‘tiny magnets’ without any fucking experimental proof for such bold claims. The problem those people have is that they even think it is not a problem there is no such expemental proof. So these weirdo’s build giant theoretical structures like spin waves without proving the very fundamentals of their own science.

But lets not get emotional about the giant stupidity of physics professors, they even explain the giant magneto effect in a highly complicated way and that is funny. You can’t say they are scientists, at best they are weirdo’s trying to craft a theory of everything and of course such theories are all bullshit if electron spin is not done properly.
Here is the ESO picture:

It is about time to go to the video from Lieven Vandersypen and I have an extra video also from TU Delft where they explain the Majorana fermions. Relatively early in his video Lieven claims that there “Is nothing more a quatum bit than the spin of an electron.”
Since in this post I try to explain that the only place in this universe where an electron flips it’s spin is in the head of physics professors like Lieven. It is impossible to have more contradiction as there is now between me Reinko and Lieven. In itself the video from Lieven is not that important, I only post it to show you one of those guys that believe electrons are tiny magnets while there is no experimental proof for that in the entire history of physics.

By the way in case you are interested: Lieven was the guy that years ago factored the number 15 in 3 times 5 using Shor’s algorthim. At present day we are standing at a factorization of say 21 in 3 times 7.

Back about one decade ago over there at TU Delft they thought they had found so called Majorany particles. These are particles that supposedly are there own anti-particle. That is a funny idea; if two of the same Majorana particles meet they anihilate each other. Why nature would produce such strange things is unknown to me. But if that Majorana shit is also based on electrons being ‘tiny magnets’, wouldn’t it be about time to try and prove via at least one experiment that electrons are tiny magnets?

Give me a break: university people actually using their brain?
Please get a more realistic life…

That was it for this post, once more since last year I do not try any longer to convince anybody that electrons are not tiny magnets. If the weirdo’s from Delft want tiny magnets if they look at electron behavior, what’s the problem with that?
__________
Correction and addendum from 12 Dec: In reason 2 I named it ‘fine structure’ where it should read hyperfine structure of the hydrogen spectrum. So far for the correction.
The addendum is a pdf from a 1958 article from the local university, the RUG. The old article is about spin flip in atomic hydrogen, it is about that famous 21 cm line in the hydrogen spectrum.

Now years ago when I was still very intimidated by big names like Mr. A. Einstein who had calculated the probability of a hydrogen atom to do the 21 cm transmission spontaneously. And who was I to say that electron spin was not a vector by a monopole magnetic charge and on top of that this charge was permanent just like the electric charge of an electron?

Back in time I had figured out that a collision with the right kind of electron of the right magnetic charge could also lead to this 21 cm emmision. The old electron of the hydrogen atom is simply replaced by a new one that binds in a somehow lower energy state.

To my surprise in the old article this is all covered in detail. If it is true that my idea of a permanent magnetic charge for the electron is correct, in that case 21 cm astronomy can more or less ‘see’ the galactic streams of electrons. After all if electrons are magnetic monopoles, the galactic magnetic fields play some role into what earth based astronomers see when they look at the 21 cm results.

In the next picture you can see the old text from 1958 while I use a new James Webb Space Telescope picture in the background:

Ok, left are a link to the pdf and the title of the old article:

Excitation of the Hydrogen 21-CM Line*
GEORGE B. FIELD

Link used: https://www.astro.rug.nl/~saleem/courses/EoRCourse/Field1958.pdf

Ok now I promise you I will not place more updates or corrections on this post. It’s useless anyway, if I was impressed by Einstein just think about the consequences that has for physics professors… The weirdo’s will never stop thinking that you can flip the magnetic charge of an electron. They will never stop thinking you can flip electron spin.

Till updates my dear reader.

It is no secret that over the years I have made a few rather bald predictions when it comes to magnetism. I think each and every electron is in fact a magnetic monopole and not a ‘tiny magnet’ like the professional professors think. As such I have predicted that all nuclear fusion reactors based on the magnetic confinement design will never work because if you turn such a machine on it will accelerate the electrons to crazy speeds creating tons of instability and turbulence in the plasma. And if I say ‘hey where is your experimental proof that electrons are actually magnetic dipoles’ of course nothing happens. You must never forget that all these physics professors are extremetly important persons and they will never mingle with inferior shit like people who are unemployed for almost 20 years now… No no no, we are not going to react on some crazy stuff like electrons are not magnetic dipoles. If we start doing that, the next day a homeless person will come along saying if we heal the electrons from their trauma’s you get better beer. No no no, incompetent people aren’t unemployed for no reason at all. We will neglect weirdo’s like that, after all we are the physics professors and we are on the edge of becoming masters of the universe once we have our quantum computers up and running!
I also predicted a few years back that the approach of the Delft university combined with Microsoft will not work because the Majorana particles they are based upon do not exist. It is very simple: a Majorana particle is it’s own anti particle, physics professors thought that if you combine an electron with a hole (the absense of an electron) you have a structure that is it’s own anti particle. But if you combine an electron with a hole, what mechanism is there to ensure the hole and the electron also carry opposite magnetic charges? Just like the electron and the positron carry opposite electric charges the same should go for the magnetic charges after my lazy unemployed insights.

A couple of days back when reading the news on Google news I made an internet search for ‘quantum computing’ and to my surprise there was an article from last May in the local newpaper De Volkskrant stating there was ‘bad luck’ for the heroes at Delft university. Oopsy toopsy, the Delft heroes had to withdraw an article published in Nature where the existance of Majorana particles was claimed. The fact that Nature published this bullshit in the first place is also interesting, likely the peer review mechanism works perfectly for getting the best of science into that outlet of articles. Today I checked what the publication fees are for Nature, it is only 5000€ or so (I more or less expected it to be at least 10000€) so today I learned something too… Those fees are of course a fundamental root cause as you will never find my name Reinko Venema in such overpaid shit publications. Why should I lay out 5000€ for something that will never ever pass the peer review hurdle? Since I am not an overpaid person, most of the time I try to spend my money wise.

I am sorry that the news article is in Dutch, but here is a link:
Tegenslag voor Nederlandse pionier van de quantumcomputer.

Anyway I consider this a very small success, of course the main success I am hunting for is that plasma instability in fusion reactors is caused by the acceleration of the applied magnetic fields and as such we cannot halt climate change with fusion reactors. But we have to do with overpaid university shitholes, so the waiting will be long. The combination of being overpaid while at the same time you are to stupid to ‘do the math’ often does not give a good outcome. As an example for that, look at the last financial crises that started in 2008: all those overpaid bankers and the troubles they created.

We close this post with a few pictures. The copyright of the content goes to Sam Rentmeester who likely made the photo from that extremely important Delft based physics professor:

Ok, that was it for this post. The next post is about math and we will dive into the total differential for 2D, 3D and 4D comples numbers.

This post is a continuation of the 01 May post on magnetism where we estimated that it is totally impossible that actual spinning of the electron would cause it’s magnetic properties. In the 01 May post I told you I had never seen how in physics they think electrons get accelerated in an inhomogeneous (and constant in time) magnetic fields. But when I finally tried to do some internet searching it was terrible easy to find. The offcial view is that they have an expression for the potential energy and the force is simply the gradient of the potential energy. But in order to explain the splitting in a beam in two in the Stern-Gerlach experiment something very strange has to happen: half of the electrons go into a somewhat lower energy and the other half in a somewhat higher state.

By all standards this is strange. Compare it for example to the next: You are standing on top of a building or a mountain and you start throwing rocks. Half of those rocks start falling to the ground as as such they are lowering their potential energy. The other half start flying up and as such gain potential energy like they feel anti-gravity. By all standards this is strange…

In my version of electrons where they are not magnetic dipoles but carry magnetic charge, you do not have this strange energy behavior because all electrons simply will follow their magnetic charge and as such all will go to lower energy levels.

And if the official version was true, that is half of the unpaired electrons turn into a lower energy and the other half in a higher energy spin state, that instantly brings problems when it comes to explaining permanent magnet behavior. If I grab a permanent magnet and stick it to a piece of iron, if half of the unpaired electrons would have spin up and the other half spin down, the magnet would never stick… Basically the official version of explaining the SG experiment is that you get those separation in unpaired electron spin states while when you stick a permanent magnet to a piece of iron all unpaired electrons will align to the magnetic field of the permanent magnet… That is highly contradictionary!

When just over five years back I found out the results of the SG experiment for the first time, my understanding of using an inhomogeneous magnetic field has always been that the electron feels tiny different forces with it’s north and south pole by the applied extermal magnetic field. And because the electron is so tiny, how could one unpaired electron pull an entire silver atom in two different directions?

Anyway this post is 8 pictures long, I had to made two of the a larger the rest is of the usual 550×775 pixel size.

Oh oh am I now shaking in fear because of the above photo as found on the preprint archive? If true, that would smash my idea of electrons carrying magnetic charge because if they carry magnetic charge it would not make much of a difference if the applied external magnetic field is inhomogeneous or not. A constant magnetic field simply would do.
Ok, for the time being is this the end of this post.