Monthly Archives: April 2016

Let’s kill the frustration.

April 25, 2016UncategorizedReinkoVenema

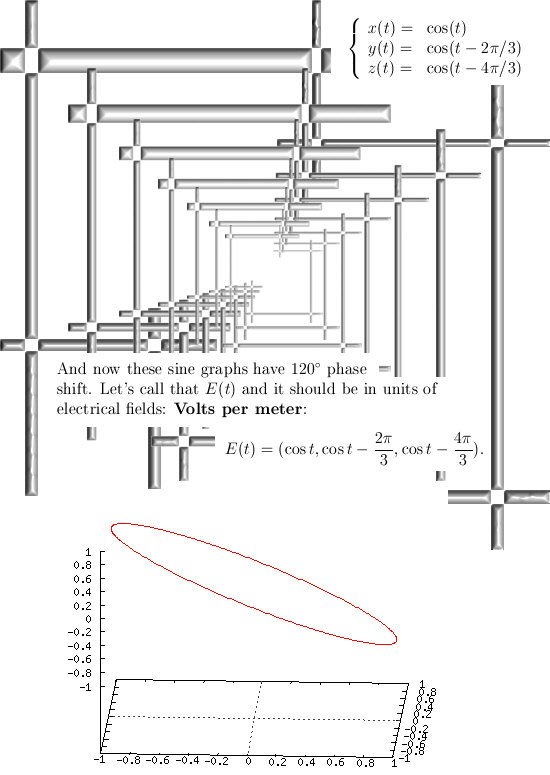
Most days I am working on a new post for the magnetics page and I am trying to put together 3 linear polarised light rays in order to get a circular polarised thing.

Since it is on the magnetics page I try to avoid all math things 3D complex numbers related.
And guess what happens? Every day I am deleting the stuff from the previous day.

This goes on for almost a week by now, but rewriting the stuff does not help much: if you do not have the right math tools, what can you do?

Now in the science of physics they can super-position two light rays in order to get a circular polarisation. I know it can also be done with three light rays but I cannot get the math on order.

On top of that, all those thousands and thousands of ‘professional professors’ get a pay rise year in year out. But the yearly payrise of these non performers is what later will be my entire yearly pension. So why should I try to explain how to combine three lightrays into a circular polarisation in the first place?

After all the professors always behave the same; there is no difference between math and physics professors, they are all skilled money parasites. And at best, perform like a ball of camel shit.

So in order to kill my own frustration, let me post an empty picture:

And after that, hang in some stupid non working math:

Ok, I feel levels of frustration in my brain declining but once more ponder the question:

Why should I carry wisdom to overpaid non-performing professors?????

__________

End of this post, till updates.

Third post on the Schrödinger wave equation using 3D complex numbers for atomic & molecular orbitals.

April 13, 20163D complex numbers, Exponential circle, Exponential curves, Matrix representation, Quantum mechanicsReinkoVenema

This update is 10 pictures long, the pictures are sized 550 by 775 pixels.
This update covers more or less everything, but I still have to explain how you find the six coordinate functions the poeple will need in order to see if these kind of complex numbers give the same result as ordinary complex numbers from the complex plane.

For those that cannot wait: In the post from 03 April I posted a teaser picture with the coordinate functions in 3D, if you multiply this against the e to the power i pi alpha thing in this update you have the six coordinate functions…

Ok ok you neatly have to write them out, but basically it is all there.

At first I was thinking it would be hard to get different results using these higher dimensional complex numbers, but when talking about atomic and molecular orbitals it might be more subtle than it looks. At the end I will post a video where some physics guy shows all kinds of orbitals related to hydrogen but his stuff is different from the pictures we observe in chemistry.
He explains this by saying that the people from chemistry always take a super-position of two wave-blobs and as such it gets oriented along the y-axis say.
If you would take super-positions of my 3D complex numbers you will get very similar results. look at the drawing in the one before last picture:
Take a super-position of an exponential circle and it’s conjugate and observe it must have the same behavior as 2D numbers from the complex plane.

(In that drawing your eys is supposed to be along the line through zero and alpha, so zero is right behind the center of the shown circle…)

Enough of the bla bla bla, here are the 10 pictures:

Click on the picture to get a larger version of the drawing:

Now finding these atomic & molecular orbitals is very hard, for simple atoms like hydrogen it is doable but what about uranium or some nice protein with only 3693 atoms in it?

All that kind of stuff falls under what we name n-body problems and for n above 3 it seems impossible to find exact analytical solutions.

There is a nice video out there explaining a bit more on the topic of finding the shapes of atomic & molecular orbitals. It is from Brant Carlson and has the title Hydrogen atom wavefunctions:

Ok, that was it for today. Till updates.

Teaser picture for the third post on the Schrödinger wave equation.

April 11, 20163D complex numbers, Exponential circle, Quantum mechanicsReinkoVenema

The stuff is more or less finished, I only have to turn it into a series of pictures so tomorrow or the day after I will post the third post on the Schrödinger equation using higher dimensional complex numbers.

Now on the other website I posted a teaser picture and since we are against cruel discrimination of peace loving websites why not post it here too?

So that is our post for today: Just a teaser picture:

Yeah yeah, once more we observe mathematical perfection.

Till updates.

Some good math for the physics community.

April 3, 20163D complex numbers, Exponential circle, Exponential curves, Quantum mechanicsReinkoVenema

Ok ok I made a relatively big blunder when sending the people from quantum mechanics using the Schödinger equation into the direction of the 3D complex numbers.

Because as a matter of fact, you cannot solve the factual Schrödinger equation in the 3D complex number system because there is no famous i to be found with the property that i^2 = -1.

You need a more advanced number system and I will explain that in detail in an upcoming post number three on the Schrödinger wave equation.

__________

In the meantime, it has not fallen on deaf ears on my side that after I posted the first Schrödinger post and I later did an internet search, suddenly with the search phrase ‘3Dcomplexnumbers’ I suddenly ended on number 1, 2 and 3.
So like expected it drew a lot of attention.

Therefore I would like to give a kind of present to the physical community because also not fallen on deaf ears, as far as I observe it physics people always try to use a product integral when they can.

Product integrals were my first serious mathematical invention, I found them while I was still trying to get my first year exam al the local university. Math professors almost never use product integrals because they are to stupid for that but physics people often put it in product integral representation.

How the history of that detail is I do not know, may be Paul Dirac had a bit to do with it…

Anyway, some time ago I wrote a pdf with the title

A tribute to Euler. Title: Ten styles for product integrals and product differentiation.
http://kinkytshirts.nl/pdfs/Product_integrals.pdf

__________

So far for the gift or the present, if you want to use other number systems beside the complex plane for depicting atomic orbitals or whatever you want to do with it, you also must know more about exponential circles and curves.

Physics people use so called ‘phase shift’ all of the time, but that is only multiplying some stuff with e to the power it or so. This is the sandpit exponential curve for toddlers.

In the world of the grown ups we have all kinds of other exponential circles and curves and guess what? I have a pdf for you with another 10 pieces of exponential circles & curves:

An overview of exponential circles and curves.
http://kinkytshirts.nl/pdfs/10_exponential_circles_and_curves.pdf

A possible way of parametrization of 3D exponential circles is given in the next picture and understanding this stuff is important when it comes to the third post related to the Schrödinger equation:

This is the end of this intro to the third Schrödinger post.
Have a nice life or try to get one.

Till updates.

Schrödinger wave equation part 2.

April 1, 20163D complex numbers, Laplacian, Quantum mechanicsReinkoVenema

A few posts back I wrote a bit about the Schrödinger wave equation related to calculating atomic and molecular orbitals for electrons using 3D complex numbers.

What I said was basically correct but also an over-simplification of the situation.
The problem is very very basic: in the 3D number system, let it be complex or circular, you just cannot solve and equation like $X^2 = -1$.
Hence the number i from the complex plane with i^2 = -1 just does not live in 3D real space.

So using alternative number systems outside the complex plane is not a straightforward thing to do, yet in principle all higher dimensional complex numbers should give the same results.
If not there would be a very basic problem inside the wave equation from quantum mechanics and I am not aware of any faults in that detail of the quantum theory.

Here are two pictures that serve as an addendum on the previous post on the Schrödinger equation:

Now if you are reading this it is very likely that at least once in your life you have seen a solution to the Schrödinger wave equation like the ‘particle in a box’. And that is not a 3D box but the one dimensional box or just an interval of the real line.

Solving the Schródinger stuff for atomic and molecular orbitals is a very different kind of game; these are always many particle systems where every particle influences the system and the entire system influence the individual particles.
Mathematically speaking it is a nightmare; analytical solutions are not possible they say.
It can only be solved numerically…

__________

But keep on dreaming, after all they also say decade in decade out that electrons are magnetic dipoles. There is no experimental proof for that only theoretical bla bla bla.

Let’s leave it with that. Till updates.