What the hydrogen bomb is in the average nuclear arsenal, that is what modified Dirichlet kernels are for higher dimensional complex & circular number systems.
Via the so called tau calculus I was able to achieve results in 3 and 5 dimensional number systems and I really had no hope in making more progress in that way because it gets so extremely hardcore that all hope was lost.
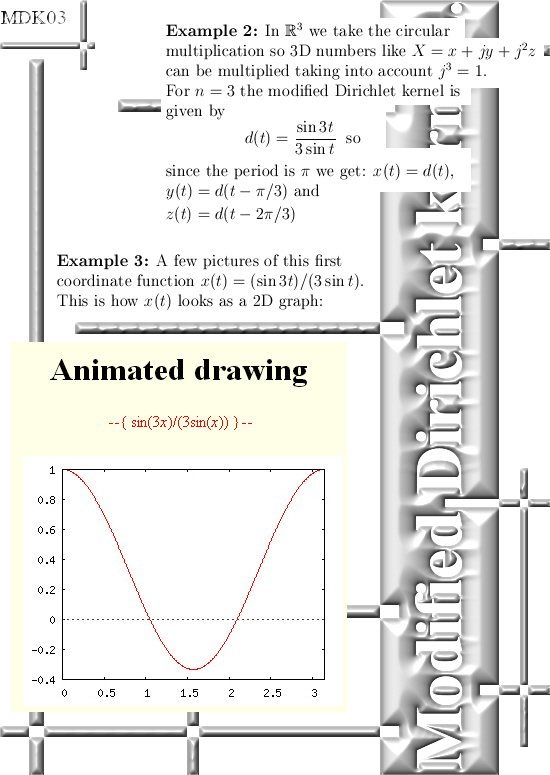
Yet about two years ago I discovered a very neat, clean and very beautiful formula that is strongly related to the Dirichlet kernel known from Fourier analysis. The formula I found was a dressed down version of the original Dirichlet kernel therefore I named it ‘modified Dirichlet kernel’.
This modified kernel is your basic coordinate function, depending on the dimension of the space you are working in you make some time lags and voila: There is your parametrization of your higher dimensional exponential (periodic) curve (only in 2D and 3D space it is a circle).
For myself speaking: this result of finding the modified Dirichlet kernel is for sure in my own top 10 list of most important results found. Not often do I mention other mathematicians, but I would like to mention the name of Floris Takens and without knowing how Floris thought about taking a sample of a time series and after that craft time lags on that, rather likely I would not have found this suburb and very beautiful math…
__________
I haven’t decided what the next post will be about.
It could be stuff like:
- How I found the first modified Dirichlet kernel, or
- Wirtinger derivatives for 3D number systems, or
- Wow man, can you factorize the Laplacian operator form Quantum Mechanics???
But factoring the Laplacian requires understanding 3D Wirtinger derivatives so likely I will show you how I found the very first modified Dirichlet kernel.
__________
This update contains six jpg pictures each about 550 x 775 pixels and two old fashioned animated gif pictures. I tried to keep the math as simple as possible and by doing that I learned some nice lessons myself… Here we go:
This is the animated gif using z = 0 in 3D while this picture is showing the Euler exponential circle:
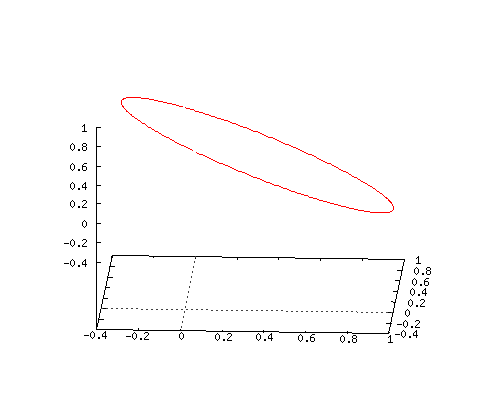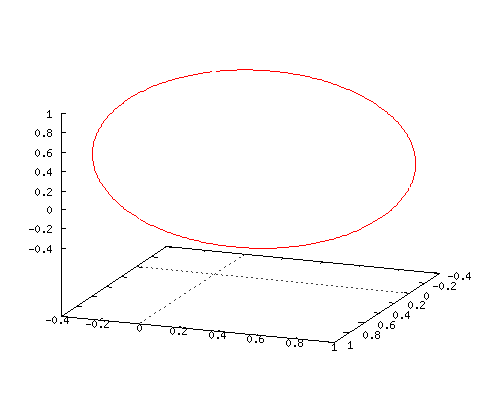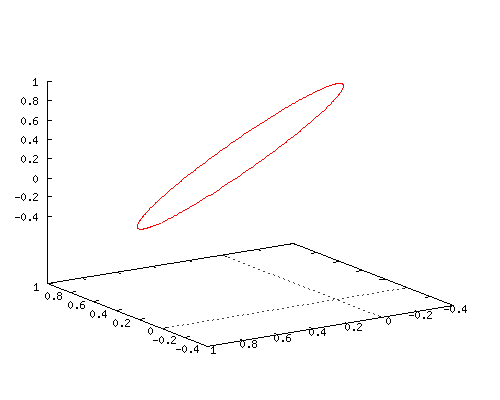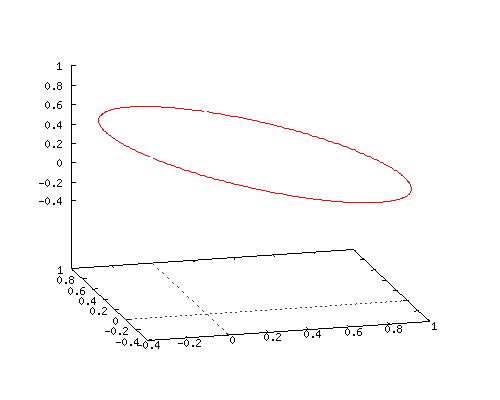
Here is an animated gif of how this coordinate function looks when you combine it with the two time lags for the y(t) and z(t) coordinates. Does it surprise you that you get a flat circle?
If it does not surprise you, you do not understand how much math is missing in our human world…
In case you are interested in the ‘time lag’ idea as Floris used it, here is a nice Youtube video that gives a perfect explanation. If you apply this time lag idea for example is a 17 dimensional real vector space you get a 17D exponential curve with all of it’s magnificent properties…
Takens’ theorem in action for the Lorenz chaotic attractor
Yes, end of this post. See ya around & have a nice life or try to get one.