Originally I planned to upload tonight the new post on the integrals related to the number tau for the circular multiplication. But I found this very cute result from some other math professors, I believe these are two brothers Borwein & Borwein.

Beside that I also had more time to spend on a very important hobby: Brewing beer…;)

Four years back when I for the first time derived integrals like this with the cosine and sine stuff to the power three in it, I just had no clue whatsoever how to find analytical stuff for their value. These kind of integrals cannot be solved by throwing in some simple primitive or so.

At present I have two independent proofs for their value.
Back in the time I knew there was some internet website that contains a whole lot of integer sequences so if I could find that I would have at least some analytical clue about that nasty problem. Only a long time later I found that website, but is said ‘we do not know’.
Or ‘unknown integer sequence’ or whatever what.

But yesterday when I tried more or less to get a negative result my luck changed for the better: the website with the integer sequences in it actually returned an answer.

And for my few pounds of human brain tissue the answer was completely crazy.
Therefore I decided to put the result of this Borwein function on top in the teaser picture and my own idea’s at the bottom. Here it is:

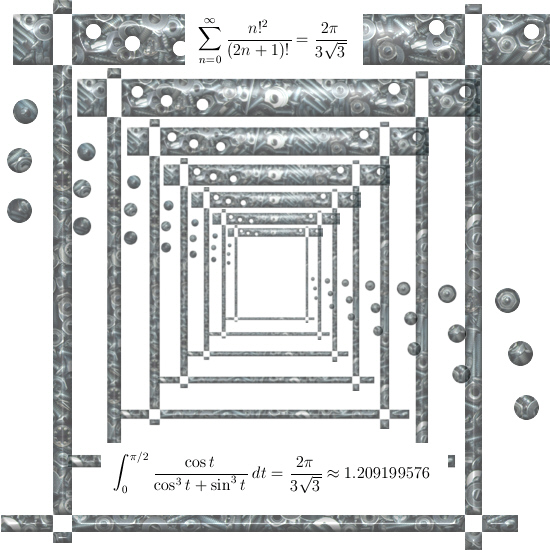I have absolutely no clue as why these two things should be the same, but four years back I had absolutely no clue as what this numerical value like 1.2092 actually meant…

The link to what might be the Borwein & Borwein function

A248897 Decimal expansion of Sum_{i >= 0} (i!)^2/(2*i+1)!.
https://oeis.org/A248897

Let’s leave it with that, see ya in the next post.