In the previous post we had some stuff on the pull back map but also those links to complicated theorems. Therefore I tried to explain the inner workings of the pull back map that pull higher dimensional complex & circular numbers back to the complex plane in as easy to understand chunks as I could.

In the next post I only use advanced high school math (for my own country that would be the VWO education line, the classes 5 and 6) and for the rest any university student that has followed an elementary crash course on the complex plane.

I am very glad I could find such simple ways to pull back higher dimensional exponential circles and curves back to that goodie good old Euler formula that says stuff like e^it is related to the cosine and the sine functions.

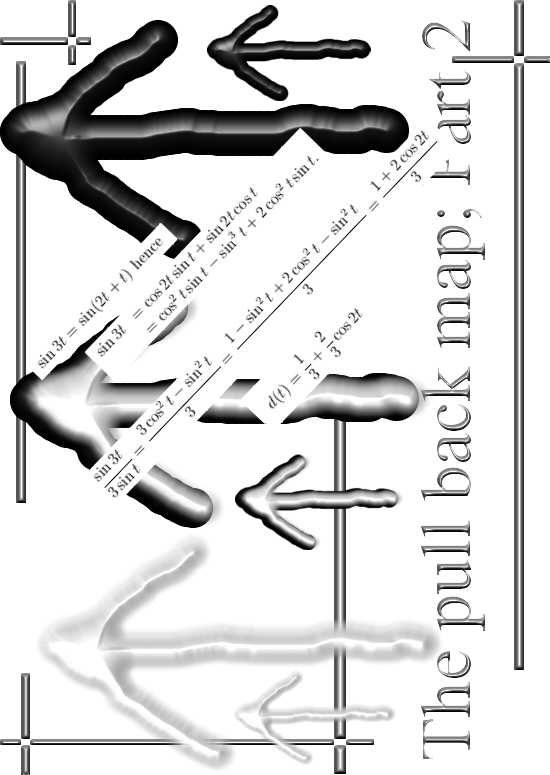
All stuff is boiled down to things you can see in the teaser picture below, no new advanced 20th century math ideas, only using century old well known trigonometric equations and that is all…

Once more: Higher dimensional complex number systems are just there, it is a natural thing like the natural numbers like 1, 2, 3,  4, 5 etc are. Where the complex plane is something like a fish bowl, the higher dimensional complex & circular numbers are a big ocean.
But if you as a so called professional math professor can only swim your circles inside the fish bowl, can you survive the currents in this giant ocean?

No of course you can’t, so good luck with your future life inside the complex plane.

After this blah blah blah (remark the math professors are also extremely smart if you look at how much salary they suck in let alone the ‘research money’ they get to form global research groups that use at best two dimensional complex numbers) it is time for the teaser picture:

At last I would like to remark that the pull back map is on equal footage with the modified Dirichtlet kernels for my individual emotional system; I am glad I am still alive and can find stuff like this.

Till updates.