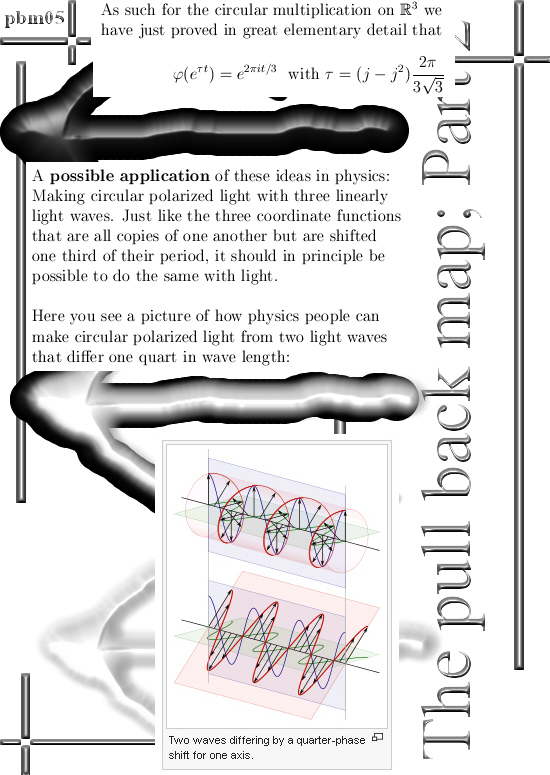
In this post, number 50 by the way, I am trying to use as elementary math as possible in order to use the pull back map from the 3D circular number system to the complex plane.

With this the pull back map and the 3D circular number system are treated so basic that with only high school math and a crash course in the complex plane students can understand what I am doing.

So for reading this post number 50, what do you need in mathematical knowledge?
1) Understand how to write cos(a + b) and sin(a + b) in terms of cos a and sin b.
2) Understanding of e to the power it in terms of cos t and isin t.
3) Understanding of the roots of unity as found inside the complex plane, in particular being able to calculate all three roots of unity when we take the third root of the number 1.

That’s all, so basically all first year students in math, physics and chemistry could understand this post at the end of their first year on a local university.

__________

The words above are only one reason to write this post; to be honest for me it took a long time to write down for the first time the coordinate functions for the 3D exponential circle.

And I never did give much solid proof for that these coordinate functions have indeed the properties as described. It all more or less came out of the sleeve as some kind of monkey trick.

Therefore for myself speaking, this post giving the results in it also serves as a proof that indeed there is only one class of coordinate functions that do the job. They can only differ in the period in time they need to go around, if you leave that out the triple of coordinate functions becomes unique.

All in all the goals of this post number 50 are:

1) To do the pull back of an exponential circle as simple as possible while
2) In doing so give some more proof that was skipped years ago.

__________

This update is seven pictures long, each 550 x 775 pixels in size.
Hit the road Jack:

I think I have nothing more to say, so see you around my dear reader in post number 51.

Till updates.