This is the 91-th post on this website so surely but slowly this website is growing on. This post was more or less written just for myself; I don’t know if the concept of Wirtinger derivates is used a lot in standard complex analysis but I sure like it so that’s why we take a look at it.

The idea of a Wirtinger derivative is very simple to understand: You have some function f(Z) and by differentiating it in the direction of all four basis vectors you craft the derivative f'(Z) from that.

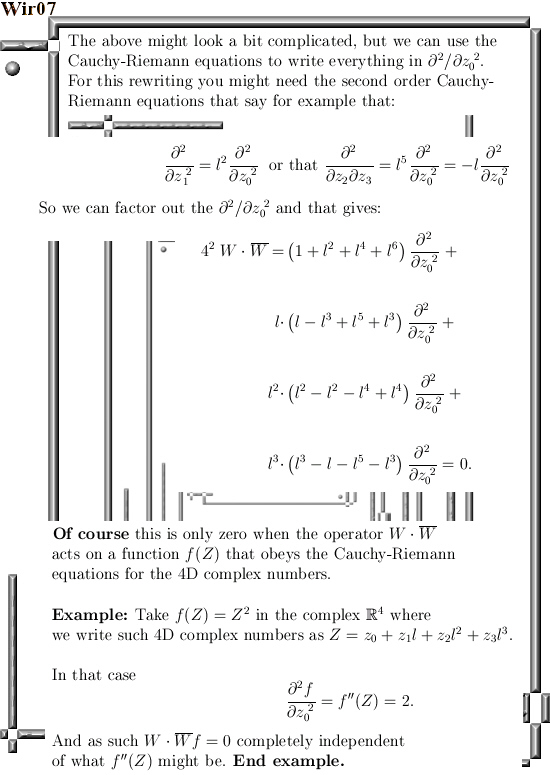
At the basis for all the calculations we do in this post are the Cauchy-Riemann equations that allow you to rewrite the partial derivatives we put into the Wirtinger derivative.

The main result in this post is as follows:
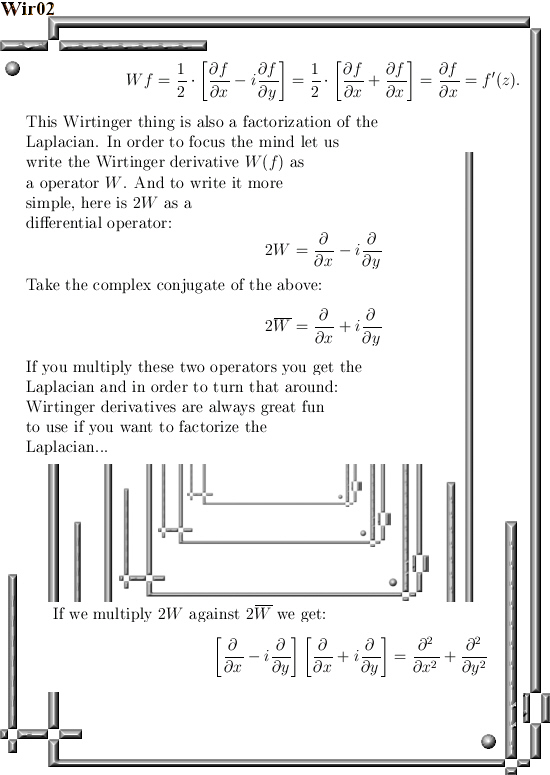
We take our Wirtinger operator W and we multiply it with the 4D complex conjugate of W and we show that this is a real multiple of the Laplacian.

The 4D case is more or less the same as on the complex plane, that is not a miracle because in previous 4D basics we already observed two planes inside the 4D complex numbers that are isomorphic to the complex plane. So it is not much of a surprise the entire 4D space of complex numbers behaves in that way too; all functions are harmonic that is the Laplacian of such a function is zero.

This post is ten pictures long, most of them are size 550 x 775 but a few of them are a bit broader like 600 x 775 because the calculations are rather wide.

On the scale of things this post is not ultra important or so, it is more like I wrote it for myself and I wanted to look in how much this all was different from the three dimensional case.

Here are the pics:

Further reading from a wiki (of course that is only about 2D complex numbers from the complex plane):
Wirtinger derivatives
https://en.wikipedia.org/wiki/Wirtinger_derivatives

Ok, that was it. Till updates.