This is a short and simple update that nicely fits into the series of the basics of 4D complex numbers. It is only 3 pictures long and all we do is multiply a 4D complex number A by one of the imitators of i and after that calculate the inner product between A and A times the imitator of i.

Compare it to the complex plane: Take a 2D complex number z from the complex plane, write it as a vector and also write iz as a vector. Take the inner product and conclude that it is zero so that z and iz are perpendicular to each other.

That’s all we do in the space of 4D complex numbers:

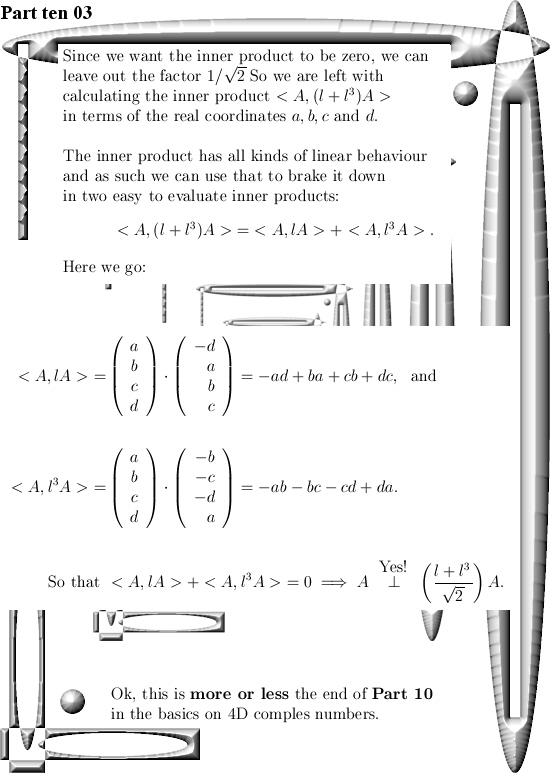
I hope this was basic enough…  See you in the next post.