Monthly Archives: November 2018

Do lunatics rule the asylum called physics?

Magnetism

There is a Youtube channel named the science asylum. It is run by a guy that makes your head tired but for a few minutes it is often nice to watch. In the next video he tries to explain magnetism, both electro-magnetism and permanent magnets.

Here is the video:

The video guy tries to explain permanent magnets via the concept of angular momentum. As far as I know physics now this is indeed the way it has historically evolved. Now a lot of physics folks think that the unpaired electrons somehow go around the nucleus and as such create a magnetic dipole moment, other place more emphasis on electrons being the basic dipole magnets and if they align all conditions for possible permanent magnets are there. Of course beside electrons also the so called magnetic domains need to align and the official version is that this is more or less the way some materials like iron can be turned into permanent magnets.

In my view there is a long list of problems that come with that. For example the Curie temperature, above the Curie temperature the permanent magnet looses it’s magnetism completely.

If you view electrons as magnetic monopoles, stuff like the Curie temperature become a lot more logical: above the Curie temperature it has to be that the metal is so hot it starts to loose it’s unpaired electrons.

In my view, when permanent magnets are manufactured it is the applied external magnetic field and the slow slow cooling down from above the Curie temperature that ensures the magnet becomes ‘permanent’.

There should be a simple experimental proof for that but although for years I tried to find it, until now I still haven’t found it. But in our global industrie a lof of permanent magnets are made every day and the experimental proof for my view on electron spin simply says the next:

If during the cooling down a NS external magnetic field is applied, the permanent magnet will come out as a SN magnet.

With SN I simply mean that the magnetic south pole is on the left while the magnetic north pole is on the right. So the macroscopic object known as the permanent magnet will always be anti-aligned with the magnetic field that is applied during the fabrication of the permanent magnet.

I still haven’t found it after all these years, but if it comes out that permanent magnets have the same orientation as the applied external magnetic field during fabrication, I can trash my theory of magnetic charges and finally go on with my life…

But there are plenty of problems more with the standard model version of electrons being magnetic dipoles. Here is a screen shot from 4.35 minutes into the video from the crazy asylum guy and it contains so called quantum numbers.

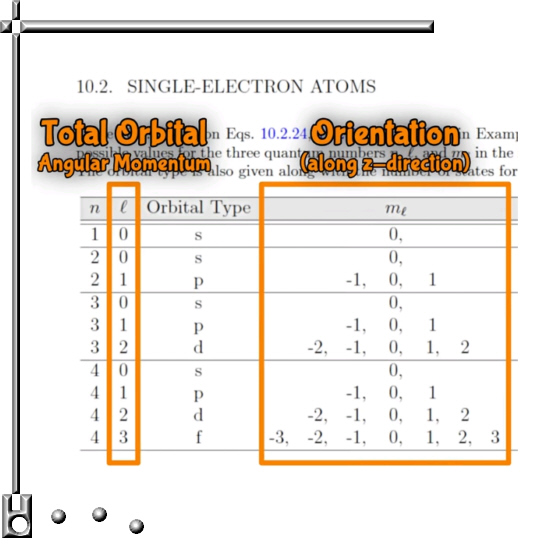
The title in the picture might look a bit confusing because the only single-electron atom in the universe is the hydrogen atom. Likely the author means the number of unpaired electrons in some atom.

You observe two quantum numbers that are holy inside quantum mechanics:
The so called ‘Total orbital angular momentum’ number l and something weird because it is only along the z-axis direction m_l.

In my view, if electrons carry magnetic charge and are not magnetic dipoles and for example it has 3 unpaired electrons, total magnetic charge runs from -3 to +3.

And that is precisely what the m subscript l number does…

So I still have to find the very first fault in my simple idea that electrons just carry one of the two possible magnetic charges.

In this post I skipped the fourth quantum number: total spin. That is also a quantum number thing so is it a vector (a magnetic dipole) or a magnetic charge (a magnetic monopole)?

Ok, let’s leave it with that. Have a nice set of quantum numbers or try to get one.

Added on 26 Nov:

May be looking at chaotic guys makes me chaotic too, but reading back what I wrote yesterday I think it is better to explain the ‘anti alignment’ a bit more because I explained it far too confusing I just guess.

I made a schematic sketch of it, you see two coils that make a long lasting constant magnetic field and in that field a hot piece of iron is slowly cooling down. An important feature of iron is that the four unpaired electrons are in the inner shells, this is a consequence of the so called aufbau principle.

Here is the sketch:

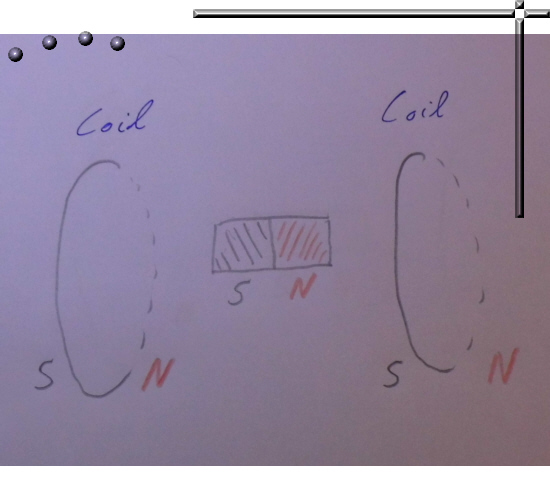
So my basic idea of manufacturing permanent magnets is the fact that during the long cool down the unpaired electrons can settle in those inner shells inside the electron could of the iron atoms.

Furthermore it has to be that the chrystal structure metals like iron make is such that the individual iron atoms cannot rotate. It is fixed in place. And with the unpaired magnetic charge carrying electrons in place after the long cool down, that is why your permanent magnet is more or less permanent:

Small surplusses of south charged electrons should be at the left & vice versa a bit more north magnetic charge at the right as sketched above.

This all sounds very simple but we also have those magnetic domains in metals like iron, those magnetic domains are just small surplusses of either one of the two magnetic charges. This blurs the simplicity a bit but it perfectly explains as why unmagnetized iron gets attracted to magnets anyway: the dynamics of the magnetic domain changes under the influence of the outside permanent magnet…

At last I want to remark that if the idea of permanent magnetism would solely based on dipole electron spin that aligns, in that case strong permanent magnets should change the permanent magnetism of weakly magnetized iron. The strong magnets would simply eat up the electrons of the weak permanent magnet.

That just does not happen. Last spring I made a small toungue in cheek ‘experiment’ with that where I placed my stack of most strong neodymium magnets against two of my most weak magnets. It was all fixed in place over 24 hours, but after all that time my two most weak permanent magnets exposed the same behaviour as before.

So no electron was flipped and for me that was one more reason to say farewell to the idea of electrons being magnetic monopoles.

Here is a link to that very simple toungue in cheek experiment, I hope it is so simple that physics professors will vomit on that…

08 March 2018: Reason 56: This experiment shows zero spin torque transfer.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff03.htm#08March2018

Ok, I have to stop this post because it is over 1100 words long and that is far beyond the attention span of professional physics professors.

Have a nice set of parallel universes while not even understand permanent magnets or try to get even more beautiful parallel universes…

Till updates my dear reader.

Calculation of the 4D number tau diagonal matrix style.

4D complex numbers, Exponential curves, Matrix representation

In the begin of this series on basic and elementary calculations you can do with 4D complex numbers we already found what the number tau is. We used stuff like the pull back map… But you can do it also with the method from the previous post about how to find the matrix representation for any 4D complex number Z given the eigenvalues.

Finding the correct eigenvalues for tau is rather subtle, you must respect the behavior of the logarithm function in higher dimensions. It is not as easy as on the real line where you simply have log ab = log a + log b for positive reals a and b.

But let me keep this post short and stop all the blah blah.

Just two nice pictures is all to do the calculation of the 4D complex number tau:

 

(Oops, two days later I repaired a silly typo where I did forget one minus sign. It was just a dumb typo that likely did not lead to much confusion. So I will not take it in the ‘Corrections’ categorie on this website that I use for more or less more significant repairs…)

Ok, that was it.

Diagonal matrices for all 4D complex numbers.

4D complex numbers, Exponential curves, Matrix representation

This website is now about 3 years old, the first post was on 14 Nov 2015 and today I hang in with post number 100. That is a nice round number and this post is part 15 in the series known as the Basics for 4D complex numbers.

We are going to diagonalize all those matrix representations M(Z) we have for all 4D complex numbers Z. As a reader you are supposed to know what diagonalization of a matrix actually is, that is in most linear algebra courses so it is widely spread knowledge in the population.

Now at the end of this nine pictures long post you can find how you can calculate the matrix representation for M(l) where l is the first imaginary unit in the 4D complex number system. And I understand that people will ask full of bewilderment, why do this in such a difficult way? That is a good question, but look a bit of the first parts where I gave some examples about how to calculate the number tau that was defined as log l. And one way of doing that was using the pull back map but with matrix diagonalization you have a general method that works in all dimensions.

Beside that this is an all inclusive approach when it comes to the dimension, in practice you can rely on internet applets that use commonly known linear algebra. Now if you are a computer programmer you can automate the process of diagonalization of a matrix. I am very bad in writing computer programs, but if you can write code in an environment where you can do symbolic calculus in your code, it would be handy if that is on such a level you can use the so called roots of unity from the complex plane. After all the eigenvalues you encounter in the 4D complex number system are always based on these roots of unity and the eigenvectors are too…

This post number 100 is 9 pictures long, as usual picture size is 550 x 775 pixels.
In the next post number 101 we will use this method to calculate the matrix representation of the number tau (that is the log of the first imaginary unit l).

Ok, here are the pictures:

That´s it, in the next post we go further with the number tau and from the eigenvalues of tau calculate the matrix representation. So see you around.