This evening I brewed a fresh batch of wort, it is now cooling and tomorrow when it is at room temperature it can go into the fermenter bottles. Everything is relaxed around here, in the last week in my city only four cases of COVID-19 into the hospital.

Orginally I planned to define the 4D way of taking a Fourier series in this post, but while writing this post I realized to would become too long. So this post is seven pictures long (all 550×775 pixels) therefore I hope it does not cross the length of your attention span. For myself speaking always when I read some stuff that is ‘too long’ I start scrolling till the end and as such you often miss a lot of important details.

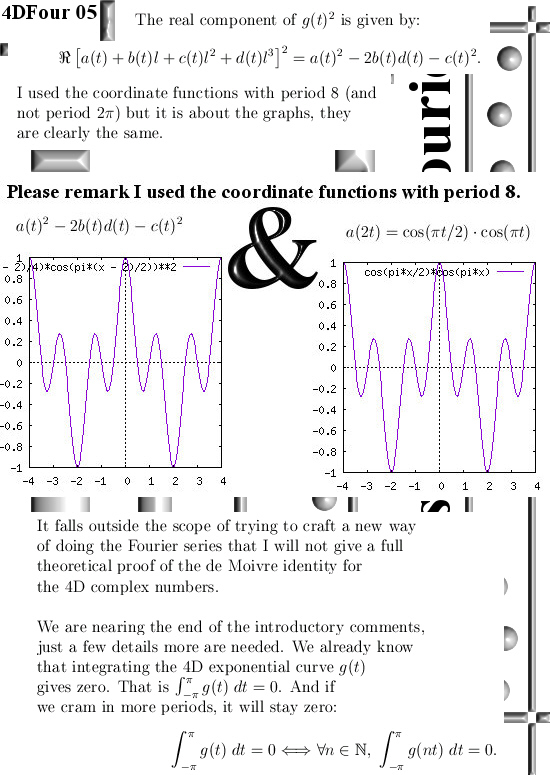
An important feature of exponential curves is that you have those de Moivre identities that come along with all those exponential curves. In this post I did not prove the 4D version of a de Moivre identity for the 4D complex numbers, but I give some numerical evdence. It has to be remarked that when I wrote the 20 posts around the basics of the 4D complex number system, I did not include the de Moivre identity. So that is more or less an ommision. On the other hand it is of course much more important to be able to find the exponential curve in the 4D space that is the basic material needed to write down such a de Moivre identity.

I categorize these posts about the 4D Fourier series also under ‘integration’. Not that I have many fantastic insights about integration but the reason for this category is much more down to earth: You have to perform an integration for every Fourier coefficient you calculate. In case you missed it: this year I finally wrote that post about how to define integration in the 3D complex numbers. Use the search function of this website in order to find that post in case you are interested.

Ok, that is what I had to say. Let us go to the beef of this post number 153 and that is of course the seven pictures that are all hungry for your attention. Here are the seven pictures:

There is an online Fourier series applet as it is named in these years. In the past we did not have applets but only computer programs. Anyway it is important those applets are there so I want to give a big thumbs up to the people that maintain that website! Here is a link to the Fourier thing:

Fourier series calculator. Link used: https://www.symbolab.com/solver/fourier-series-calculator

At last I want to point at the importance of such free websites. It is very good if a society has enough of this kind of ‘free stuff’. For example when in the year 2012 I picked up my study of the 3D complex numbers for me it was very important that there were free online applets for the logarithm of a matrix. Without such a free website I would have taken me many more years to find those exponential circles & curves. Or I would not have found them at all because after all my biggest breakthrough was when I did read that numerical evidence from log j on the 3D complex numbers: why are the two imaginary components equal I was just wondering? Later I found how crucial that was: only if the imaginary components are equal the eigenvalues are purely imaginary in the complex plane.

So I am breaking a lance for free websites where you can find good applets (read: computer programs) that help your understanding of math.

Ok, that’s it for this post. In the next post I will finally give that definition and after that I do not have a clue. I still do not have any good proof for convergence of these 4D Fourier series so we’ll see. Till updates.