After a few weeks it is finally dawning on me that it might very well be possible that the professional math people just do not have a clue about how easy it is to find counter examples to the FLT. (FLT = Fermat’s Last Theorem.) That is hard to digest because it is so utterly simple to do and understand on those rings of integers modulo n.
But I did not search long and deep and I skipped places like the preprint archive and only used a bit of the Google thing. And if you use the Google thing of course you get more results from extravert people. That skews the results of course because for extraverts talking is much more important compared to the content of what you are talking or communicating. That is the problem with extraverts; they might be highly social but they pay a severe price for that: their thinking will always be shallow and never some stuff deeply thought through…

As far as I know rings of the integers modulo n are not studied very much. Of course the additive groups modulo n are studied and the multiplicative groups modulo n are studied but when it comes to rings all of a sudden it is silent always everywhere. And now I am looking at it myself I am surprised how much similarity there is between those kind of rings and the 3D complex & circular numbers. Of course they are very different objects of study but you can all chop them in two parts: The numbers that are invertible versus the set of non-invertibles. For example in the ring of integers modulo 15 the prime factors of 15 are 3 and 5. And those prime factors are the non-invertibles inside this ring. This has all kinds of interesting math results, for example take the (exponential) orbit of 3. That is the sequence of powers of 3 like in: 3, 3^2 = 9, 3^3 = 27 = 12 (mod 15), 3^4 = 36 = 6 (mod 15) and 3^5 = 18 = 3. As you see this orbit avoids the number 1 because if it would pass through 1 you would have found an inverse of 3 inside our ring and that is not possible because 3 is a non invertible number…

Likely my next post will be about such stuff, I am still a bit hesitant about it because it is all so utterly simple but you must never underestimate how dumb the overpaid math professors can be: Just neglecting rings modulo n could very well be a common thing over there while in the meantime they try to act as a high IQ person by stating ‘We are doing the Langlands program’ & and more of that advanced blah blah blah.
Anyway it is getting late at night so from all that nonsense weird stuff you can find on Google by searching for counter examples to the last theorem of Fermat I crafted 3 pictures. Here is the first one:

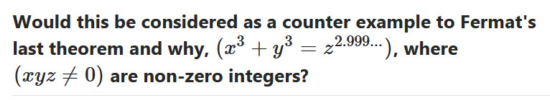
I found this retarded question on quora. For me it is hard to process what the person asking this question was actually thinking. Why would the 2.999…. be important? What is this person thinking? Does he have integer solutions to say 2.9 and 2.99 and is this person wondering what would happen if you apply those integer solutions to 2.99999999…..???????

It is retarded, or shallow, on all levels possible. So to honor the math skills of the average human let’s make a new picture of this nonsense:

We will never be intimidated by the stupidity of such questions and simply observe these are our fellow human beings. And if ok, if you are a human being running into tons of problems, in the end you can always wonder ‘Am I a problem myself because I am so stupid?’

If you have figured out that question, you are getting more solid & you look more like a little cube:

I want to end this post on a positive note: Once you understand how stupid humans are you must not view that as a negative. On the contrary, that shows there is room for improvement.