To be honest this post is not carefully thought through. I felt like starting to write and at first I wanted to write it more into the direction of a proof based on the volumes of the parallelepiped and it’s expansion columns. But then I realized that my cute calculating scheme of turning a nxd matrix A into a square nxn matrix AP could go wrong. So I wanted to address that detail too but I hadn’t thought it out enough.
The answer to why it can go wrong is rather beautiful: Take any nxd matrix (of course the number of columns cannot exceed n because that is not a proper d-dimensional parallelepiped) say a 10×3 matrix. The three columns span a parallelepiped in 10-dimensional real space.
The ‘smallest’ parallelepiped that still has a three dimensional volume is one of the many minors possible in the 10×3 matrix. So with ‘smallest’ I mean the parallelepiped that uses the least number of coordinates in our 10-dimensional space.
Now in my calculating scheme, an algorithm if you want, I said you to start at the top of the matrix A and add more and more columns. But if A is made of just one 3×3 minor, say at the bottom of A, it is crystal clear my calculating scheme goes wrong because it now produces only zero columns.
And if that happens, when in the end you take the determinant of the square matix AP you get zero and of course that is wrong. These are exceptional cases, but it has to be addressed.
Of course there is no important reason for the calculation scheme to start at the top of the matrix, just start at the position of the lone 3×3 minor. In general: If you start with a nxd matrix, ensure your first expansion column is not a zero column. After that the next expansions all should go fine.
This post is five pictures long. If you haven’t mastered the calculation scheme of how to turn a non-square matrix into a square matrix you must first look up previous posts until you have a more or less clear mental picture of what is going on with this.

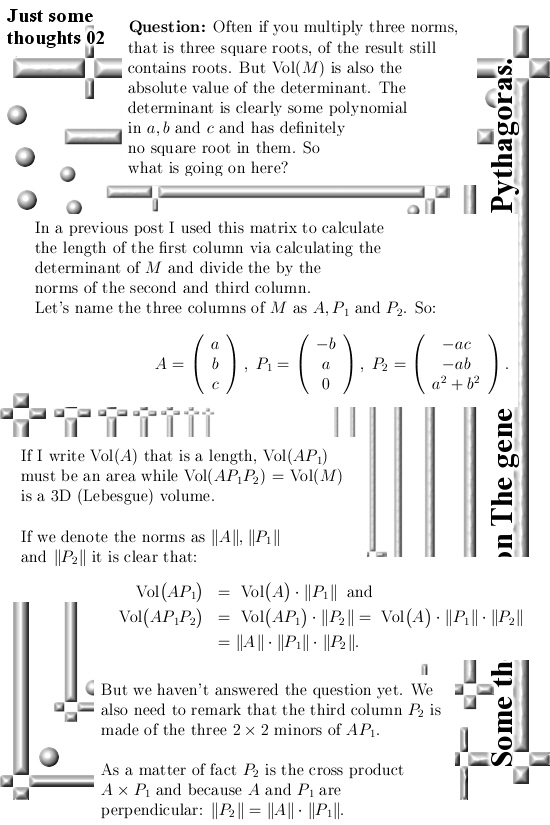


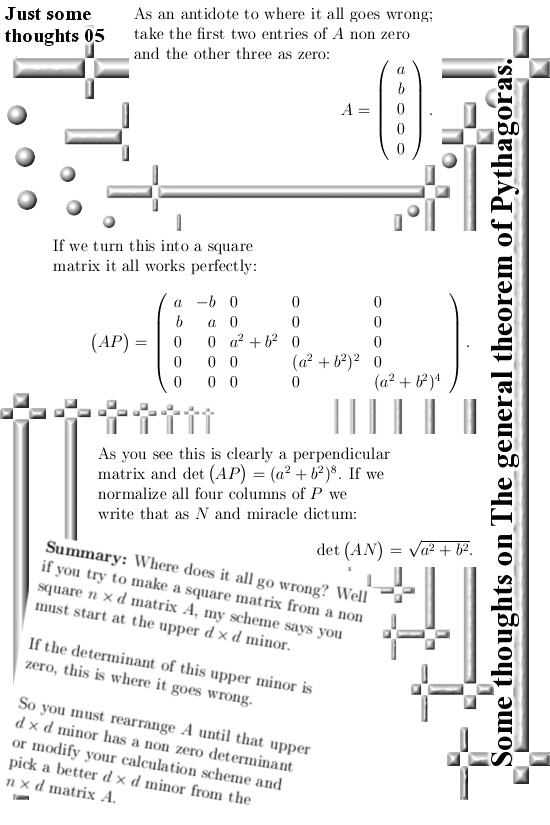
Ok, that was it for this post on the highly beautiful calculation scheme for the volumes of parallelepipeda in higher dimensions.