Lately I added a bunch of sine functions and I wondered what the maximum was. And to be honest I had no idea, in math that is pretty normal otherwise you would not search for such answers. The questions you can answer instantly are often much more boring and often don’t add much value or insights. So what was I looking at?
Well take the sine function, lets write it as sin(t). Make a timelag of one unit or if you want a translation and that’s sin(t – 1). Proceed in taking time lags like sin(t – 2), sin(t – 3) and so on and so on and add them all up.
The question is: Can you say something about the maximum value that this sum can take? And no, I had no idea about how to approach this problem.

The interesting detail is of course that this sum of sines does not seem to converge or diverge in any significant way. You can check that for yourself in for example the DESMOS package, just type the word sum and you get the sigma symbol for a summation. I like the package and in case you have never seen it, here is a link: https://www.desmos.com/calculator?lang=en.

As far as I know this problem has no or little math meaning, it is just some recreational stuff. But if you in your life had the honor of calculating a bunch of Fourier coefficients again and again, you know that the summation of sines and or cosines and or complex exponentials can have very tricky convergence questions. Now with my little sum of sine time lags we don’t have any convergence at all, the funny thing is it also does not diverge.

This post was meant to be short but as so often it grew to five pictures long and on top of that there are three extra figures added to the mix. It’s all pretty simple and not deep complicated math that as so often is very hard for human brains to digest. Have fun reading it.

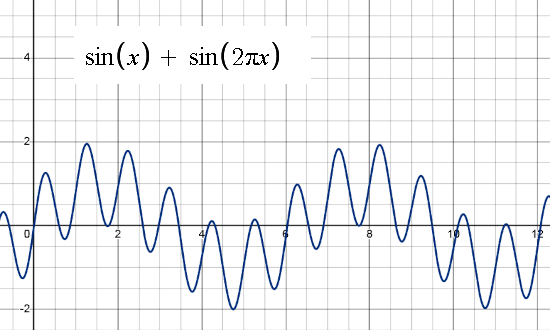
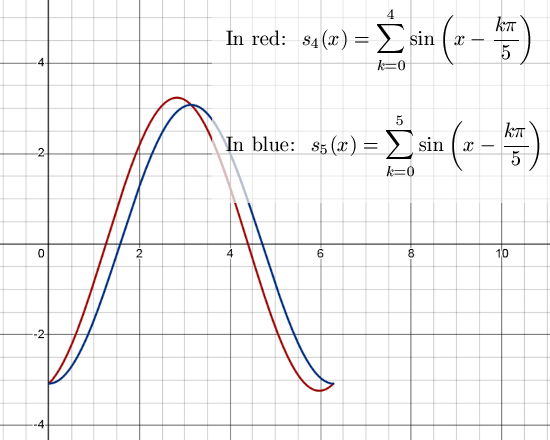
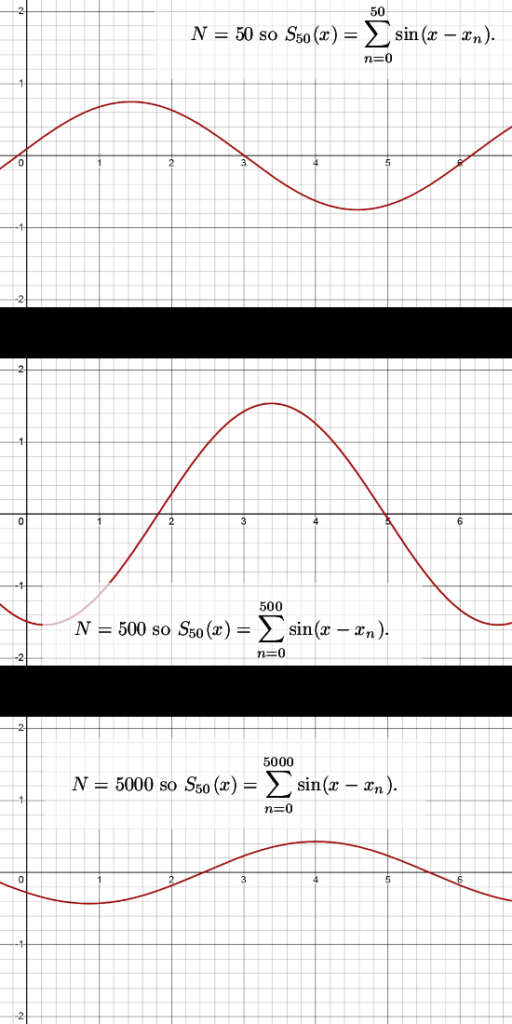
At the end of this post I want to remark that I framed the question for some finite sum of sines. That is because I wanted to avoid all things related to taking a supremum and stuff like that. Look at Example 1 above, here of course the maximum value of the two sines is not 2 because there is no real solution to this, but of course the supremum is 2 because you can come arbitrarily close to 2.
Of course in Example 3 I wanted to know the sup and the inf of the amplitudes, but I framed the question in a finite sum of sines anyway.

Ok that was it for this unclassified post. If you want you can think a bit about sums of sines and if you get bored of that you can try to figure out what an electron pair is if the Pauli exclusion principle says it must have opposite spins… Thanks for your attention and see you in the next post.