If you view the interger points of the plane equipped with the elliptic complex multiplication as prime numbers or composites, you have found a good basis to predict or calculate how much of such integer solutions there are. This problem is closely related to the number of integer points on a circle, I am sure you can find enough internet resources of that problem.
I decided to take a deeper look into this because of a video on the Eisenstein primes, those Eisenstein primes and integers look a lot like my own elliptic complex integers. But the Eisenstein numbers are defined on the standard complex plane while I modified the way the multiplication is done via a tiny change to i^2 = -1 + i. So that now ‘rules’ my plane with elliptic complex numbers and one of the nice properties is that i^3 = -1 while for that Eisenstein stuff you get +1. So the Eisenstein numbers are more a way of say the split complex numbers.
Lets start with the video that I considered to be remarkable good:

For me it was all brand new because to be honest I never ever studied the Gaussian integers and how that gives rise to a unique way of factorizing them. But now I had to solve the problem for my own 2D elliptic numbers I have to say that yes it is beautiful once you grasp what’s going on.

A well known fact from the Gaussian integers is that the number 5 is now no longer a prime number because it can be factored into 2 + i and 2 – i. On the complex elliptic numbers it is 7 that is the smallest integer to have that same fate as 5 on the Gaussian integers. This post is mostly about the two factors that factorize 7, I named them p and q and the interesting thing is they are each others conjugate.
But the number 3 is also no longer a prime so all in all for a person like me who dislikes algebra so often for so many years, it was all in all a nice patch of math to understand.

This post is 8 pictures long, each 550×1250 pixels and on top of that two extra figures are addes. So what more do you want? I kept the stuff as less technical as possible while hoping that if you want to dig a bit deeper you can do that for yourself now. So lets start the picture thing:

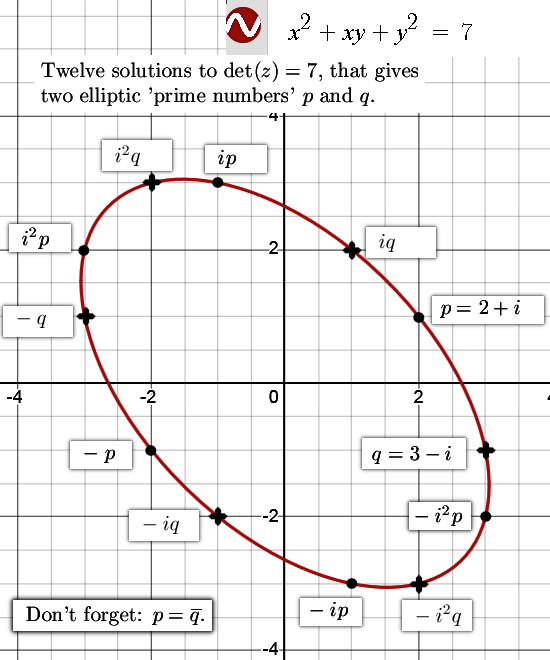
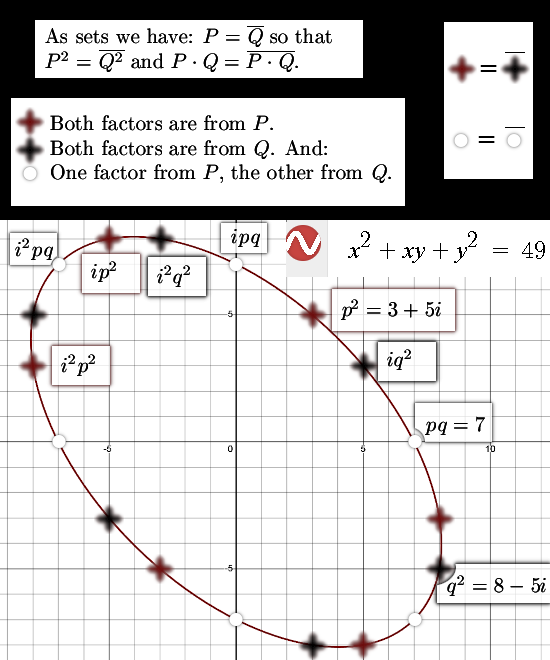
Here is a link to the free Wolfram webpage where you can check that indeed 1729 has 48 integer solutions because you can make 8 different factors with the prime numbers involved: https://www.wolframalpha.com/input?i=x%5E2+%2B+xy+%2B+y%5E2+%3D+172

Here’s the wiki: https://en.wikipedia.org/wiki/Unique_factorization_domain.
That was it for this post, thanks for your attention.