Some time after I started writing this post I thought “Hey why not look up what is more or less offically said on this theorem in the internet”. So I did and found out there are three versions of this theorem that basically says you can do integration with a primitive. That was a tiny surprise to me because the way I remembered it was there is just only one. There are two versions on the real line and one for the complex plane. The first real line version says that the integral of a function on the real line equals the difference that the primitive has in the begin and endpoint of integration.
The second real line version uses a variable in the endpoint of integration, say x, and define a primitive F(x) of a function f(x) as such. After that it must be shown that the derivative F'(x) = f(x). And the third version says you can do line integration (or integration along a curve traditionally named gamma) also using a primitive but now you must take into account the way differentiation works in the complex plane.

So there is not one such fundamental theorem but the official theory says it’s three. Now why three? Very simple: The professional math people know of no other spaces where you can do integration with a primitive. I’ve said it before and repeat it once more: The 4D quaternions are nice things but when it comes to differentiation and integration it is hard to get a bigger mess of total gibberish. That’s why the professional math professors don’t have such a fundamental theorem for the quaternions.

But for the 3D complex numbers that are the main topic of this website, it can also be done. But hey this is now the year 2025 and this website is almost 10 years old and on top of that I found the 3D complex numbers back in the year 1990, so why only now this theorem in the year 2025?
Now over the years I have always used this kind of integration when I needed it. For example the number tau for the 3D complex numbers was calculated the first time by using integration while I developed the matrix diagonalization methods only later to deal with the problems you get in say five or seven dimensional complex numbers.
For people who don’t have it clear what the numbers tau are: They are the logarithm of an imaginary unit. For example the log of the imaginary unit i on the complex plane is i times pi/2 as was already found by the good old Euler. Now for the 3D complex numbers it’s a bit more difficult but you can find such log’s of imaginary numbers indeed with integrating just the inverse.

But I always thought there would be some kind of trouble if you integrate just inside the subspaces of non-invertible numbers. So that’s more or less why I never ever formulated such a fundamental theorem in all those years. I only used integration when I needed it and that was it.

To my excuse there are indeed some subtilities, I once tried to find the primitive of say e^X and yes, no problemo, it is just e^X. While if you calculate the integral now with a 3D number X but multiply it by that famous number alpha, the primitive changes in a dramatic fashion.
So all those years I thought that even for say the exponential function there was not just one primitive to do all the work. Yet now I take a deeper look into it, this was all a bit stupid of me.
So it’s a lame excuse but compared to the professional math professors who can’t even find the complex 3D numbers, I shine as the stable genius I am… Ahum, this post is only 9 pictures long and has 3 additional figures and one video about the fundamental theorem on the real line. So all in all there are 12 pictures and 1 video below.

Lets get this party started:

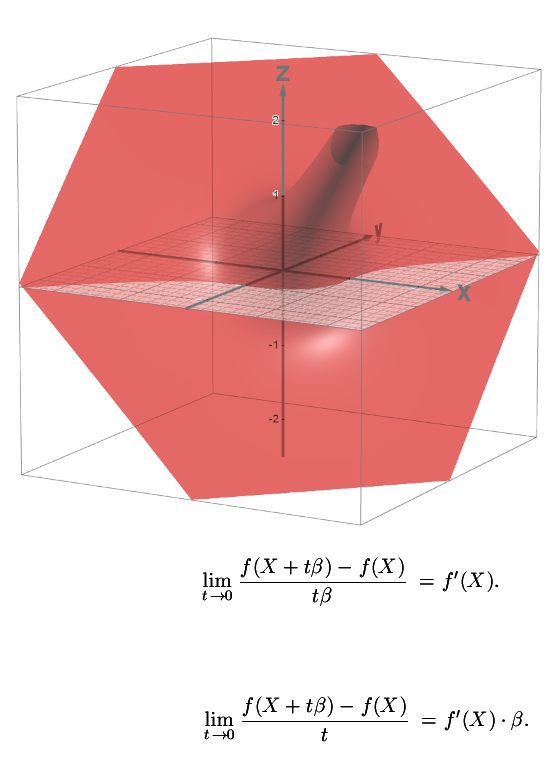
The next picture is the so called Figure 1 picture and it shows where the determinant is one. So on the red colored graph you can do the ‘divide by beta’ thing in the limit for the derivative of a function. The problems with taking such a limit on the space where det(X) = 0, you can’t divide by such a beta so doesn’t that cause some problems? Well no, you can always flip hin und her between the two above definitions of taking a derivative.

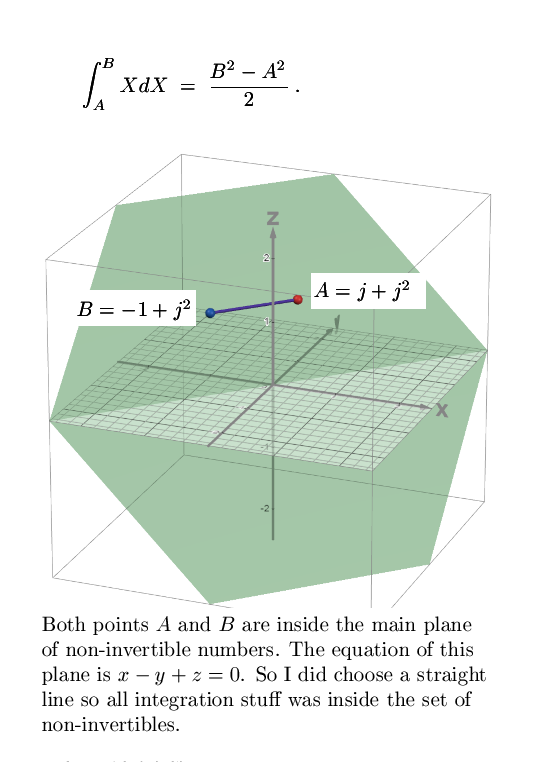
And here is the so called Figure 2 picture where I depicted a line segment inside the main plane of non-invertible numbers in the 3D complex numbers. Therefore I invite you to think a bit along those lines, does it matter if they are inside or outside the space of det(X) = 0?

I have a link for you to a page from the website from Stephen Wolfram where the three fundamental theorems of calculus are explained.
Fundamental Theorems of Calculus
Now I published the above about 24 hours ago but I was forgotten to place the link to Wolfram. And today I was watching youtube and to my surprise a video from Hannah Fry came floating along while it said it was about the fundamental theorem of calculus. It’s all very very basic because Hannah uses it also to craft an introduction to integration using the limit of an elementary Riemann sum. For most readers it is a bit too simple I guess but in case you harldy know what integration is, for those it is a very good video.

And for no reason at all I also made a cube with her face on it. We all love Hannah because she is relatively good at popularizing math. And that’s a good thing because it makes the general population a bit less stupid. Anyway that is what you might hope for but don’t let you hope become to big because the human brain and math is often not a good combination. We’re just a fucking stupid monkey species, ok we are the smartest monkeys around but we’re still a monkey species…

This is the end of this post, now we have a fourth so called Fundamental theorem of calculus. Lets leave it with that.