I wrote this post because I was curious how the world famous +/- pattern would look in case you try to do what the title of this post says. I focussed on the first two columns and there are six 2×2 minors to be found there. May be in the future I will use the result from this post in more writing around the theorem of Pythagoras for nxd matrices where the first d columns of a matrix are also a parallelepipid of dimension d. And if done properly, after making the nxd a square matrix, you can take the determinant in the way of this post and get the d-dimensional volume of the parallelepipid.

Well, we’ll see because yes you get that volume but you don’t get a proof of the matrix version of the theorem of Pythagoras for such nxd matrices.

This post is as simple as possible so if you understand the 4D case I expect you to also grasp how to generalize this to arbitrary dimension. The post is five picutes long and it is handy to have the permutation variant of calculating a determinant in the back of your head. In case you never did see that before, shame on you but you can’t help it if you are some victim of the American educational system… Here’s a link:
https://en.wikipedia.org/wiki/Determinant.

Ok here are the five picture for this post:

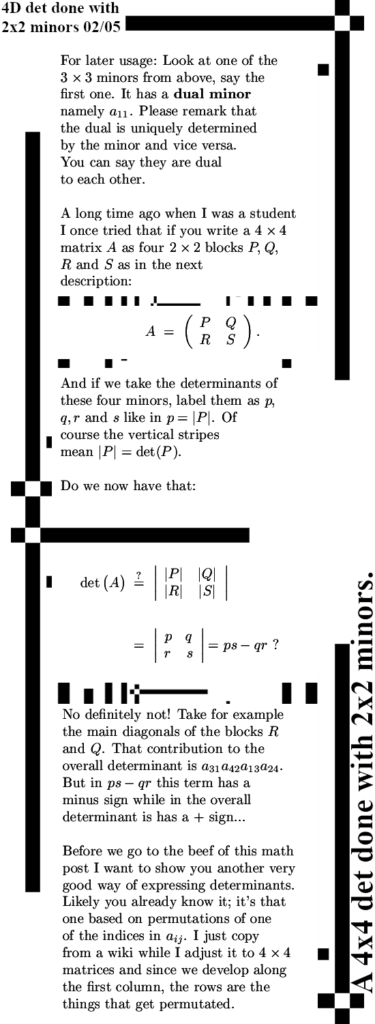
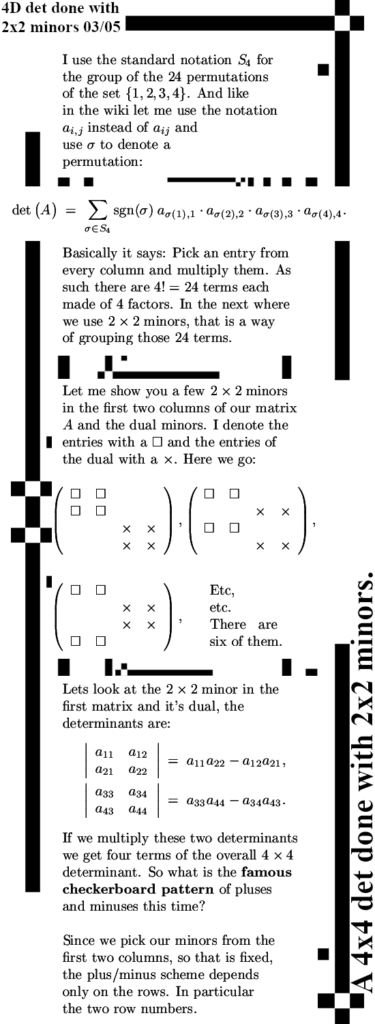
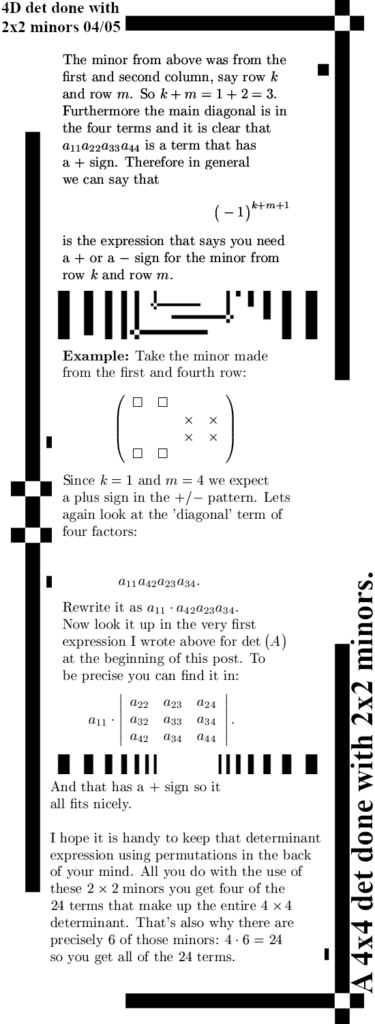
As you see: grouping this as six minor determinants multiplied against the determinant of their duals is a handy way to get all those 24 terms of each four factors a 4×4 determinant has. That was it for this math post, likely the next post is one more on magnetism and all those experiments around the so called Bell theorem. We’ll see but anyway thanks for your attention and may be see you in another post.