Some time back I was looking at a few recently published posts and I started scribbling a few calculations. And all of a sudden I realized something has gone wrong. Now that full normal vector does what it was supposed to do: Always return a normal vector even if there is only one minor matrix that is not singular. But sometimes you get a zero vector and that is not what you want of course. You can always work around it if it happens to you, so it is not a serous fault or so. But it’s all a tiny bit less perfect as I thought.

That full normal vector is something you can use if you want to make a non square matrix into a square one. In doing so you must craft new columns perpendicular to all previous columns and normalize them. And there is the problem of course: If you get a zero vector, you cannot normalize it to length one.

The reason I decided to write this post is that during my scribbling I soon got one of those cylinder equations that don’t look at all like the equation of a cylinder. But in the 3D numbers, both complex and circular, you can factorize the determinant with a plane and a cylinder equation. So in that sense it is very vaguely related to the 3D numbers.
For 3D numbers you can factorize the determinant using it’s eigenvalues and stuff like that I always name “Eigenvalue functions” because you just plug in the coordinates of a number and voila: There are your eigenvalues. It’s much easier compared to every time by hand calculating the 3 eigenvalues every 3D number has.

This post is four images long and an extra graph in a so called “Figure 01“. With the 3D version of Desmos, a free browser based app for drawing graphs, you can try a bit for yourself. I used two versions of the cylinder equation, don’t get confused by that because the one is only the minus of the other. That’s why in Desmos you sometimes must equal the cylinder equation to a positive number or a negative number. Here we go:

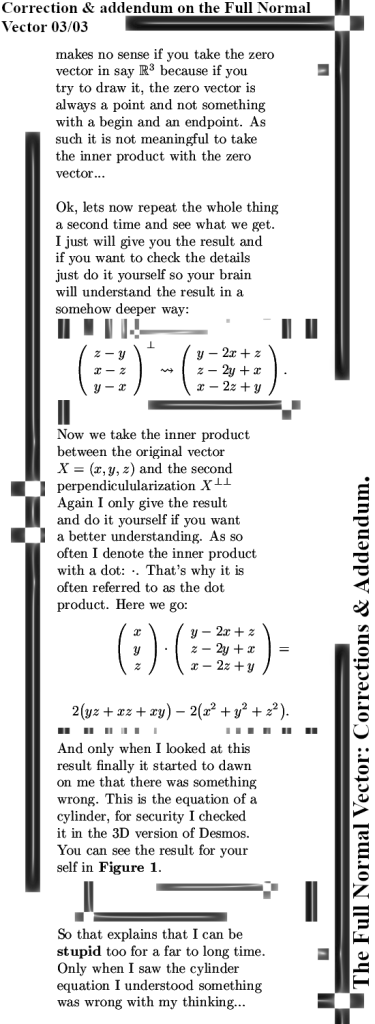
Again: If you try it in Desmos you must either use positive or negative numbers for your cylinder equation.

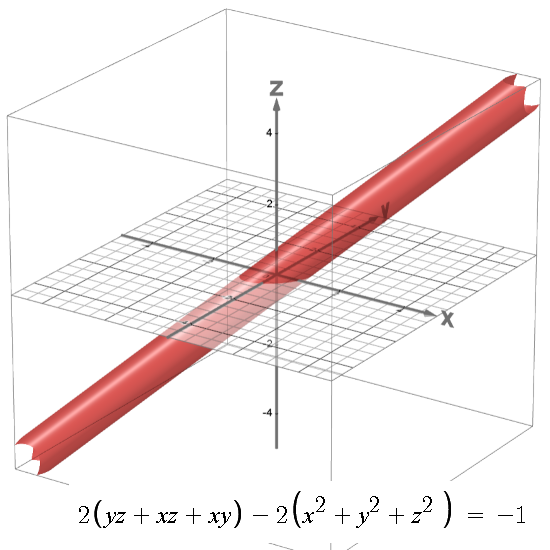
In case you want to know a bit more about the eigenvalue functions, just use the search function of this website and you will find plenty of stuff to think about. Ok, I hope you learned something and if not lets hope you are not one hundred % bored because math is just a boring thing or not?
The next post is likely about magnetism but it is also tempting to write one more post on all the possible factorizations you can do with the determinant of 3D numbers and the many ways there are to find the 3D complex exponential as the intersection of a whole lot of geometrical objects.
We’ll see.