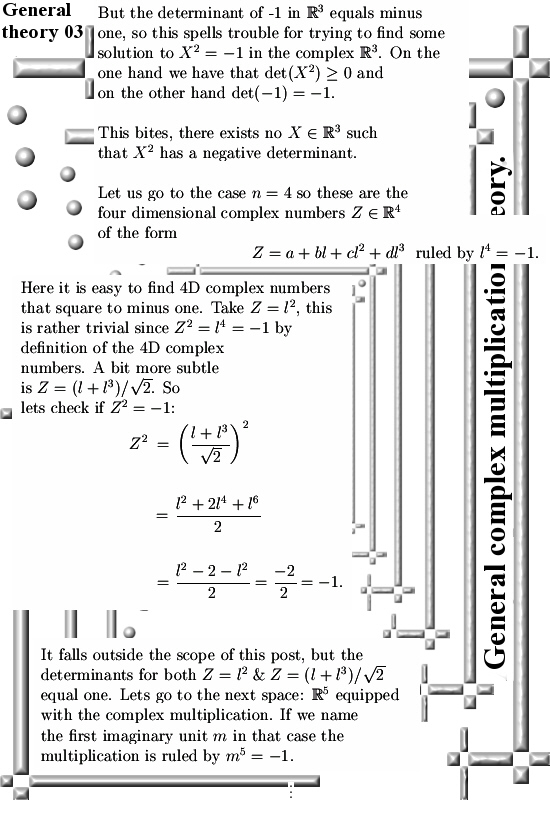
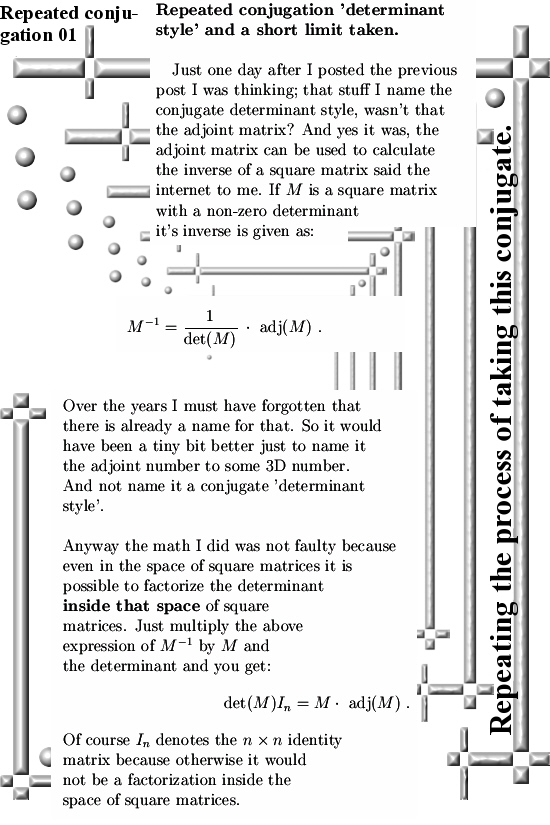
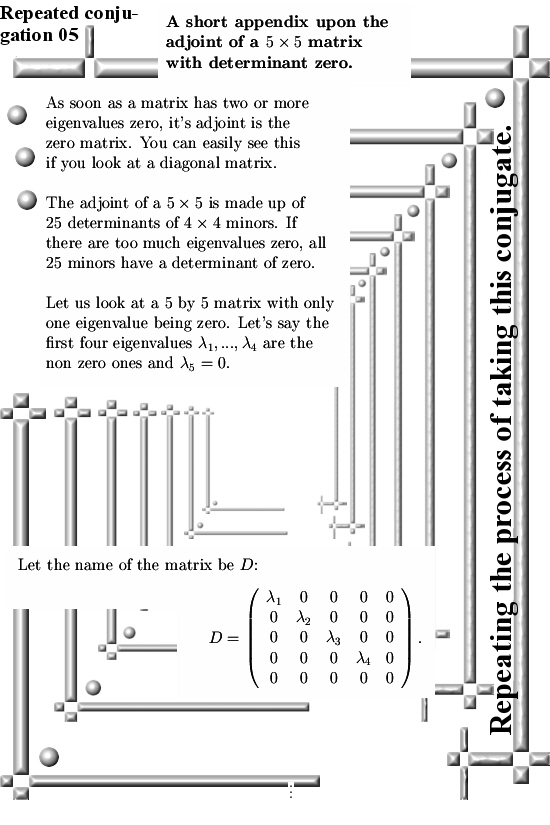
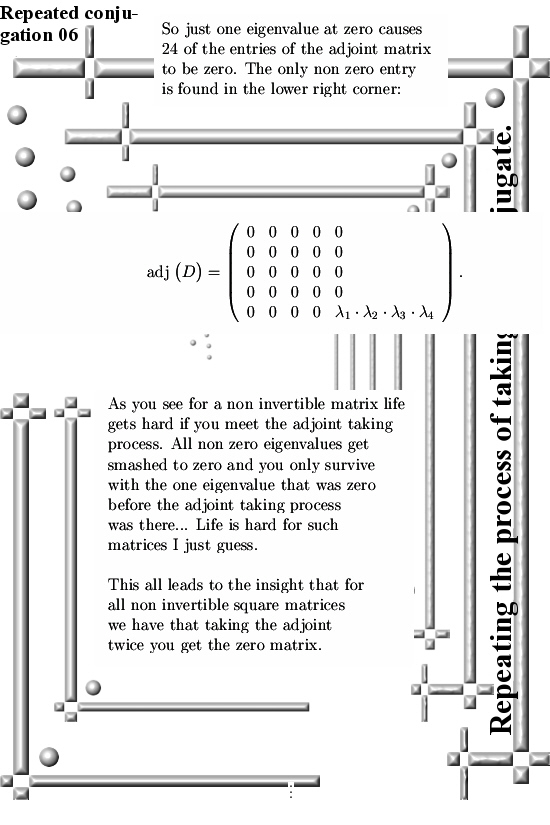
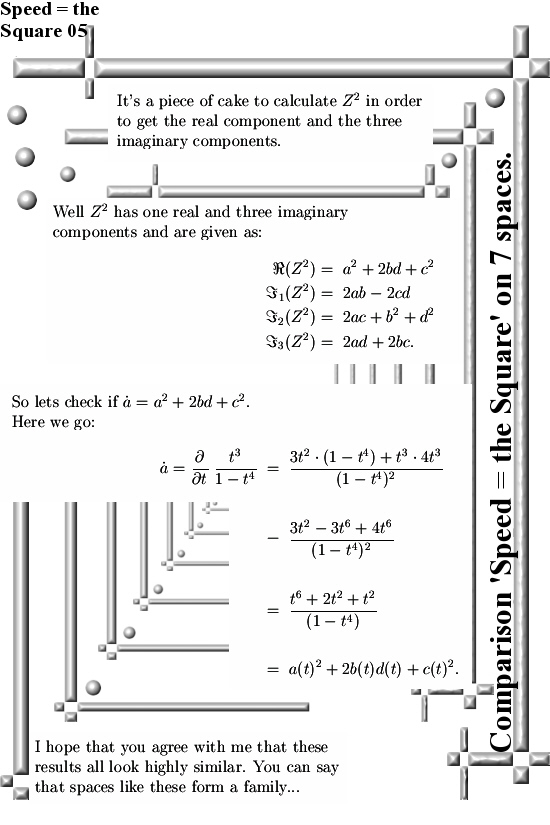
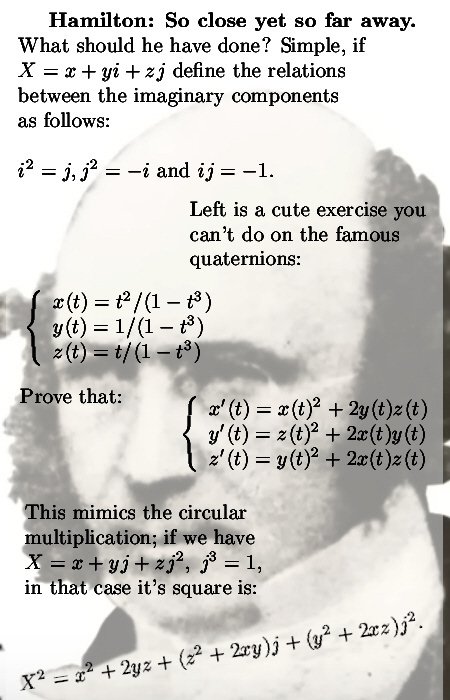There are many ways to introduce CR-equations for higher dimensional complex and circular numbers. For example you could remark that if you have a function, say f(X), defined on a higher dimensional number space, it’s Jacobian matrix should nicely follow the matrix representation of that particular higher dimensional number space.
I didn’t do that, I tried to formulate in what I name CR-equations chain rule style. A long time ago and I did not remember what text it was but it was an old text from Riemann and it occured he wrote the equations also chain rule style. That was very refreshing to me and it showed also that I am still not 100% crazy…;)
Even if you know nothing or almost nothing about say 3D complex numbers and you only have a bit of math knowledge about the complex plane, the way Riemann wrote it is very easy to understand. Say you have a function f(z) defined on the complex plane and as usual we write z = x + iy for the complex number, likely you know that the derivative f'(z) is found by a partial differentiation to the real variable x. But what happens if you take the partial differential to the variable y?
That is how Rieman formulated it in that old text: you get f'(z) times i. And that is of course just a simple application of the chain rule that you know from the real line. And that is also the way I mostly wrote it because if you express it only in the diverse partial differentials, that is a lot of work in my Latex math typing environment and for you as a reader it is hard to read and understand what is going on. In the case of 3D complex or circular numbers you already have 9 partial differentials that fall apart into three groups of three differentials each.
In this post I tried much more to hang on to how differentiation was orginally formulated, of course I don’t do it in the ways Newton and Leibniz did it with infitesimals and so on but in a good old limit.
And in order to formulate it in limits I constantly need to divide by vectors from higher dimensional real spaces like 3D, 4D or now in the general case n-dimensional numbers. That should serve as an antidote to what a lot of math professors think: You cannot divide by a vector.
Well may be they can’t but I can and I am very satisfied with it. Apperently for the math professors it is too difficult to define multiplications on higher dimensional spaces that do the trick. (Don’t try to do that with say Clifford algebra’s, they are indeed higher dimensional but as always professional math professors turn the stuff into crap and indeed on Clifford algebra’s you can’t divide most of the time.)
May be I should have given more examples or work them out a bit more but the text was already rather long. It is six pictures and picture size is 550×1100 so that is relatively long but I used a somehow larger font so it should read a bit faster.
Of course the most important feature of the CR-equations is that in case a function defined on a higher dimensional space obeys them, you can differentiate just like you do on the real line. Just like we say that on the complex plane the derivative of f(z) = z^2 is given by f'(z) = 2z. Basically all functions that are analytic on the real line can be expanded into arbitrary dimension, for example the sine and cosine funtions live in every dimension. Not that math professors have only an infitesimal amount of interest into stuff like that, but I like it.
Here are the six pictures that compose this post, I hope it is comprihensible enough and more or less typo free:





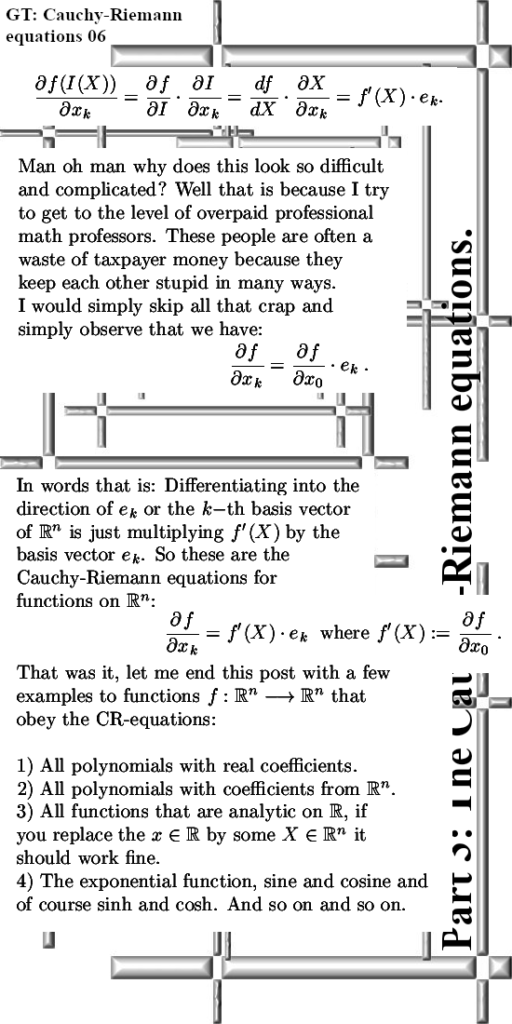
Ok that was it, thanks for your attention and I hope that in some point in your future life you have some value to this kind of math.