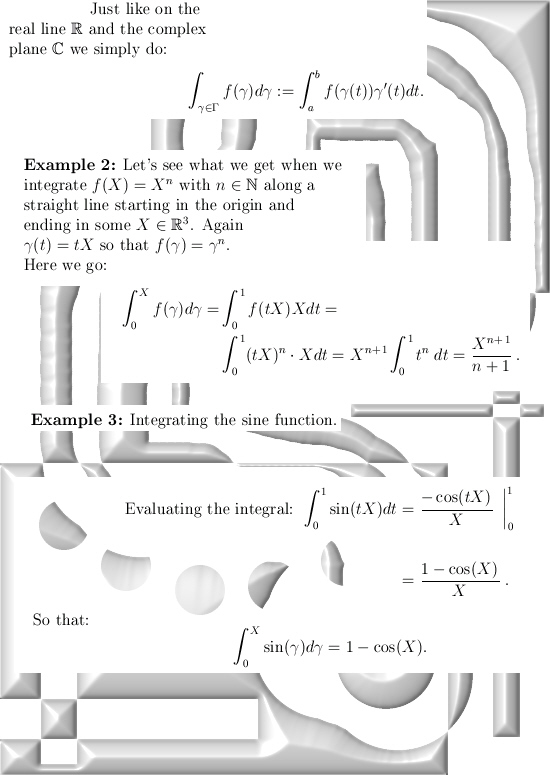
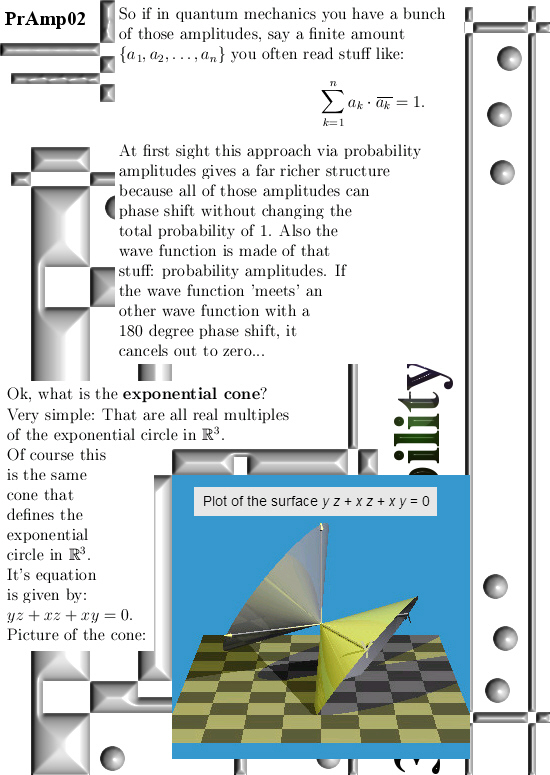
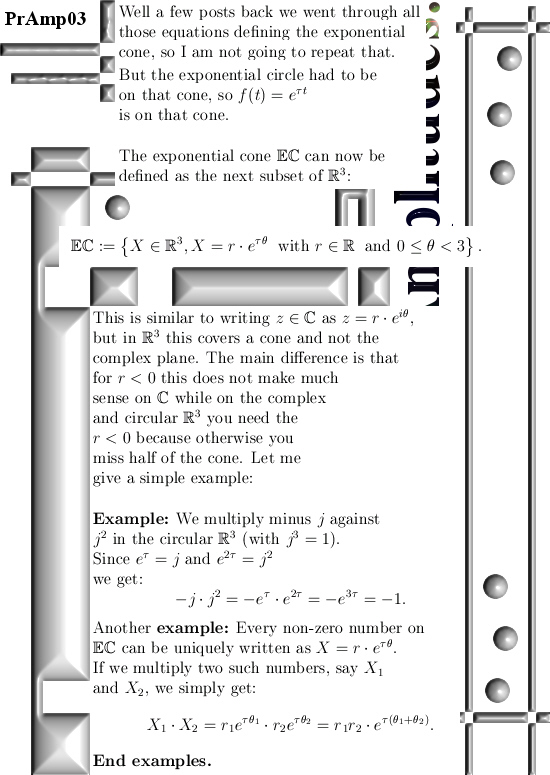
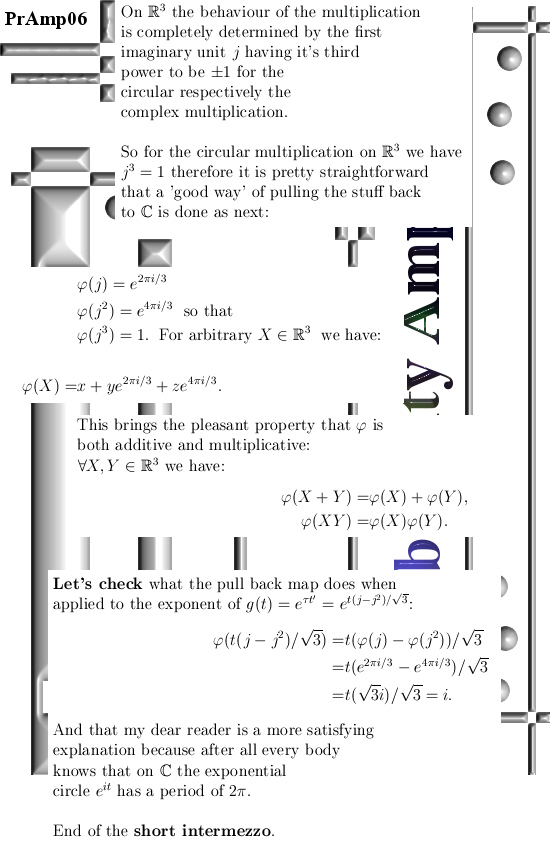
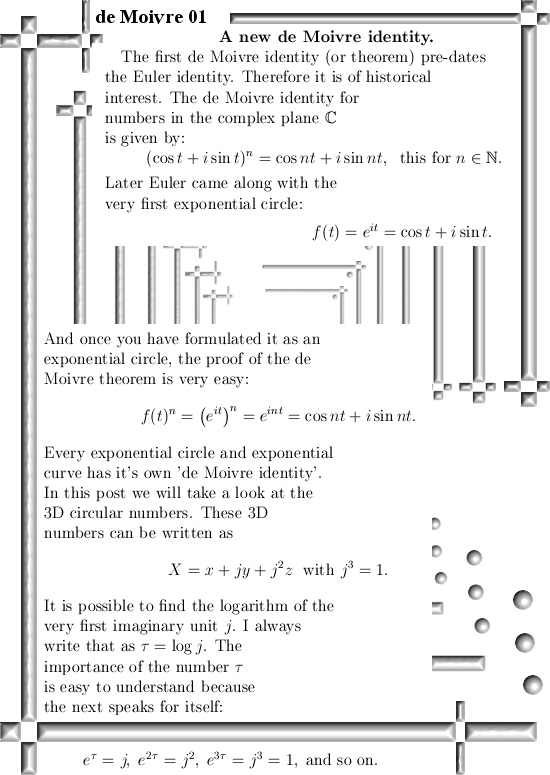
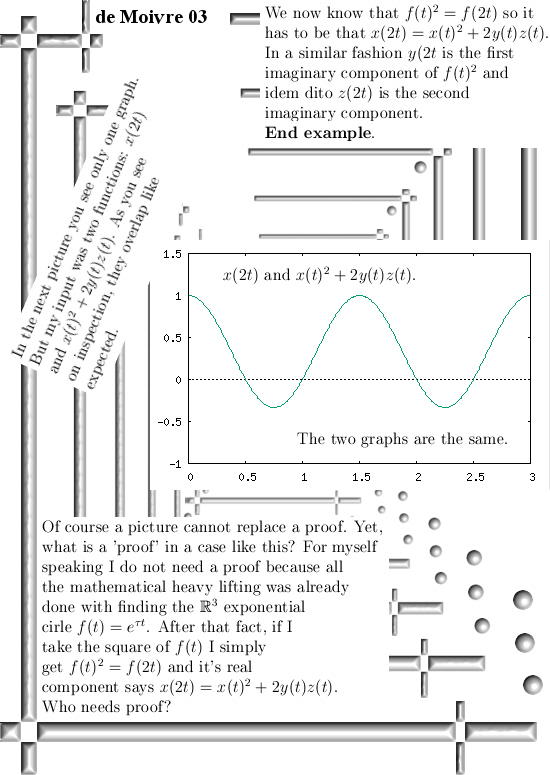
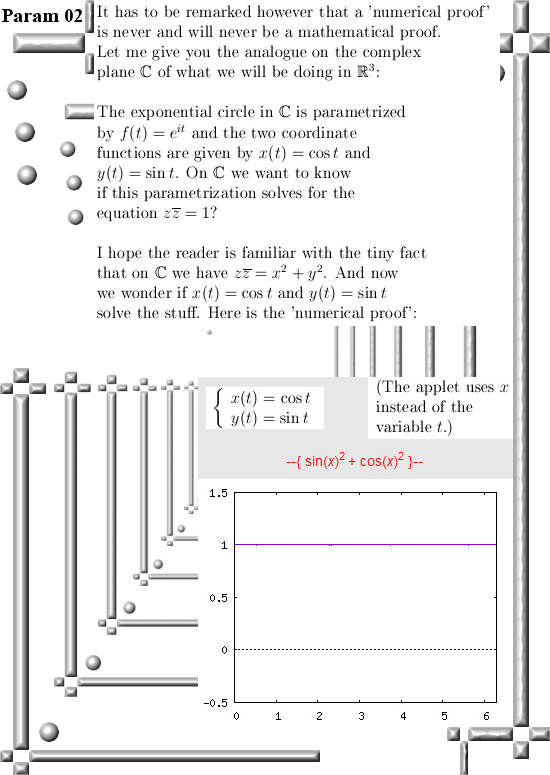
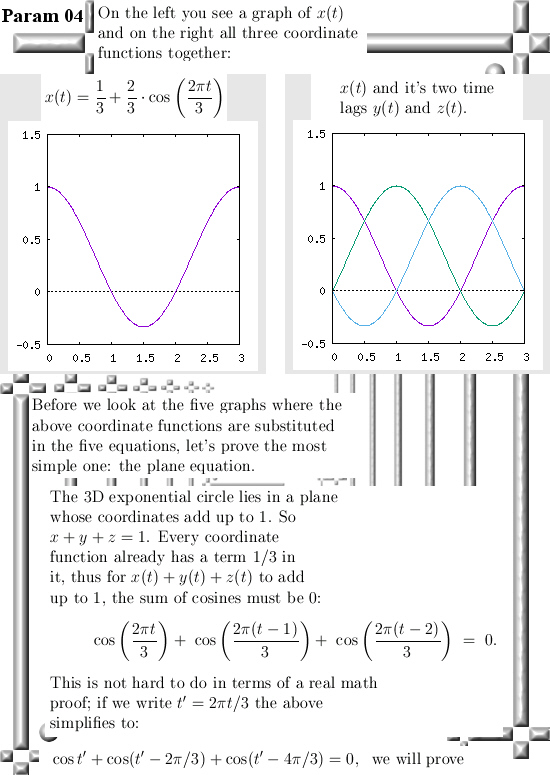
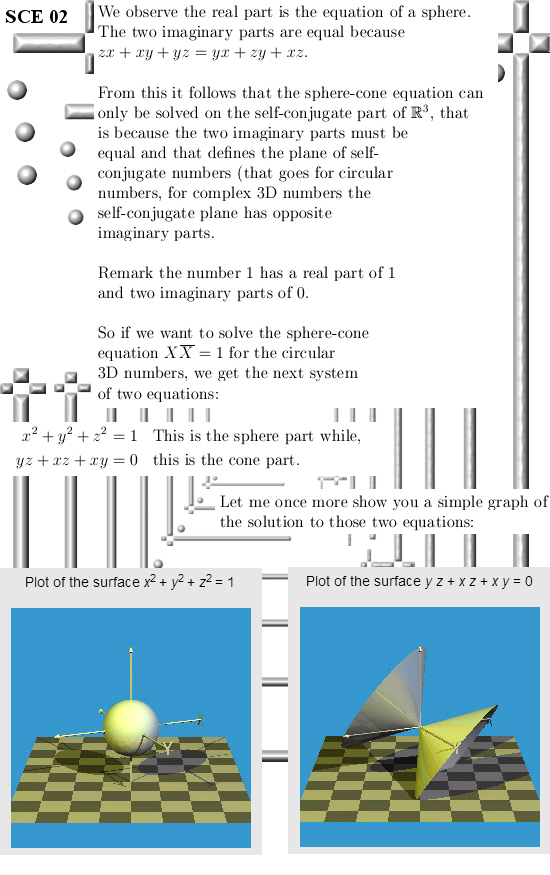
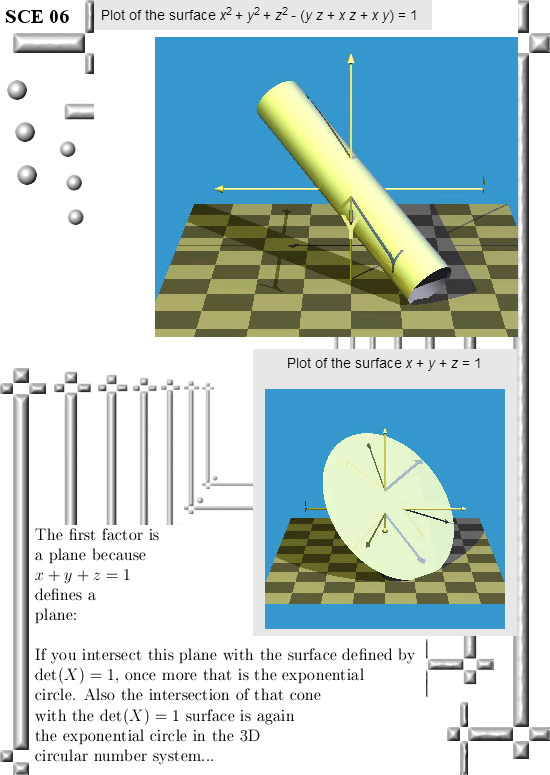
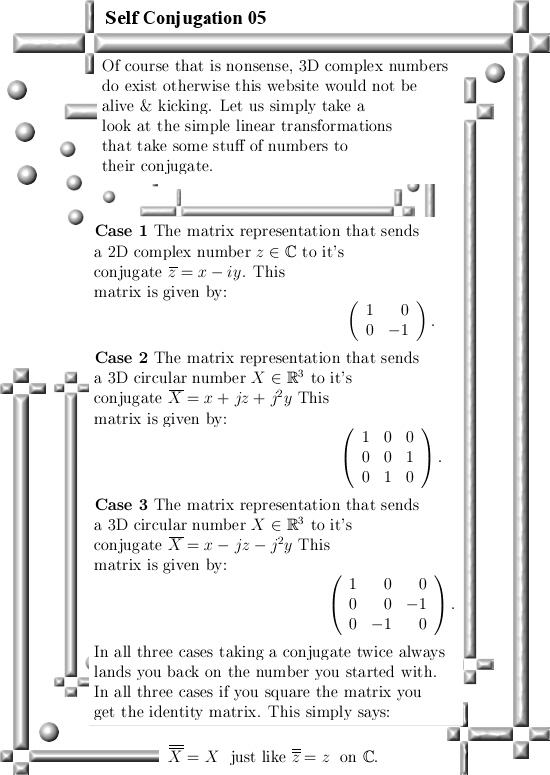
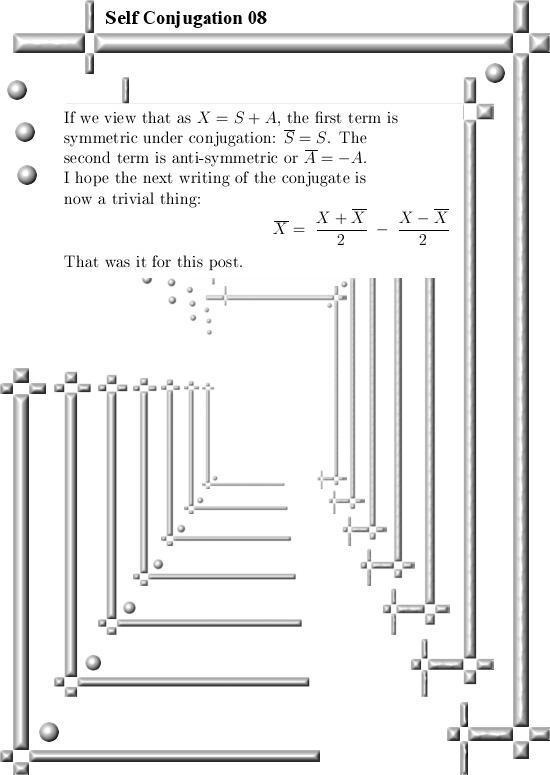
Oh oh, this is one of those posts where I only calculate in the 3D circular numbers while I classify it as 3D complex numbers. In the past when I made those categories on this website I did not want to have too many categories so that is why I only have 3D complex numbers as a category.
All in all this post (number 146 already) is not extremely important because over the years I have given many proofs that the parametrization for the exponential circle indeed fulfills all those equations like the sphere-cone equation of the fact the determinant is always one. On the other hand, if you have an important mathematical object like the exponential circles, it is always good to have as many proofs as possible. Just like there are many proofs for the theorem of Pythagoras, it would be strange if we only had one proof and nobody cares about more proofs to that theorem that more or less the central to a giant mountain of math.
What do I mean with ‘first principles’? Very simple: that is the summation formula for the exponent of a linear operator or the matrix exponential if you want. In this post I use a somehow slightly different number tau; I use a number tau that gives a period of 2 pi for the exponential circle. The reason is simple: that makes the long calculation much more readable.
Another thing I want to mention is that the long calculation is nine lines long. For myself when I read the works of other people I do not like it if calculations go on and on and on. I always try to avoid too long calculations or I just don’t write posts about them. Almost nobody reads the stuff it it’s too long and gets too complicated so most of the time I simply skip that. Beside that there is always 0% feedback from the mathematical community, so although I always year in year out try to keep it so simple that even math professors can understand it, nothing happens. Just nothing, so after all those years it is not much of a miracle I don’t want to engage with these overpaid weirdo’s at all. Likely if you are born stupid you will die stupid & I have nothing to do with that. Mathematics is not a science that is capable of cleaning itself up, the weirdo’s keep on hanging to their fantastic quaternions and their retarded ideas of what numbers & complex numbers are. Too much money and too much academic titles have not lead to a situation where the science of math is capable of cleaning itself when needed.
Enough of the blah blah blah, after all the physics professors have the same with their electron spin: where is your experimental proof that the electron is a magnetic dipole? For over five years nothing happens except a lot of weird stuff like quantum computers based on electron spin…
This post is five pictures long, for me it was cute to see how those three cosine functions slowly rise from the start of the long calculation. Also of importance is to notice that I had to use the simple formula for cos(a + b) = cos(a)cos(b) – sin(a)sin(b) that comes from the exponential circle in the complex plane. Just once more showing that 3D complex & circular numbers are indeed emerging from the 2D complex plane. Not that the math professional will react, but anyway…
Let’s go to the five pictures:


fact that the circular multiplication uses j to the third power is 1.



Again, this is not a ´very important´ post. Given all those results and proofs from the past it is logical such a long calculation has to exist. It´s relevance lies in the fact you simply cannot have enough proofs for the calculation of parametrizations of the 3D exponential circle.
Let me leave it with that. See you in the next post.