Category Archives: 3D complex numbers

The new 3D coordinate system; [a, r, t] coordinates.

May 24, 20163D complex numbers, Exponential circle, Matrix representation, Quantum mechanicsReinkoVenema

About a full week late all is now finished. Also there was that problem of the hacked webpage; the third update on the Schrödinger equation was loaded and loaded with all kinds of weird comments. But if you did read those comments you could see the overwhelming majority was not written by humans but were posted by bots.

Anyway in the end even advertisements for online sales of viagra and stuff surfaced so I took an evening to see if this could be repaired. For the time being it is not possible to post comments although before it was also impossible but that was due to an unknown technical fault…

__________

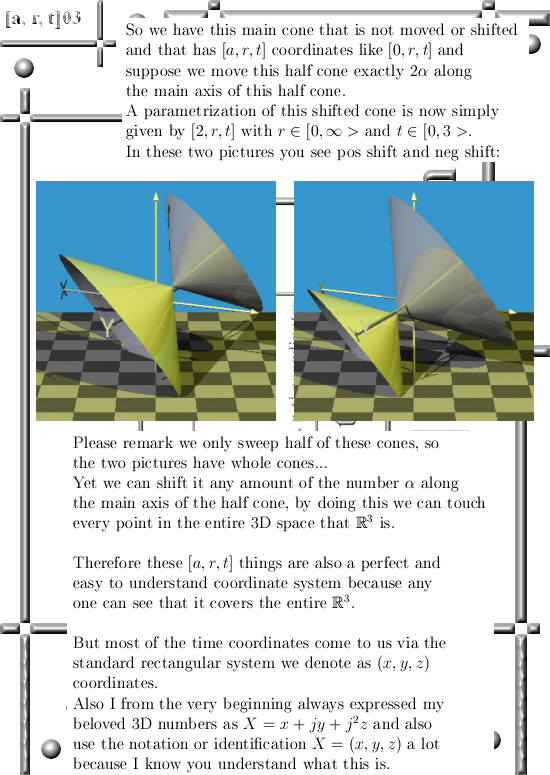
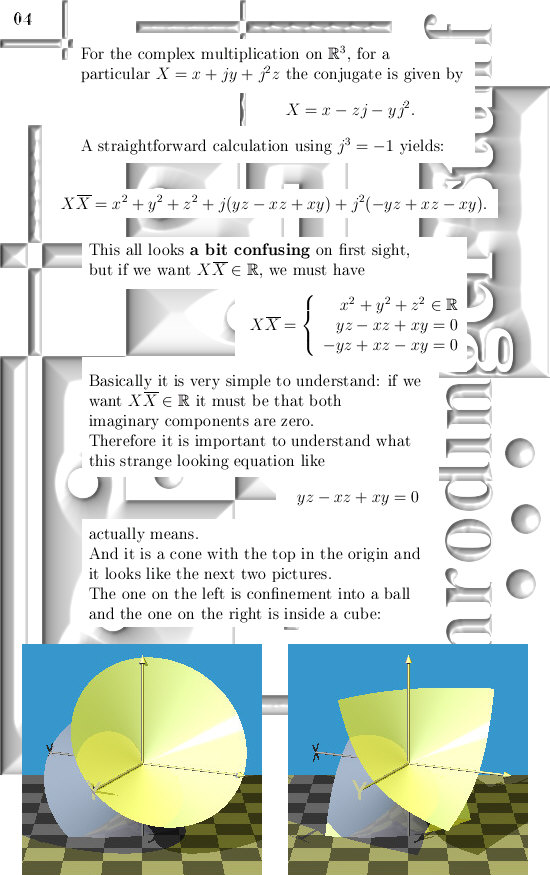
In this update we dive into the [a, r, t] coordinate system and this is very similar to using polar coordinates in the complex plane only in 3D we are moving a half-cone along a line and as such sweep through the entire 3D space. In short it goes like this:

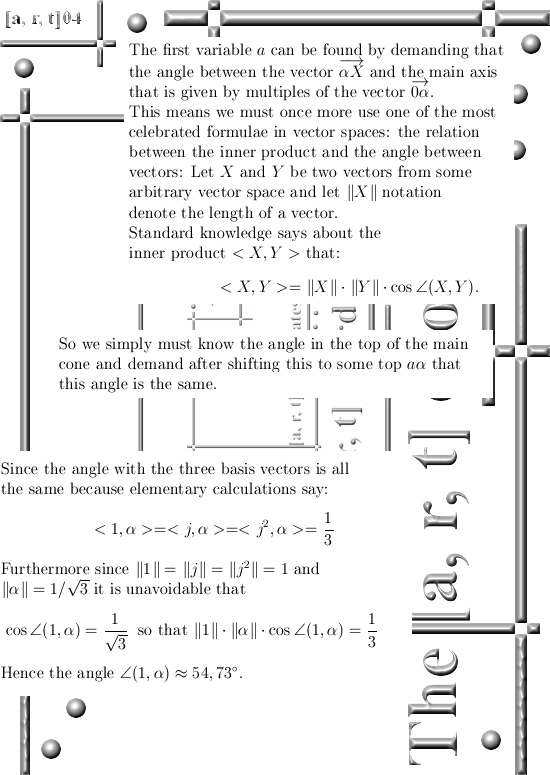
With a we control how far the cone is moved from the origin,
with r we denote the distance from a particular point X to the top of the cone and finally,
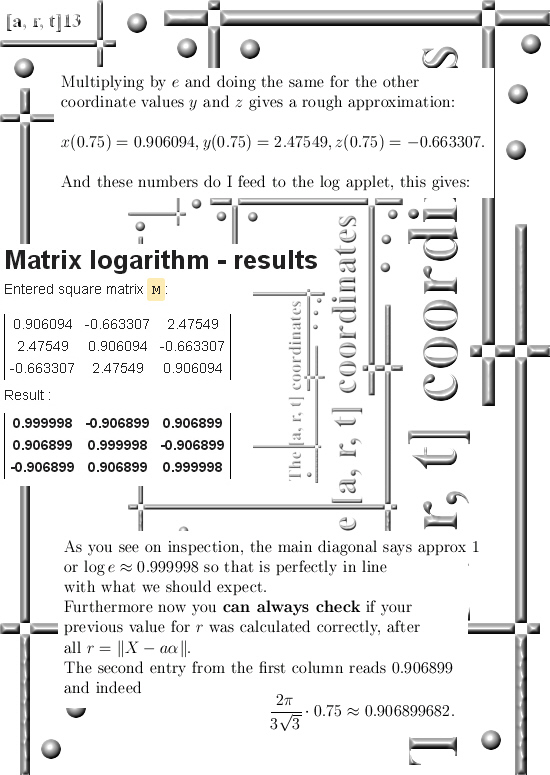
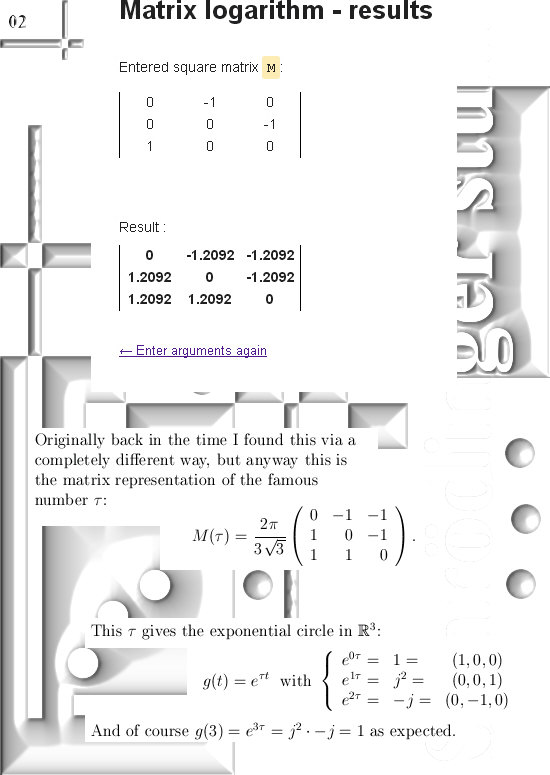
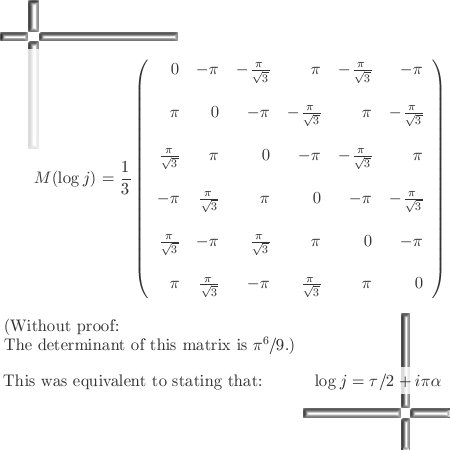
with t we figure out how much we need to rotate stuff using an applet for the log of a matrix.

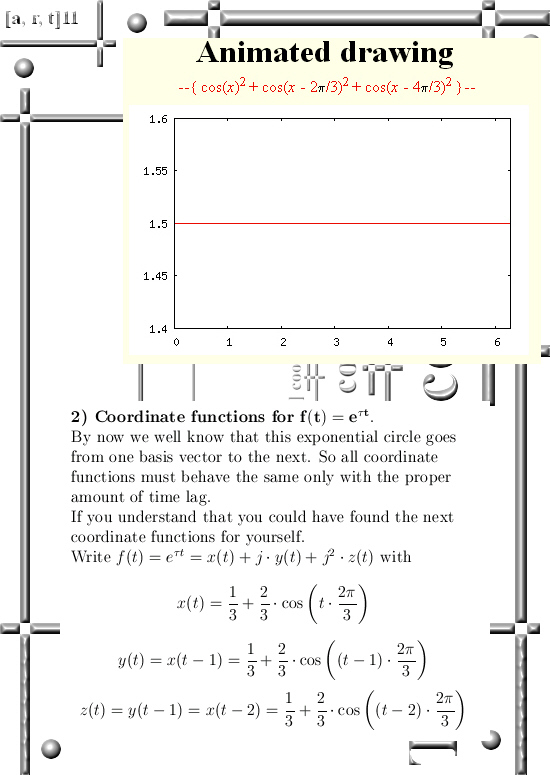
I also give once more the coordinate functions of the exponential circle so that you are able to find coordinates on the main cone (that has the origin as it’s top) for yourself.

Without prove I also give a new de Moivre formula, the original de Moivre formula is from about 50 years before Euler so after 3 centuries there is a bit of moving forward on that detail.

I also give a rather strange looking sum of squares of cosine functions that add up to 1.5; the three cosine functions all differ by 120 degrees or 2pi/3 if you want.

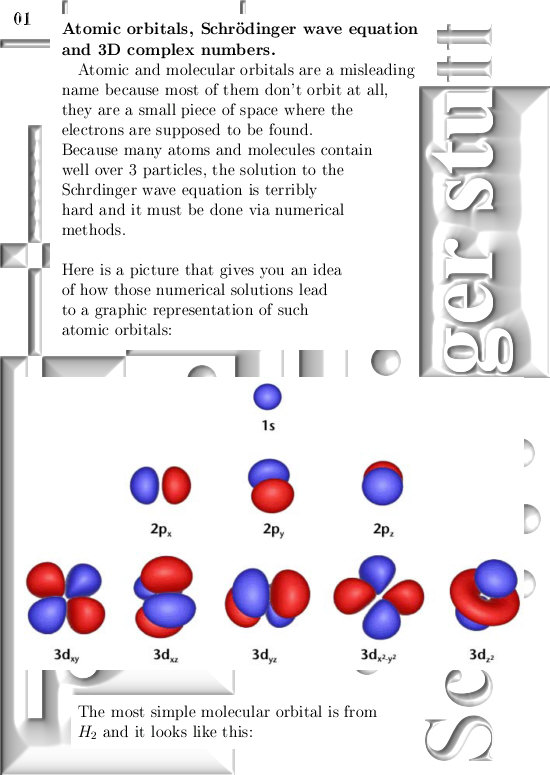
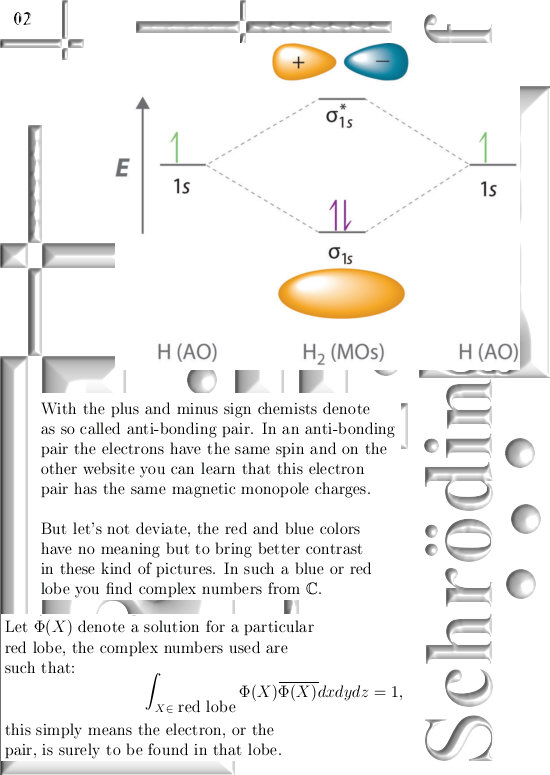
It is important to remark I did my best to keep it as simple as possible so I also concentrate on a few worked examples so it is not just theory but also how to find these new coordinates. In relation to other posts like the Schrödinger equations posts, I think this new coordinate system is definitely of interest to people from quantum physics and chemistry that try to calculate those atomic and molecular orbitals.

This update is relatively long: 14 pictures of size 550 x 775 pixels and for the first time I use unshrunk jpg pictures because year in year out the bandwidth of internet connections is still rising fast so why remove fine detail from jpg pictures any longer?

__________

I hope you learn something new, here are the pics:

Ok, that was it. For myself speaking I more or less expect everything to be the same:
Professional math professors from around the globe will keep on talking about their own research and just how important it is to use complex numbers from the complex plane.

A few useful links:

De Moivre’s formula
https://en.wikipedia.org/wiki/De_Moivre’s_formula

And a good applet for the logarithm of matrix representations is also handy:

http://calculator.vhex.net/function-index/linear-algebra
http://calculator.vhex.net/function-index/linear-algebra

And last but not least is a proof for the latest formula above: the circular multiplication on the [a, r, t] coordinates can be found on the other website:

From 06 May 2016 : On the length of the product of two 3D numbers.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff04.htm#06May2016

Let’s leave it with that. Till updates.

Things have grown emotional and chaotic. But there is a glimmer of hope…

May 15, 20163D complex numbers, Exponential circleReinkoVenema

Oh oh all of a sudden all kinds of things that are highly emotional and non-mathematical arise. Stuff like a close but young family member still being suicidal and a young neighbor that was arrested by the local police and is now in the intensive care of the local psychic hospital.

And to finish it off, all of a sudden after waiting far too many years I decided to press some child neglectance/abuse charges related to the boy in the intensive care.
And, just a detail: If you have a very severe spychotic behavior like the boy in the IC of course this could have a pure biological foundation.
But if your mommy is a full blown psychopath this does not do much good either…

Yet I have to say that although this stuff is highly emotional I think I like it.
After all these years finally there could be a small chance of fundamental change for those kids suffering from the psychopath mommy…

We will wait and see.

__________

On the math front I have not been sitting on my hands but stuff is not finished by far.
So the new coordinate system has about one week of delay.
On the naming of the coordinate system it is just about thinking about the name for a new baby and I am more and more leaning to the name that is also a functional description:

[a, r, t] coordinates.

Why not? The three letters a, r and t are how you need to calculate them in that very order.
And the word art stands for stuff that is supposed to be beautiful but also make you think a bit more. As the days go by the less I am in favor of naming this new coordinate system with names like:

Cone coordinate system, or
Conial coordinates, or
Shifted cone coordinate system, or
More stupid names.

No, why not choose [a, r, t] coordinates as the name for this new coordinate system?

On the other website I have posted the first update that studies how the length of two 3D circular numbers change when you multiply them. So given the reactangular coordinates (a, b, c) of A and (x, y, z) of X, what is the length of the product AX?

Here is the link:

From 06 May 2016 : On the length of the product of two 3D numbers.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff04.htm#06May2016

Ok let me end this update, till the next post.

A brand new coordinate system for 3D complex and circular numbers under development.

May 3, 20163D complex numbers, Exponential circleReinkoVenema

With great success I was able to kill my frustration. There are many ways to combat heavy upcomming frustration, for example you could go running against the wind until you are so heavily exhausted that all frustration is gone.

But this time I did it differently: Within a timespan of at most three minutes I finally wrote down that calculation that I avoided for so long, for so many years. And within this small time frame suddenly I was bombarded by sphere and cone equations telling me that story I should have discovered so many years ago.

Within this unloading of a huge amount of frustration I discovered how the length changes when you multiply two 3D cokmplex numbers, say X and Y.
All these years I never understood properly what drove the length of the product XY.

And this result eased my mind, I was no longer frustrated that all those incompletent people get boatloads of money every month while I live in relative poverty compared to those saleries.
And I went to work and I discovered an amazingly strange but also very easy to understand completely new coordinate system for 3D space.

It is not for any ordinary 3D vector space, you must equip it with either the complex or circular multiplication, but it is so beautiful that I hope it will survive in the long run.

I have not decided on a name yet, for the time being I name it ‘special coordinates’. Since cones play such a major role the name ‘cone coordinates’ might be the right thing to do.
But there are already Conical Coordinates yet they act like the common point of 3 non parallel planes; it is the intersection of two cones with a sphere…

__________

All in all I will post the stuff on length preserving/shrinkage/extra growth on the other website in page 4 on the higher dimensional complex numbers.

And on this website I will post an entry with this new coordinate system

So that’s the planning for the time being, till updates.

Third post on the Schrödinger wave equation using 3D complex numbers for atomic & molecular orbitals.

April 13, 20163D complex numbers, Exponential circle, Exponential curves, Matrix representation, Quantum mechanicsReinkoVenema

This update is 10 pictures long, the pictures are sized 550 by 775 pixels.
This update covers more or less everything, but I still have to explain how you find the six coordinate functions the poeple will need in order to see if these kind of complex numbers give the same result as ordinary complex numbers from the complex plane.

For those that cannot wait: In the post from 03 April I posted a teaser picture with the coordinate functions in 3D, if you multiply this against the e to the power i pi alpha thing in this update you have the six coordinate functions…

Ok ok you neatly have to write them out, but basically it is all there.

At first I was thinking it would be hard to get different results using these higher dimensional complex numbers, but when talking about atomic and molecular orbitals it might be more subtle than it looks. At the end I will post a video where some physics guy shows all kinds of orbitals related to hydrogen but his stuff is different from the pictures we observe in chemistry.
He explains this by saying that the people from chemistry always take a super-position of two wave-blobs and as such it gets oriented along the y-axis say.
If you would take super-positions of my 3D complex numbers you will get very similar results. look at the drawing in the one before last picture:
Take a super-position of an exponential circle and it’s conjugate and observe it must have the same behavior as 2D numbers from the complex plane.

(In that drawing your eys is supposed to be along the line through zero and alpha, so zero is right behind the center of the shown circle…)

Enough of the bla bla bla, here are the 10 pictures:

Click on the picture to get a larger version of the drawing:

Now finding these atomic & molecular orbitals is very hard, for simple atoms like hydrogen it is doable but what about uranium or some nice protein with only 3693 atoms in it?

All that kind of stuff falls under what we name n-body problems and for n above 3 it seems impossible to find exact analytical solutions.

There is a nice video out there explaining a bit more on the topic of finding the shapes of atomic & molecular orbitals. It is from Brant Carlson and has the title Hydrogen atom wavefunctions:

Ok, that was it for today. Till updates.

Teaser picture for the third post on the Schrödinger wave equation.

April 11, 20163D complex numbers, Exponential circle, Quantum mechanicsReinkoVenema

The stuff is more or less finished, I only have to turn it into a series of pictures so tomorrow or the day after I will post the third post on the Schrödinger equation using higher dimensional complex numbers.

Now on the other website I posted a teaser picture and since we are against cruel discrimination of peace loving websites why not post it here too?

So that is our post for today: Just a teaser picture:

Yeah yeah, once more we observe mathematical perfection.

Till updates.

Some good math for the physics community.

April 3, 20163D complex numbers, Exponential circle, Exponential curves, Quantum mechanicsReinkoVenema

Ok ok I made a relatively big blunder when sending the people from quantum mechanics using the Schödinger equation into the direction of the 3D complex numbers.

Because as a matter of fact, you cannot solve the factual Schrödinger equation in the 3D complex number system because there is no famous i to be found with the property that i^2 = -1.

You need a more advanced number system and I will explain that in detail in an upcoming post number three on the Schrödinger wave equation.

__________

In the meantime, it has not fallen on deaf ears on my side that after I posted the first Schrödinger post and I later did an internet search, suddenly with the search phrase ‘3Dcomplexnumbers’ I suddenly ended on number 1, 2 and 3.
So like expected it drew a lot of attention.

Therefore I would like to give a kind of present to the physical community because also not fallen on deaf ears, as far as I observe it physics people always try to use a product integral when they can.

Product integrals were my first serious mathematical invention, I found them while I was still trying to get my first year exam al the local university. Math professors almost never use product integrals because they are to stupid for that but physics people often put it in product integral representation.

How the history of that detail is I do not know, may be Paul Dirac had a bit to do with it…

Anyway, some time ago I wrote a pdf with the title

A tribute to Euler. Title: Ten styles for product integrals and product differentiation.
http://kinkytshirts.nl/pdfs/Product_integrals.pdf

__________

So far for the gift or the present, if you want to use other number systems beside the complex plane for depicting atomic orbitals or whatever you want to do with it, you also must know more about exponential circles and curves.

Physics people use so called ‘phase shift’ all of the time, but that is only multiplying some stuff with e to the power it or so. This is the sandpit exponential curve for toddlers.

In the world of the grown ups we have all kinds of other exponential circles and curves and guess what? I have a pdf for you with another 10 pieces of exponential circles & curves:

An overview of exponential circles and curves.
http://kinkytshirts.nl/pdfs/10_exponential_circles_and_curves.pdf

A possible way of parametrization of 3D exponential circles is given in the next picture and understanding this stuff is important when it comes to the third post related to the Schrödinger equation:

This is the end of this intro to the third Schrödinger post.
Have a nice life or try to get one.

Till updates.

Schrödinger wave equation part 2.

April 1, 20163D complex numbers, Laplacian, Quantum mechanicsReinkoVenema

A few posts back I wrote a bit about the Schrödinger wave equation related to calculating atomic and molecular orbitals for electrons using 3D complex numbers.

What I said was basically correct but also an over-simplification of the situation.
The problem is very very basic: in the 3D number system, let it be complex or circular, you just cannot solve and equation like $X^2 = -1$.
Hence the number i from the complex plane with i^2 = -1 just does not live in 3D real space.

So using alternative number systems outside the complex plane is not a straightforward thing to do, yet in principle all higher dimensional complex numbers should give the same results.
If not there would be a very basic problem inside the wave equation from quantum mechanics and I am not aware of any faults in that detail of the quantum theory.

Here are two pictures that serve as an addendum on the previous post on the Schrödinger equation:

Now if you are reading this it is very likely that at least once in your life you have seen a solution to the Schrödinger wave equation like the ‘particle in a box’. And that is not a 3D box but the one dimensional box or just an interval of the real line.

Solving the Schródinger stuff for atomic and molecular orbitals is a very different kind of game; these are always many particle systems where every particle influences the system and the entire system influence the individual particles.
Mathematically speaking it is a nightmare; analytical solutions are not possible they say.
It can only be solved numerically…

__________

But keep on dreaming, after all they also say decade in decade out that electrons are magnetic dipoles. There is no experimental proof for that only theoretical bla bla bla.

Let’s leave it with that. Till updates.

When did I find the first exponential circle in 3D space?

March 25, 20163D complex numbers, 5D complex numbers, Exponential circleReinkoVenema

It was in the Spring of 2013 when I was walking in a nearby park when it suddenly dawned on me that this exponential process that ran through the basis vectors (1, 0, 0), (0, 1, 0) and the z-axis unit vector (0, 0, 1) was periodic.
It could not be anything else because I was capable of calculating the logarithm of the first imaginary unit j.

I remember at first I just did not have a clue it would be a circle, I even had vague fantasies like may be it is a vibrating string where all those string physics professors talk about.

Now this evening I was just Googleing around a little bit when I came across this picture again:

It dates back to 30 May 2013 and I used this picture as a joke about how professional math professors look in my fantasy world. Within a week I found that the 3D complex periodic curve was in fact a circle.
So I had to laugh hard about my own joke once more because if I had known the 3D periodic thing would also be a circle I would have made the joke very different… Because one way or the other this picture now also represented me.

__________

You know this last week I am a bit puzzled by what the next post should be, in December 2013 I conducted a good investigation into the roots of unity related to the two exponential circles and because every body knows roots of unity it would a nice started for this website.

On the other website you can find it at the 05 Jan 2014 entry:

The song of omega reloaded
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#05Jan2013

At the time I was amazed with all the things you can do with the eigen values of the imaginary components j and j squared. From diagonalization to the roots of unity, my theory got definitely air born.

Later in January 2014 I found a new Cauchy integral formula (actually two just like I found two sets of roots of unity each for the admissable forms of 3D multiplication). Also in Jan 2014 I cracked the problem of 5D complex numbers.

By all standards, as far as I can see it; the two months Dec & Jan in that time were the most productive ever.

__________

Now, almost 3 years later finally stuff on Google take off, for example if this day I start searching for the phrase 3dcomplexnumbers it returns back three results from this new website.
Just look at the next screen shot picture:

So after waiting all these years, finally I begins to look as if stuff starts getting air born on some bigger scale than before.

Ok, end of this update. As usual till updates!

Atomic orbitals, the Schrödinger wave equation and 3D complex numbers.

February 29, 20163D complex numbers, Exponential circle, Laplacian, Quantum mechanicsReinkoVenema

The numerical use of three dimensional complex numbers is almost the same as the situation on the complex plane. This is caused by the simple fact that only on the main cone that includes the three coordinate axes, we have that if you multiply a number X by it’s conjugate, the result is a real number.

In the complex plane this is valid for all numbers in the plane but in higher dimensional complex number systems the situation is different; you must always pick numbers from that main cone where also the exponential circle lives (in 3D) or exponential curves (in higher dimensions).

This update is 5 pictures long, size pics = 550 by 775.

__________

One hour later:

Shit! There is a serious problem with uploading the pictures, they get uploaded but they are not visible… So you must wait at least one day longer because I do not understand the problem at hand…

Till updates.

__________

Problem with the jgp pictures is solved; according to my webhost provider it was caused by the name Schrödinger because that contains an o with two dots: ö.
My computer can handle filenames with ö so for me they looked normal but the server that hosts this website cannot deal with these kinds of symbols…

Anyway after a few days here are the pictures:

Well I am happy this strange problem of invisible pictures has been solved. Till updates.

A new type of Cauchy integral formula.

February 28, 20163D complex numbers, Exponential circle, Exponential curves, Matrix representationReinkoVenema

Yesterday I wrote a new post on the Schrödinger equation using 3D complex numbers but before I post that let’s go a bit more hardcore with a brand new Cauchy integral formula.
Actually it is not that brand new because on 18 Jan 2014 I posted it on the other website.

Now in a normal world a brand new Cauchy integral would be greeted with a lot of joy and plenty of discussion, yet that has not happened by now. Once more we observe that among professional math professors there is a severe problem concerning the so called ‘competence question’.
Or may be it is better to frame this into a lack of competence; if you have that you are also not able to judge new results properly and this is what we observe year in year out.

But I have to admit it is a relatively hardcore update, it is 10 pages long and I remember clearly it was fun to write because I wanted to prove the Cauchy formula in this way for a long time.

Source: http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#18Jan2014

__________

Now a person that is not 100% insane might wonder how the hell you calculate the determinant of a six by six matrix because in parctice that is an awful amount of work. But I used an internet applet and as such got a numerical value like about 106,821 and within a few seconds I recognized this as being pi to the power of six divided by nine.

Once back in the year 1992 I came across that number and it was kinda weird to observe that in 2014 it was still floating around in my brain. Sometimes I wonder if I am the crazy one and the math professors are the ones with healthy brains…;)

Ok, till updates my dear reader.