Category Archives: Exponential circle

Some very rudimentary Fourier stuff + a surprising way to do a particular integral.

May 22, 20173D complex numbers, Exponential circleReinkoVenema

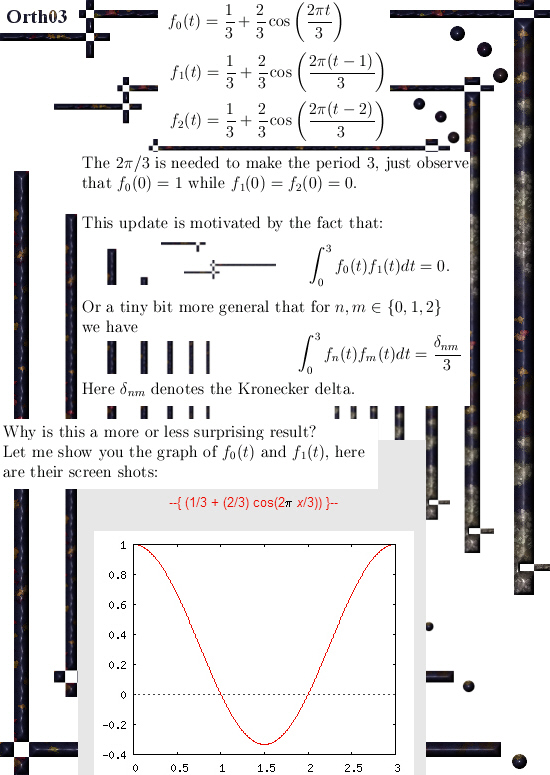
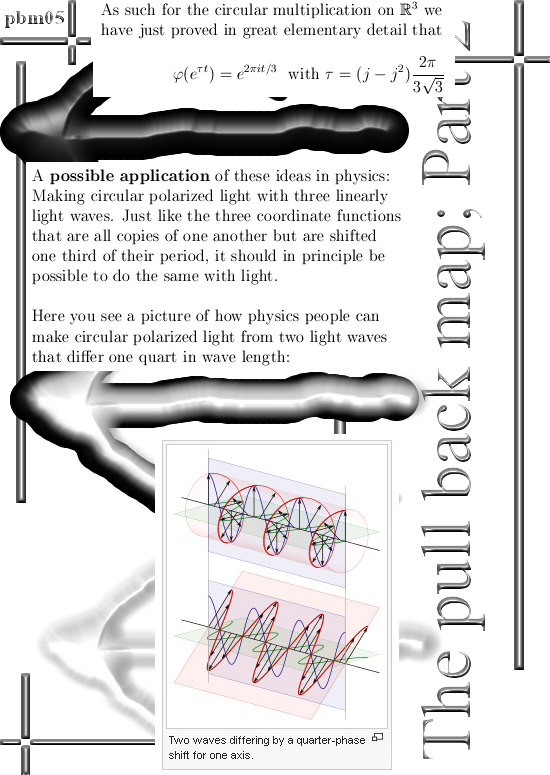
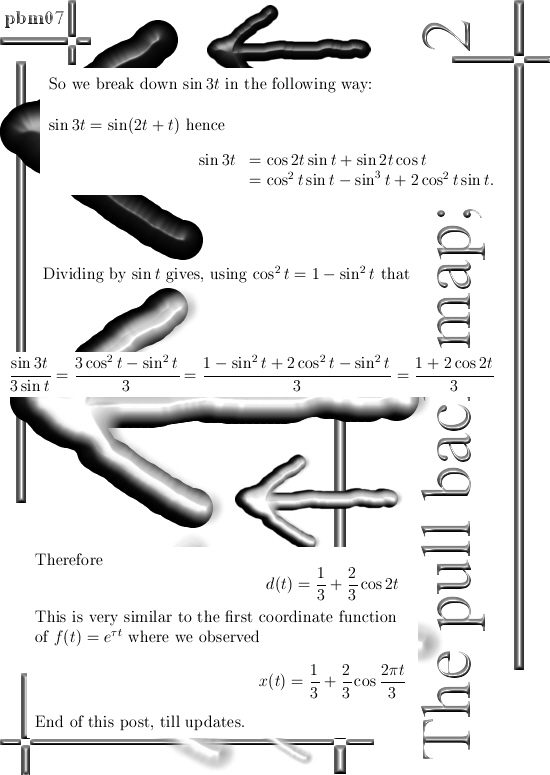
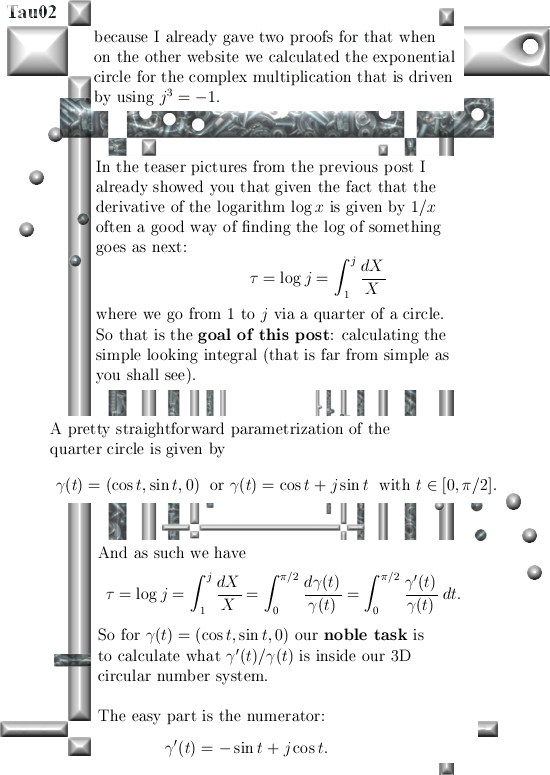
Lately I was looking at some video’s about Fourier analysis and it dawned on me I had never tried if the coordinate functions of my precious exponential circles were ‘perpendicular’ to each other.

Now any person with a healthy brain would say: Of course they are perpendicular because the coordinate functions live on perpendicular coordinate axis but that is not what I mean:
Two functions as, for example, defined on the real line can also have an inner product. Often this is denoted as <f, g> and it is the integral over some domain of the product of the two functions f and g.

That is a meaningful way of generalizing the inner product of two vectors; this generalization allows you to view functions as vectors inside some vector space equipped with an inner product.

Anyway I think that most readers who are reading post number 62 on this website are familiar with definitions of inner product spaces that allow for functions to be viewed as vectors.

__________

So I was looking at those video’s and I was highly critical if my coordinate functions would be perpendicular in the sense of such generalized inner product spaces. But indeed they are also perpendicular in this sense. Yet a bit more investigations soon gave the result you cannot build a completely new kind of Fourier analysis from this stuff.

Ok ok a few years back I already arrived at that insight because otherwise in previous posts you would have found stuff relating to that…

Generalized inner product spaces are often named Hilbert spaces, a horrible name of course because attaching a name like Hilbert to stuff you can also give the name Generalized Inner Product Space brings zero wisdom at the scene.
It is only an attempt to turn the science of math into a religion where the prophets like Mr. Hilbert are given special treatment over the followers who’s names soon will be forgotten after they die.

More on Hilbert spaces: Hilbert space
https://en.wikipedia.org/wiki/Hilbert_space

__________

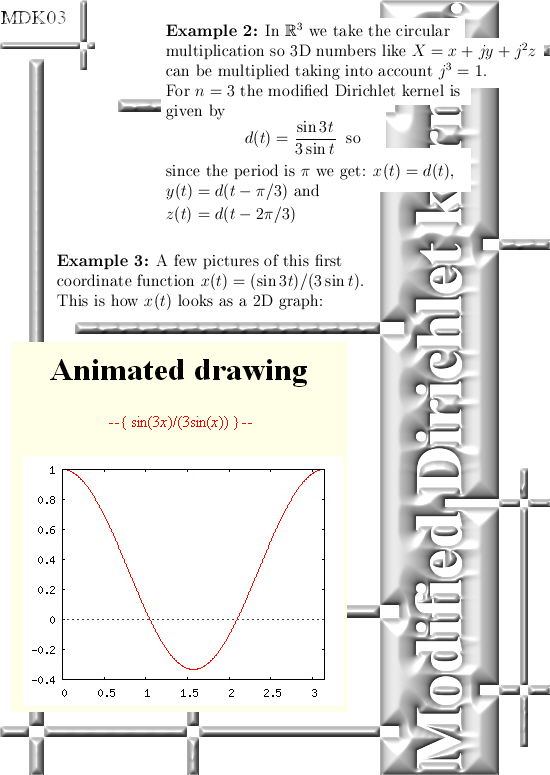
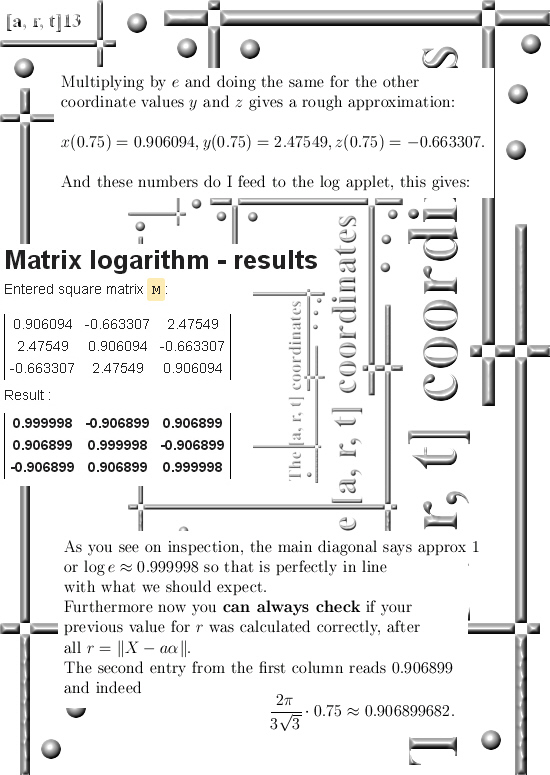
This update is 11 pictures long, all size 550 by 775 pixels.
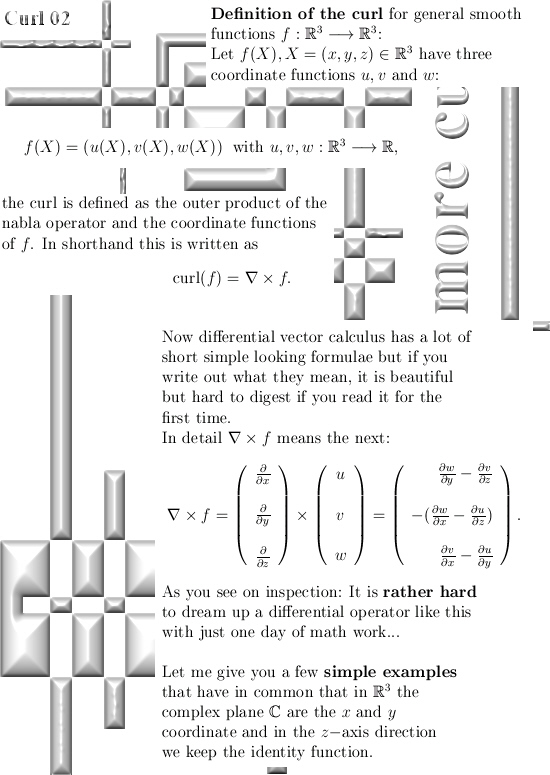
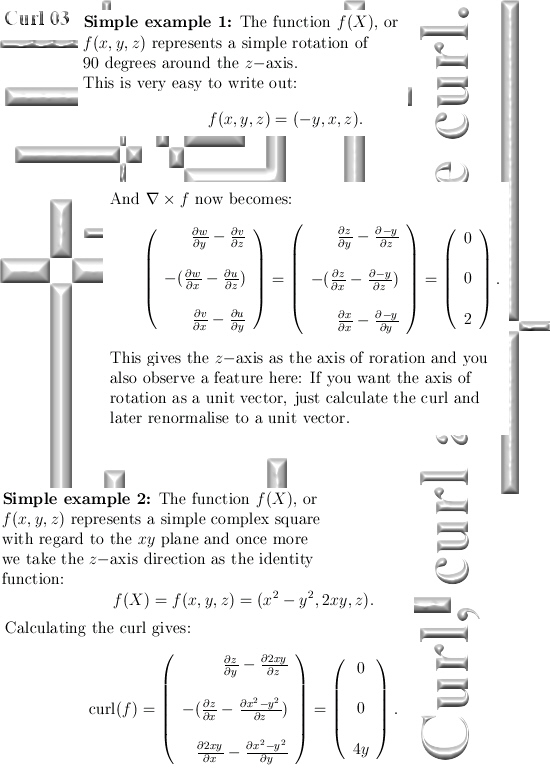
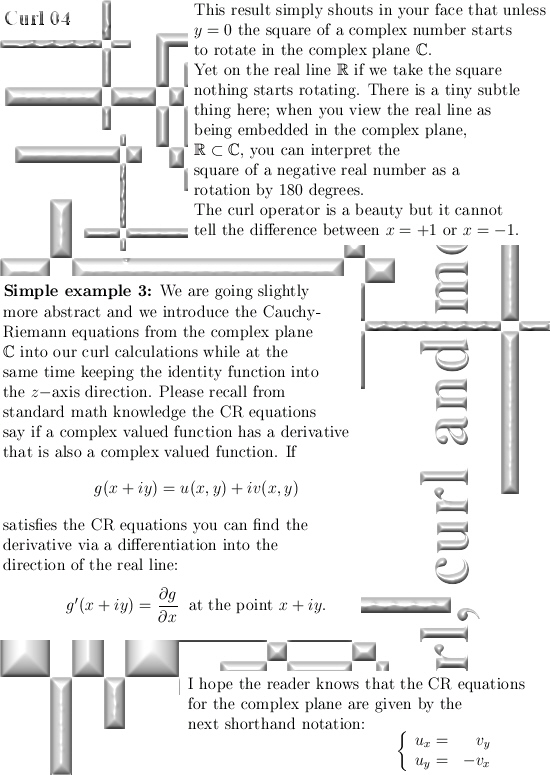
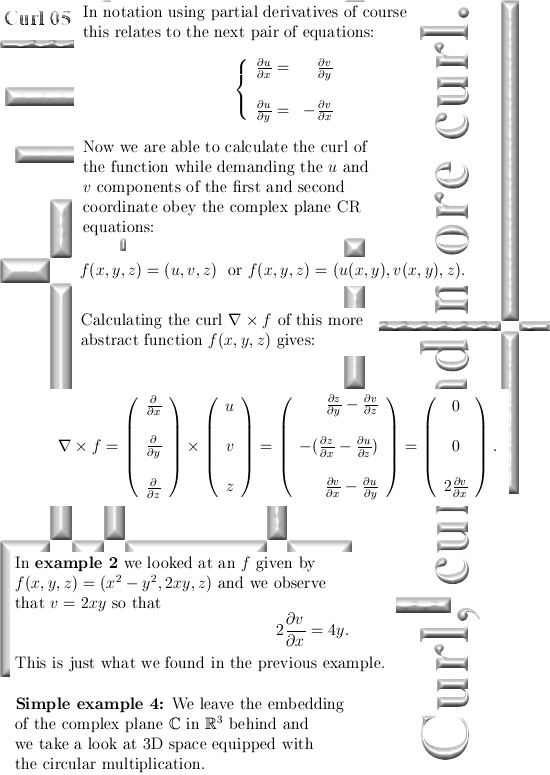
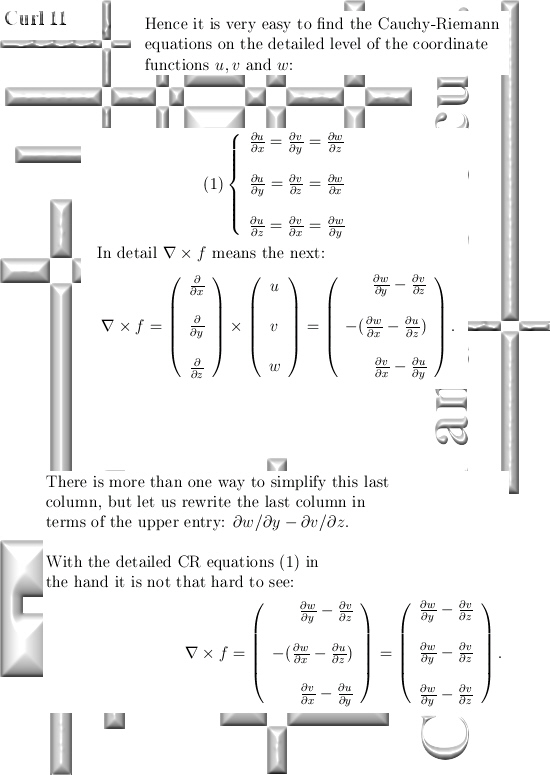
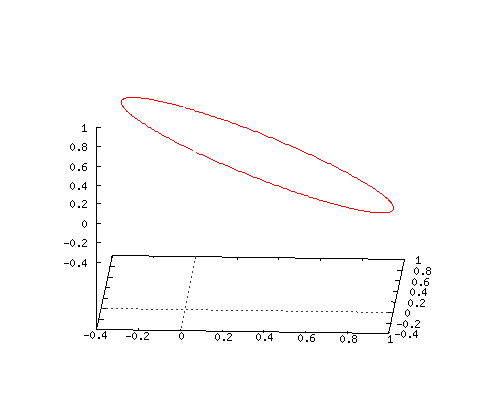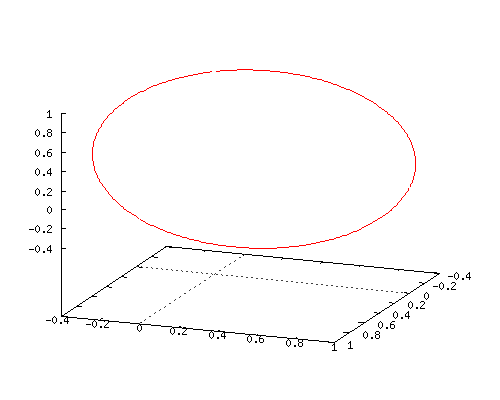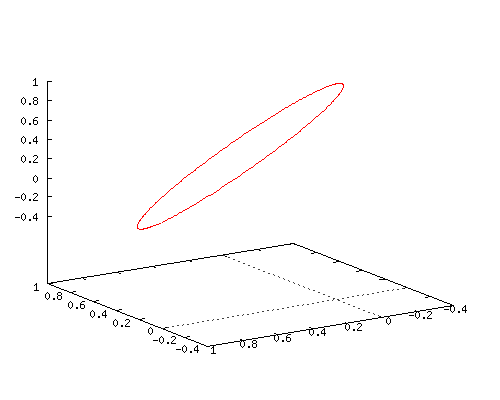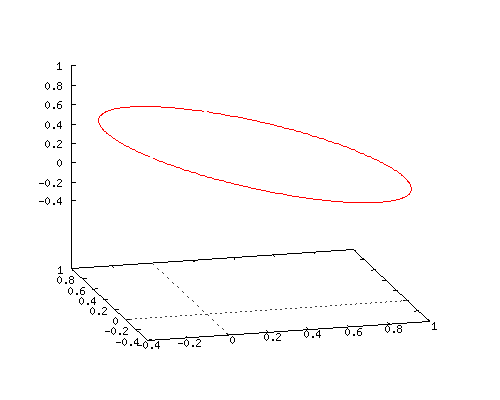
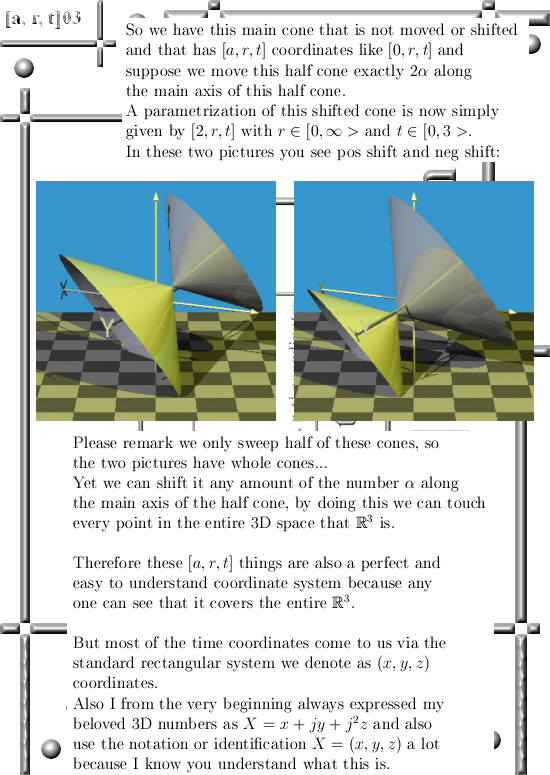
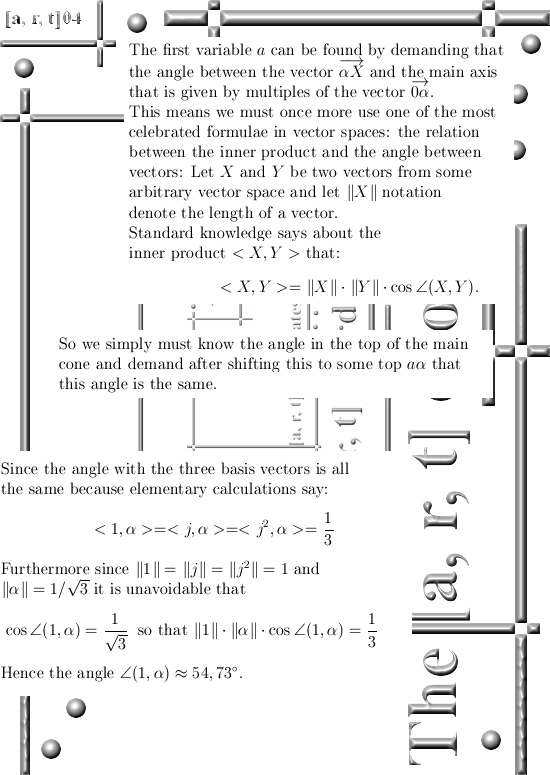
I kept the math as simple as possible and all three dimensional numbers used are the circular ones. So you even do not have to worry about j^3 = -1…

Have fun reading it:

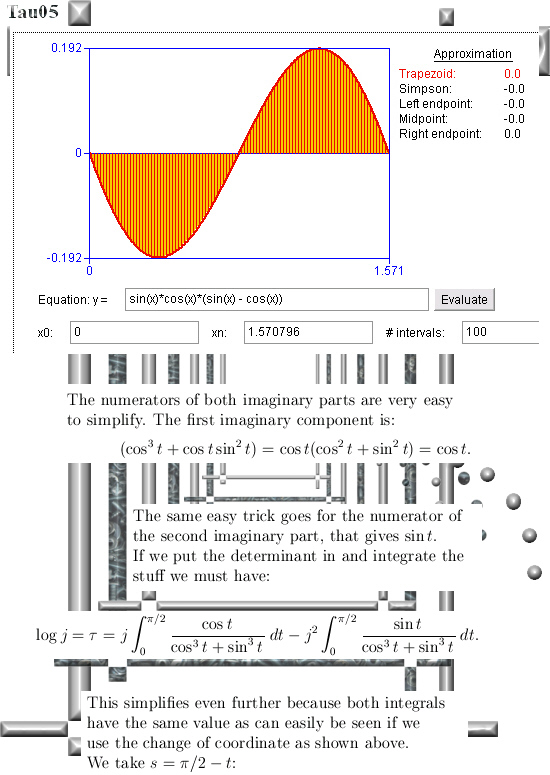
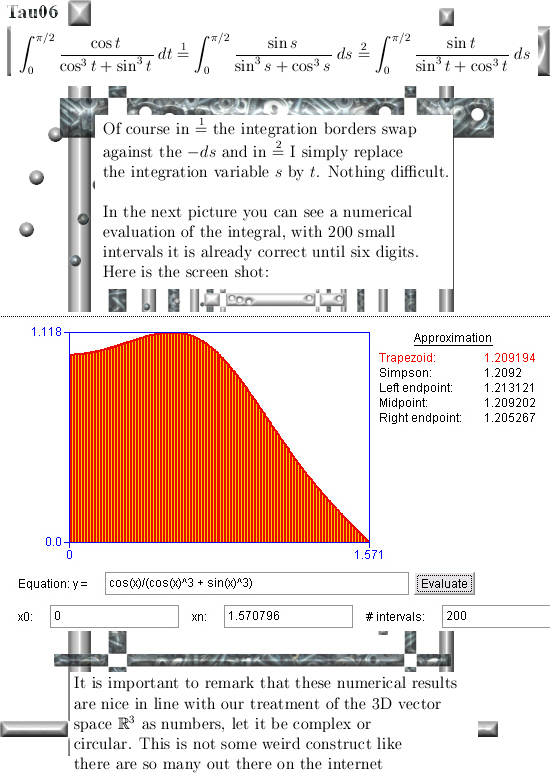
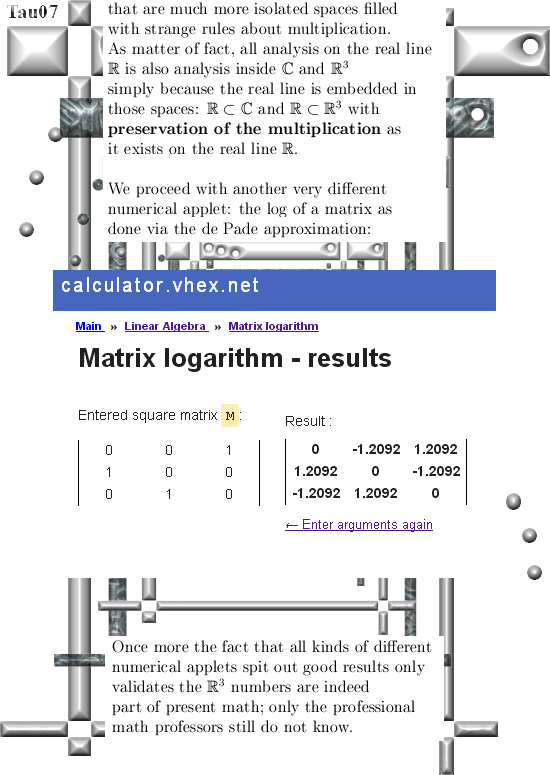
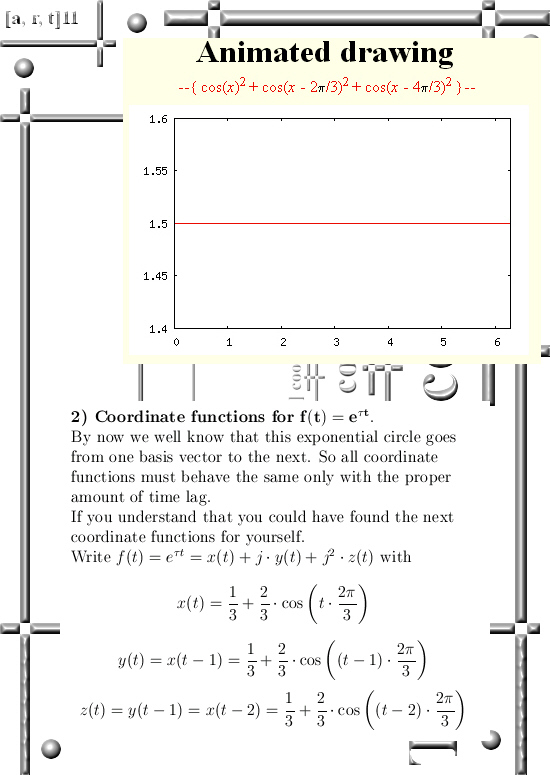
I hope you like the alternative way of calculating that integral in picture number 11. It shows that 3D complex and circular numbers are simply an extension of mainstream math, it is not weird stuff like the surreal numbers that decade in decade out have zero applications.

May be in the next post I am going to show you a weakness in the RSA encryption system.
Or may be we are going to do something very different like posting a correction on a previous post.

Let´s wait and see, till updates.

The second hybrid: a 4D mix of the complex and the circular plane.

November 24, 2016Exponential circle, Exponential curvesReinkoVenema

Update from 30 Nov: My health problems persist, my right wrist is still swollen and hot all the time. So after one week it is clear I need to see a doctor…
Anyway I can type text with one hand so here we go:

In this update I talk about the circular plane because I want to use the same language in 2D as in 3D or higher, yet for those living in the mud this stuff is mostly named split complex numbers. There are more names going round: for those people that do not understand what the conjugate of a number is and how to find those, they name it hyperbolic numbers.

This update is about finding the log of the first and only imaginary unit of the circular (also named split or hyperbolic) numbers. This mathematical goal can only be achieved by replacing the real scalars in the circular plane by numbers from the complex plane.
That replacement stuff is known in my household as the Sledgehammer Theorem, this theorem says you can more or less always replace scalars by higher dimensional numbers. But this has to make some sense; for example you have a number from the complex plane like z = a + bi, now if you replace the two real numbers a and b with general numbers from the complex plane you did not gain much. As a matter of fact you gained nothing at all because you are still inside the complex plane and other people will only laugh at you:

That is just like the way Donald Trump will expand the US economy…

For myself speaking I do not understand that a math result as in this post is more or less unknown to the professional math community. How can it be that Euler has all that stuff of finding the God formula while century in century out the math professors make no progress at all?

Every day I am puzzled by this because I am not ultra smart or so, it is only my emotional system is a bit different: I never get scared when hunting down some good math…

__________

Anyway from the mathematical point of view I am proud of this ten picture long update: it is as close as possible to the calculation that unearthed the very first exponential circle. That was the discovery that in the complex plane the log of i is given by i pi over 2.

Need a cold shower by now?

Want to restore your faith in the old masters with their superior use of math?

Try the next video from the Youtube channel, it only uses insights from the circular plane and he runs fast and far: The Lorentz boost inside special relativity:

Split complex numbers and the Lorentz boost.

Let’s leave this update with that, have a good life or try to get one.

Update from 04 Dec 2016: I would like to post the number one wiki when you do an internet search of split complex numbers. (There are all kinds of names going round, but the circular plane is also the split complex number plane for sure.)
As usual all that stuff has the conjugate wrong, but in the next wiki you see more or less the combined wisdom of the math community when it comes to expanding the complex plane to higher dimensions. (It is a dry desert, human brains are not that fit for doing math):

Split-complex number.
https://en.wikipedia.org/wiki/Split-complex_number

Once more: those people have got it wrong about how to find the conjugate and as such you can also find lots of pdf files about circular (or split-complex) numbers that say they are hyperbolic numbers.
The common fault is that they use the conjugate just as if you conjugate an ordinary complex number from the complex plane.

I remember I did that too for a couple of years until it dawned on me that we are only looking at the projections of the determinant; it has nothing to do with lengths, even in the complex plane it is not the norm of the complex number but it’s matrix representation and the determinant.

All stuff you find on this on the internet is nothing but shallow thinking.

End of this update, see yah in the next post.

The pull back map applied to the coordinate functions of the 3D exponential circle.

November 3, 20163D complex numbers, Exponential circle, Quantum mechanicsReinkoVenema

In this post, number 50 by the way, I am trying to use as elementary math as possible in order to use the pull back map from the 3D circular number system to the complex plane.

With this the pull back map and the 3D circular number system are treated so basic that with only high school math and a crash course in the complex plane students can understand what I am doing.

So for reading this post number 50, what do you need in mathematical knowledge?
1) Understand how to write cos(a + b) and sin(a + b) in terms of cos a and sin b.
2) Understanding of e to the power it in terms of cos t and isin t.
3) Understanding of the roots of unity as found inside the complex plane, in particular being able to calculate all three roots of unity when we take the third root of the number 1.

That’s all, so basically all first year students in math, physics and chemistry could understand this post at the end of their first year on a local university.

__________

The words above are only one reason to write this post; to be honest for me it took a long time to write down for the first time the coordinate functions for the 3D exponential circle.

And I never did give much solid proof for that these coordinate functions have indeed the properties as described. It all more or less came out of the sleeve as some kind of monkey trick.

Therefore for myself speaking, this post giving the results in it also serves as a proof that indeed there is only one class of coordinate functions that do the job. They can only differ in the period in time they need to go around, if you leave that out the triple of coordinate functions becomes unique.

All in all the goals of this post number 50 are:

1) To do the pull back of an exponential circle as simple as possible while
2) In doing so give some more proof that was skipped years ago.

__________

This update is seven pictures long, each 550 x 775 pixels in size.
Hit the road Jack:

I think I have nothing more to say, so see you around my dear reader in post number 51.

Till updates.

Derivation of the number tau for the circular 3D number system.

October 22, 20163D complex numbers, Exponential circle, Matrix representationReinkoVenema

There are lot’s of reasons for this update; one reason is that the actual calculation is mega über ultra cool. Another important reason is that this collection of plain imitation of how the value for the number i in the complex plane was found serves as a proof in itself that this way of crafting 3D complex and circular numbers is the only way it works.

Don’t forget that on the scale of things the Irish guy Hamilton tried for about a decade to find the 3D numbers but he failed. Yet Halmilton was not some lightweight, the present foundation of Quantum Mechanics via the use of the Hamilton operator is done so via the work of Hamilton…
Wether the professional math professors like it or not; that is the scale of things.

During the writing of this post I also got lucky because I found a very cute formula related to the so called Borwein-Borwein function. I have no clue whatsoever if it has any relevance to my own work on this website but because it is so cute I just had to post it too…

Furthermore I used two completely different numerical applets, one for integration and the other for evaluating the log of a matrix, only to show you that these kind of extensions of the complex plane to three dimensional space is the way to go and all other approaches based on X^2 = -1 fail for the full 100%.

__________

This post is ten pictures long, size 550 x 775 pixels.

At the end I will make a few more remarks and give you enough links for further use in case you want to know more about this subject. Have fun reading it.

The applet for the logarithm of a matrix can be found in this nice collection of linear algebra applets:

Linear algebra
http://calculator.vhex.net/function-index/linear-algebra

In this update you might think that via the pull back principle you observed some proof for the value of the integrals we derived, but an important detail is missing:
In 3D space the exponential circle should be run at a constant speed.
As a matter of fact this speed is the length of the number tau, you can find more insight on that in the theorem named ‘To shrink or to grow that is the question’ at:

On the length of the product of two 3D numbers.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff04.htm#06May2016

A bit more hardcore is my second proof of the value of the integrals as derived in this post. On 15 Nov 2015 I published the second proof that I found while riding on my bicycle through the swamps near a local village named Haren. It is kinda subtle but you can use matrix diagonalization to get the correct answer.
The reaction from the ‘professional community of math professors’ was the usual: Zero point zero reaction. These people live in a world so far away from me: overpaid and ultra stupid…

Integral calculus done with matrix diagonalization.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#21Nov2015

A link to the online encyclopedia of integer sequences is the next link.
Remark that by writing the stuff as on-line instead of online reflects the fact this website must be from the stone age of the internet. That is why it can have this strange knowledge…

The On-Line Encyclopedia of Integer Sequences
https://oeis.org/ (Just fill in 1, 2, 0, 9, 9, 5, 7 in order to land on my lucky day).

The last link is one of those pages that try to explain as why 3D complex numbers cannot exist, the content of this page is 100% math crap written by a person with 0% math in his brain. But it lands very high in the Google ranking if you make a search for ‘3D complex numbers’.
So there must be many people out there thinking this nonsense is actually true…

N-DIMENSIONAL COMPLEX NUMBERS.
http://www.alenspage.net/ComplexNumbers.htm

Ok, this is what I had to say. Let me close this post, hit the button ‘update website’ and pop up a fresh beer… Till updates.

Curl, curl and more curl.

September 29, 20163D complex numbers, CR equations, Exponential circle, Matrix representationReinkoVenema

This post contains seven examples of the differential operator named curl. The motivation for this update lies in the fact that after my humble opinion inside the set of equations known as the Maxwell equations there is a tiny fault: Rather likely electrons carry at least a net magnetic charge.
And because they carry net magnetic charge they not only accelerated by electrical fields but also magnetic field.

If you have an old television set with one of those fancy tubes that contain one electron cannon for a black & white television and three electron cannons for a color television. With the help of a stack of these strong neodymium magnets it is easy to give experimental proof that the electrons indeed get accelerated… Why in the course of over one hundred years not one of the professional physics professors has done this is unknown to me; may be it is the separation of ‘theoretical professors’ versus ‘experimental ones’ a reason for this omission. May be it is the use of dogma (unproven things that live inside a belief system, in this case the belief system that magnetic monopoles do not exist).

__________

Anyway the Maxwell equations contain a lot of the curl operator, that is not needed per sé but it makes the formulae look sleek and short. Originally Maxwell had a set of like 20 equations or so while at present day only four remain. But if you see those four equations for the first time it is very impressive, only over time you get used to it.

This post is 13 pictures long, size 550 x 775 pixels.
I start with examples that are as simple as possible and very slowly bring in a bit more abstraction.
Therefore I hope it is very readable, have fun with it!

As far as I can remember, in the first year I opened these investigations into higher dimensional number systems again I calculated the curl for the complex multiplication in 3D space. In this post we only looked at the circular version of stuff.

But I can´t find it back so I cannot place a hyperlink to it.

Anyway, here is a nice wiki with the curl expressed as an integral (often much harder to calculate but nice to observe it can also be done that way):

Curl (mathematics)
https://en.wikipedia.org/wiki/Curl_(mathematics)

And because this post was motivated by all that curl in the Maxwell equations, I tried to find back when I originally started writing about electrons having magnetic charge instead of being magnetic dipoles like they are tiny bar magnets. It was 29 April that inside the math pages I found the first update on that. Here it is:

From 29 April 2014 : Do electrons have spin?
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#29April2014

Ok, that was it. Till updates my dear reader.

How I found the first modified Dirichlet kernel in 5D numbers.

July 7, 20163D complex numbers, 5D complex numbers, Exponential circle, Exponential curves, Matrix representation, Quantum mechanicsReinkoVenema

Back in Jan 2014 I was able to solve the circular and complex 5D numbers systems using the so called ‘tau-calculus’. Basically tau-calculus is very easy to understand:

Find a basis vector (from an imaginary number) that has determinant +1.
Craft analytical expressions that you cannot solve but use internet applets for numerical answers. Or, equivalent:
Use an applet to calculate the logarithm of your basis vector once you have put it on a matrix representation.
Start thinking long and hard until you have solved the math analysis…

This is easy to understand but I could only do this in three and five dimensional space, seven or eleven dimensional space? It is now 2.5 years later and I still have no clue whatsoever.

Anyway back in the time it was a great victory to find the exponential curves in 5D space. May be some people with insect like minds think that the Euler identity is the greatest formula ever found but let me tell you:
The more of those exponential circles and curves you find, the more boring the complex plane becomes…

In the months after Jan 2014 I wanted to understand the behavior of the coordinate functions that come along those two exponential curves. But the problem kept elusive until I realized I had one more round of internet applets waiting for me.
I had to feed this internet applet for the log of a matrix over 50 matrices and write down the answers it gave me; that was a lot of work because every matrix had 25 entries.

Originally I planned for ‘digesting’ 10 matrices a day so it would be a five day project, but when I finally started somewhere in June 2014 after two days I was ready to sketch my strongly desired coordinate function of the very first coordinate in 5D space.

I still remember sitting at my table and do the drawing and when finished it was so fast that I realized the next: This is a Dirichlet kernel.

And the way I used it, it was so more simple to write down this kernel and if you think how those exponential curves in higher dimensional spaces work with their starting coordinate function and all the time lags that follow… This finding will forever be in the top ten of most perfect math found by your writer Reinko Venema…

__________

Ok, what is in this new post?
Nine pictures of size 550 x 775 pixels containing:
Basic definitions upon 5D complex and circular number &
Tau calculus for the exponential curve &
Explaining how I found the graph of the first modified Dirichlet kernel &
A small quantum physics example related to probability amplitudes &
Some cute integrals that are easy to crack now.

Hope you can learn a bit from it, do not worry if you do not understand all details because even compared to the 2D complex plane or the 3D complex numbers this website is about:
The 5D realm is a space on it’s own!

Have fun reading & thinking upon it:

A few links of interest are the next:

You need a good applet for the log of a matrix representation if you want, for example, crack the open problem in tau calculus for the 7D complex numbers:
http://calculator.vhex.net/calculator/linear-algebra/matrix-logarithm

My original update on the other website about the 5D number systems from Jan 2014:
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#30Jan2014

If you are more interested in those kind of weird looking integrals suddenly easy to solve if you use a proper combination of geometry and analysis, the update from July 2015 upon the missing equations is also worth a visit:
The missing equations.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#14July2015

__________

This is what I more or less had to say, have a nice life or try to get one.
See you in the next post.

Modified Dirichlet kernels for low dimensions.

June 20, 20163D complex numbers, 5D complex numbers, Exponential circle, Exponential curvesReinkoVenema

What the hydrogen bomb is in the average nuclear arsenal, that is what modified Dirichlet kernels are for higher dimensional complex & circular number systems.
Via the so called tau calculus I was able to achieve results in 3 and 5 dimensional number systems and I really had no hope in making more progress in that way because it gets so extremely hardcore that all hope was lost.

Yet about two years ago I discovered a very neat, clean and very beautiful formula that is strongly related to the Dirichlet kernel known from Fourier analysis. The formula I found was a dressed down version of the original Dirichlet kernel therefore I named it ‘modified Dirichlet kernel’.

This modified kernel is your basic coordinate function, depending on the dimension of the space you are working in you make some time lags and voila: There is your parametrization of your higher dimensional exponential (periodic) curve (only in 2D and 3D space it is a circle).

For myself speaking: this result of finding the modified Dirichlet kernel is for sure in my own top 10 list of most important results found. Not often do I mention other mathematicians, but I would like to mention the name of Floris Takens and without knowing how Floris thought about taking a sample of a time series and after that craft time lags on that, rather likely I would not have found this suburb and very beautiful math…

__________

I haven’t decided what the next post will be about.
It could be stuff like:

How I found the first modified Dirichlet kernel, or
Wirtinger derivatives for 3D number systems, or
Wow man, can you factorize the Laplacian operator form Quantum Mechanics???

But factoring the Laplacian requires understanding 3D Wirtinger derivatives so likely I will show you how I found the very first modified Dirichlet kernel.

__________

This update contains six jpg pictures each about 550 x 775 pixels and two old fashioned animated gif pictures. I tried to keep the math as simple as possible and by doing that I learned some nice lessons myself… Here we go:

This is the animated gif using z = 0 in 3D while this picture is showing the Euler exponential circle:

Here is an animated gif of how this coordinate function looks when you combine it with the two time lags for the y(t) and z(t) coordinates. Does it surprise you that you get a flat circle?
If it does not surprise you, you do not understand how much math is missing in our human world…

In case you are interested in the ‘time lag’ idea as Floris used it, here is a nice Youtube video that gives a perfect explanation. If you apply this time lag idea for example is a 17 dimensional real vector space you get a 17D exponential curve with all of it’s magnificent properties…

Takens’ theorem in action for the Lorenz chaotic attractor

Yes, end of this post. See ya around & have a nice life or try to get one.

Three centuries after de Moivre finally some new baby steps.

June 5, 20163D complex numbers, Exponential circleReinkoVenema

I am a little bit late with this post but after the previous post I took some time to enjoy it because not every day you can craft a brand new coordinate system…

Also I was a bit in doubt about this post, shall I finally start with those modified Ditichlet kernels or work out a simple de Moivre example in 3D? It became the latter so likely in the next post I will do some first things with modified Dirichlet kernels.

This post is just 4 pictures long (size 550 x 775 pixels) and to be honest it contains no serious math whatsoever. I was only driven by curiosity about how difficult a simple example of the new 3D versions of it would be.
Now it is not 100% trivial but it is also not a very deep result, at best you can say it is a bit technical because you constantly have to apply those sum and difference formulae for the cos and sine functions.

The real deep math work was crafting those exponential circles in 3D in the first place and later finding the coordinate functions belonging to that. That was the deep math because once you have those, the new de Moivre formulae are a piece of cake (make sure it is gluten free!).

__________
In this update I also would like to make an advertisement for a long update I started about one year ago on the other website; all in all it is 37 pictures long (size 550 x 1100) and it took about 3 weeks to write it. It has the title The Missing Equations because with those modified Dirichlet kernel I knew I had solved a terrible hard problem but the higher in the dimensions I got the more missing equations I had for my wonderful solution… Here is the link:

From 14 July 2015: The missing equations.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#14July2015

__________

After this small advertisement here are the four pictures of this update:

Once more: This is not a deep mathematical result or so.
I was just curious of how difficult it would be to get one of the most simple 3D new de Moivre formula results using only the 3 century old stuff from about 50 years before Euler entered the scene…

The most important lesson you can learn from this is that instead of focusing on all kinds of details like n = 2 and only the real part and so on is a waste of time and energy.
After all using the exponential circle is what brings peace to the heart; it is simple, it covers all powers at the same time and you have all coordinate functions at once…

__________

Now you have to wait a few minutes more because I would like to pop up a fresh home brew and after that I will hit the ‘publish post’ button…

Thanks for the waiting 😉 Now I will hit the publish button and see you next time around!

The new 3D coordinate system; [a, r, t] coordinates.

May 24, 20163D complex numbers, Exponential circle, Matrix representation, Quantum mechanicsReinkoVenema

About a full week late all is now finished. Also there was that problem of the hacked webpage; the third update on the Schrödinger equation was loaded and loaded with all kinds of weird comments. But if you did read those comments you could see the overwhelming majority was not written by humans but were posted by bots.

Anyway in the end even advertisements for online sales of viagra and stuff surfaced so I took an evening to see if this could be repaired. For the time being it is not possible to post comments although before it was also impossible but that was due to an unknown technical fault…

__________

In this update we dive into the [a, r, t] coordinate system and this is very similar to using polar coordinates in the complex plane only in 3D we are moving a half-cone along a line and as such sweep through the entire 3D space. In short it goes like this:

With a we control how far the cone is moved from the origin,
with r we denote the distance from a particular point X to the top of the cone and finally,
with t we figure out how much we need to rotate stuff using an applet for the log of a matrix.

I also give once more the coordinate functions of the exponential circle so that you are able to find coordinates on the main cone (that has the origin as it’s top) for yourself.

Without prove I also give a new de Moivre formula, the original de Moivre formula is from about 50 years before Euler so after 3 centuries there is a bit of moving forward on that detail.

I also give a rather strange looking sum of squares of cosine functions that add up to 1.5; the three cosine functions all differ by 120 degrees or 2pi/3 if you want.

It is important to remark I did my best to keep it as simple as possible so I also concentrate on a few worked examples so it is not just theory but also how to find these new coordinates. In relation to other posts like the Schrödinger equations posts, I think this new coordinate system is definitely of interest to people from quantum physics and chemistry that try to calculate those atomic and molecular orbitals.

This update is relatively long: 14 pictures of size 550 x 775 pixels and for the first time I use unshrunk jpg pictures because year in year out the bandwidth of internet connections is still rising fast so why remove fine detail from jpg pictures any longer?

__________

I hope you learn something new, here are the pics:

Ok, that was it. For myself speaking I more or less expect everything to be the same:
Professional math professors from around the globe will keep on talking about their own research and just how important it is to use complex numbers from the complex plane.

A few useful links:

De Moivre’s formula
https://en.wikipedia.org/wiki/De_Moivre’s_formula

And a good applet for the logarithm of matrix representations is also handy:

http://calculator.vhex.net/function-index/linear-algebra
http://calculator.vhex.net/function-index/linear-algebra

And last but not least is a proof for the latest formula above: the circular multiplication on the [a, r, t] coordinates can be found on the other website:

From 06 May 2016 : On the length of the product of two 3D numbers.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff04.htm#06May2016

Let’s leave it with that. Till updates.

An important correction on a very very stupid typo…

May 19, 20165D complex numbers, Corrections, Exponential circle, Matrix representationReinkoVenema

Let’s not do difficult: there are typo’s and there are typo’s.

The one kind is for every body directly to understand ‘this is a typo’ and the brain pops up what should be the correct thing standing there.

And there is that kind of typo that is a disaster in people trying to understand what this stuff actually means.

I am sorry I messed things up, but it is like picture six on the previous update on the length of complex numbers that must have been a root cause of much disunderstanding.

In the next picture I show you the correction: in that matrix it now reads log r instead of only r.

Why I was that stupid a few weeks ago is non of your business, but by now stuff is repaired and we no longer have this horrible mistake around any longer…

Ok, let’s leave it with that. Till updates.

3Dcomplexnumbers

Math as you have never seen before…

Category Archives: Exponential circle

Some very rudimentary Fourier stuff + a surprising way to do a particular integral.

The second hybrid: a 4D mix of the complex and the circular plane.

The pull back map applied to the coordinate functions of the 3D exponential circle.

Derivation of the number tau for the circular 3D number system.

Curl, curl and more curl.

How I found the first modified Dirichlet kernel in 5D numbers.

Modified Dirichlet kernels for low dimensions.

Three centuries after de Moivre finally some new baby steps.

The new 3D coordinate system; [a, r, t] coordinates.

An important correction on a very very stupid typo…