I wrote this post because I was curious how the world famous +/- pattern would look in case you try to do what the title of this post says. I focussed on the first two columns and there are six 2×2 minors to be found there. May be in the future I will use the result from this post in more writing around the theorem of Pythagoras for nxd matrices where the first d columns of a matrix are also a parallelepipid of dimension d. And if done properly, after making the nxd a square matrix, you can take the determinant in the way of this post and get the d-dimensional volume of the parallelepipid.
Well, we’ll see because yes you get that volume but you don’t get a proof of the matrix version of the theorem of Pythagoras for such nxd matrices.
This post is as simple as possible so if you understand the 4D case I expect you to also grasp how to generalize this to arbitrary dimension. The post is five picutes long and it is handy to have the permutation variant of calculating a determinant in the back of your head. In case you never did see that before, shame on you but you can’t help it if you are some victim of the American educational system… Here’s a link: https://en.wikipedia.org/wiki/Determinant.
Ok here are the five picture for this post:
As you see: grouping this as six minor determinants multiplied against the determinant of their duals is a handy way to get all those 24 terms of each four factors a 4×4 determinant has. That was it for this math post, likely the next post is one more on magnetism and all those experiments around the so called Bell theorem. We’ll see but anyway thanks for your attention and may be see you in another post.
Lets me start with my question for you: Likely more than once you have seen a depiction of a photon in terms of it’s electric and magnetic field. And always the magnetic field and electric field are very similar, see for example the first picture below. That is my understanding of a linear polarized photon: It has it’s maxima, minima and zero’s on the same place.
Photons can be made by electrons for example when they accelerate. The official version of the electron is that it is a ‘tiny magnet’ and as such not a magnetic monopole as I think it is. My question is very simple:
If it would be true that an electron has two magnetic poles and is an electric monopole, then how come the electric and magnetic field in a photon are so similar?
That is kind of weird and after a decade of looking at explanations of magnetic stuff by physics people I know that always when something a weird or outright crazy, it is always ignored. They only tell things that at the surface sound logical and all weird stuff simply gets neglected. There are many examples of this, one of the main examples is the electron pair in chemical bonds. The official theory says their spins must be anti-aligned but elementary insights in magnetics say that now the potential energy is maximal while in general nature always strives to the lowest potential energy state. And try to hold two bar magnets with the same poles at each other and it repels: Well the weird things about electron pairs always get skipped by the professional physics professors…
Anyway, below is my understanding of two linear photons made by two electrons with a different magnetic (monopole) charge. I have left out all details that are not needed like the speed of light or the frequency. That is because I want to highlight the difference in the magnetic component they have: A phase shift of pi or 180 degrees if you want so.
So far for the question I had for you. The video is from Qiskit, that’s IBM, and in the quantum computer world David DiVincenzo is a celebrated name. Back in the nineties together with another person he posted some criteria for making something as say a qubit based on the spin of the electron. He has been working of stuff like this for about three decades now, of course there is no working qubit based on electron spin at all and of course David has no clue at all as why this is but like all university people he is extremely good at talking out of his neck.
I took the freedom to make a few screenshots and in the middle of the image below you can see David has strong mathematical fantasies about how such spin qubits should behave. Well David, if you ever read this: Likely they won’t do that in a billion years.
For example in the entiry video of one hour long David never ever touches the delicate detail of how to flip the spin of an electron. Now of course you can always apply a magnetic field and say that the electron will align itself with that magnetic field because it has a torque on it by this magnetic field. On the other hand official quantum theory says that alignment or anti-alignment is fundamentally probabilistic. So this is a problem and people like David never have such problems. Or at least they don’t talk about it…
At last the video, it is a bit long and not suitable for a tiktok video.
Ok, that was it for this post on magnetism. The next post is a math post on how to express the determinant of a 4×4 matrix in terms of a bunch of 2×2 minor matrices. Thanks for your attention.
Yes I know the name “Cross Product” is not correct because most people think a product has to do with two things or more formal: A product has two arguments. On the other hand this method of calculating a vector perpendicular to a specific triple of vectors in 4D space is a clear cut extension of the widely known and used cross product in 3D space.
At first when I started writing this post I only wanted to bring a bit more clarity of why it is handy to just use the famous +/- checker board pattern like you must in the inversion of a square matrix, but when I finished it even I considered it just too simple. And yes I always try to make it “As simple as possible” but I wanted a tiny bit more so called “math bone” to it so that’s why I wrote the rest of this post.
And in the rest of the post I show you how to make a 3D vector into a 3×3 matrix such that the determinant is the length of the original vector, this is done in two ways. I used stuff like that a few years ago when we looked at the matrix version of the famous Pythagoras theorem. So at the end I will link again that beautiful pdf from Charles Frohman upon that subject of a Pythagorean theorem for non-square matrices.
I also included a simple way to see why this method of finding or calculating a new column that is always perpendicular to all other columns to the left of it works. Originally I just took it from the way you calculate the inverse of a square matrix.
So that’s more or less it, the post is six pictures long and at the end the pdf upon that Pythagoras thing. I made a fault in numbering the pictures but I am to lazy now to repair it. It should read 01/06 and not 01/07…
All that is left is place the link to the pdf. The pdf is roughly made of three paragraphs, the first one is the most important while the second paragraph are for crafting a bit theory to finally prove the theorem in the third paragraph.
This video shows that in all likelihood quantum computers will never work, anyway not when it comes to simulating chemical reactions where electron pairs play a role. Let me explain: The SG experiment is of course the Stern-Gerlach experiment from 1922 for readers who do not know that. That was the experimental discovery of electron spin although Stern and Gerlach wanted to prove something very different. Now as far as I know a repeated SG experiment, or a sequential experiment, has never been done. Likely it has been tried a few times but as far as I know nobody succeeded into getting the desired results and as such proving the probalistic nature of measuring electron spin. Since 2015 I have been looking for this but until now I found nothing. In this video at about 08:09 min into the video Katie claims that after the original SG experiment from 1922 countless experiments have been done where a sequence of such experiments was done. See the image below, the Z and X just denote the derection of the applied magnetic field. These kind of experiments just have no result. In video’s like this you always hear the names of Stern and Gerlach but never ever the folks who would have done such a repeated experiment.
And again for readers unfamiliar with what I think of electron magnetism, I think that electron magnetism is just as electron electricity: It is a monopole and permanent charge. So there are two kinds of electrons that have the same electric charge and opposite magnetic charges. On top of that I think the magnetic charge is permanent so it can’t be flipped and measuring the spin is not a probabilistic event. It’s permanent… I made a few screenshots from the usual nonsense in the sense it is not rooted in experimental evidence:
For myself speaking I do not understand why so many people think that these experiments are actually done. Since I was a bit annoyed by the video, with a simple internet search in only a minute or three I found a nice pdf from MIT the Open Courseware stuff. Let me quote from page 5:
Let us now consider thought experiments in which we put a few SG apparatus in series.
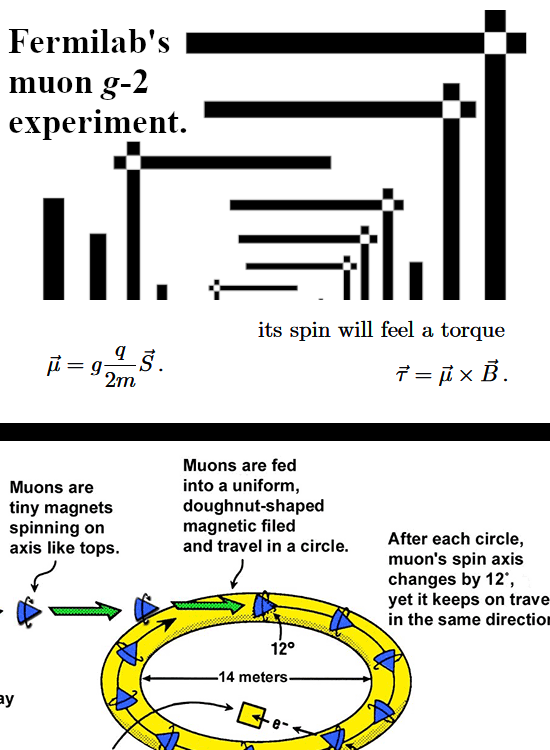
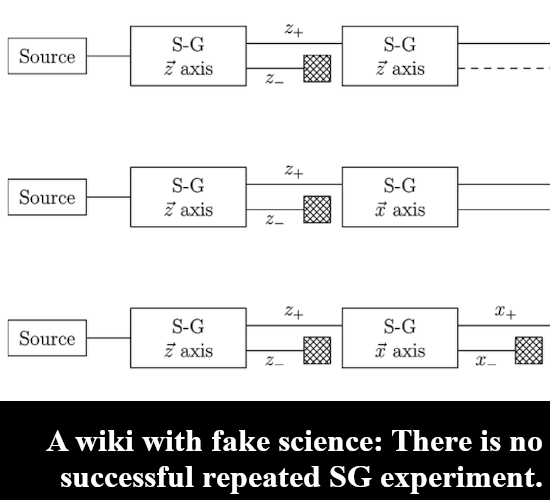
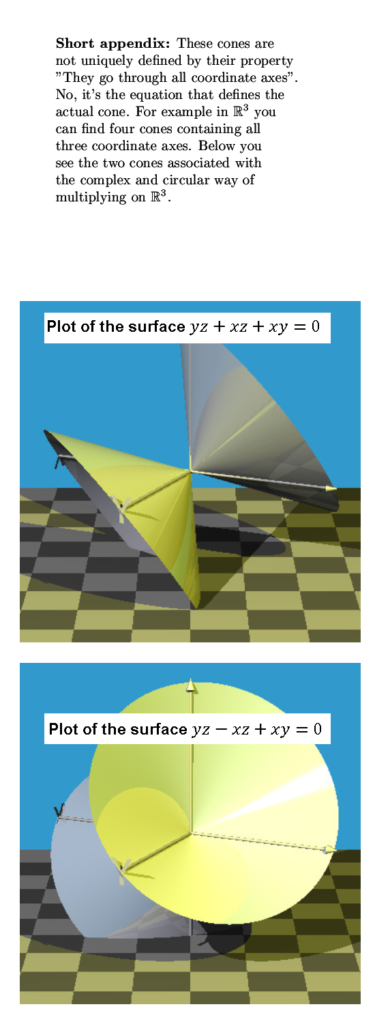
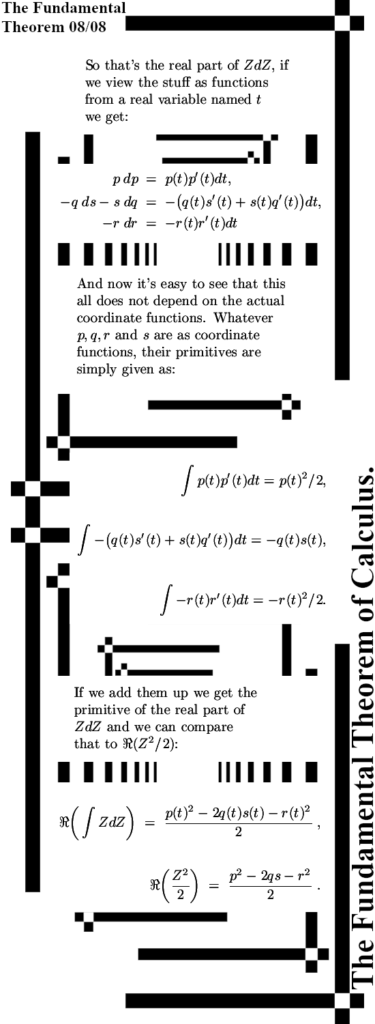
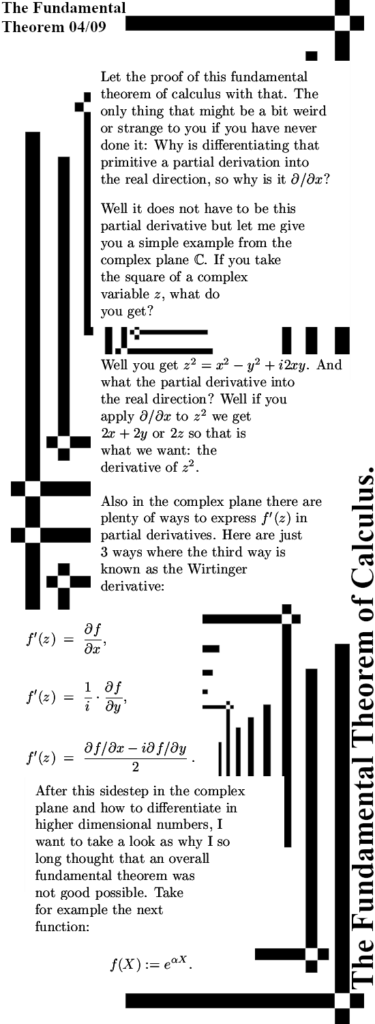
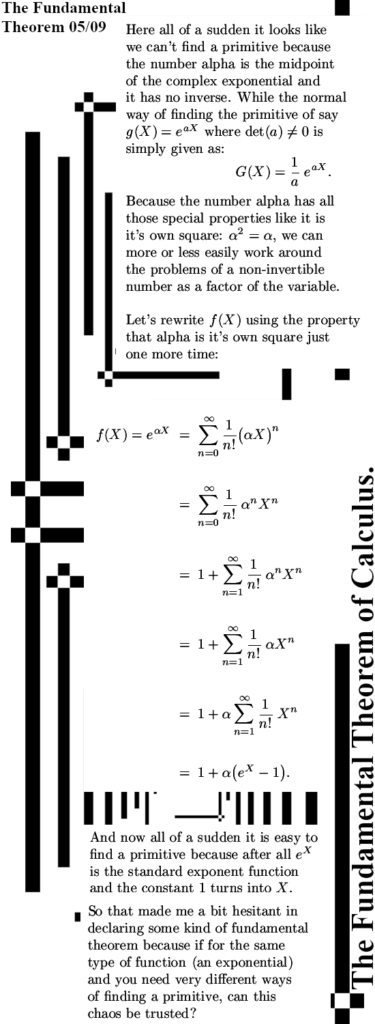
To focus the mind and or for new readers; I am of the opinion that electrons are magnetic monopoles and that their magnetic properties are just as the electric properties: permanent and monopole.
Well that is very different from the official version of electron magnetism that involves the Gauss law of magnetism that says magnetic monopoles do not exist and as such the electron must have two magnetic poles. There are a plentitude of what I name weird energy problems with bipolar electron magnetism. For example what makes an electron anti-align with an applied external magnetic field? If you look at it that way, it is easy to find much more weird energy problems and the main example I always use is the electron pair. For example molecular hydrogen is has one bonding electron pair and it’s spins must be opposite or anti-aligned as the wording goes. Well, what explains that this is the lowest energy state? And how can H2 be stable with a magnetic configuration like this? Bar magnets are only stable and in a state of low potential energy if their magnetic fields are aligned, so why is it opposite with the two electrons in an electron pair? If you view electrons as having a monopole magnetic charge, you never run into those problems that are always skipped when in experimental results electron magnetism plays a role. It is just always skipped, look at any explanation of the Stern-Gerlach experiment and you never see it explained as why electrons anti-align with the applied vertical magnetic field.
But lets go to the video: Fermilab’s Don Lincoln explains how an entangled electron pair should behave. Of course he does not have any experimental evidence to back up all the stuff he claims. For 10 years now starting back since 2015 I have been searching for a repeated Stern-Gerlach experiment but there is only talking out of the neck and no results anywhere. Now a repeated SG experiment is just applying differently oriented magnetic fields to an electron and the official theory says that the probability for spin up or down is the cosine of half the angle of the difference in ortientation of the two succesive magnetic fields. So it looks a lot like linear polarization of photons only there you have the entire angle and not half the angle.
Since I became interested in electron magnetism 10 years ago I have seen a few hundred video’s on all kinds of stuff related to electron spin. Also those long video’s of say one hour or longer where researchers explain what they are doing. And often in those presentations there are some theoretical curves and with litle dots or squares the experimental results are given to the audience. So what Don Lincoln is doing in the video is rather misleading; the curves is just the square of a cosine but there are no experimental results as far as I know.
This is pretending experimental results…
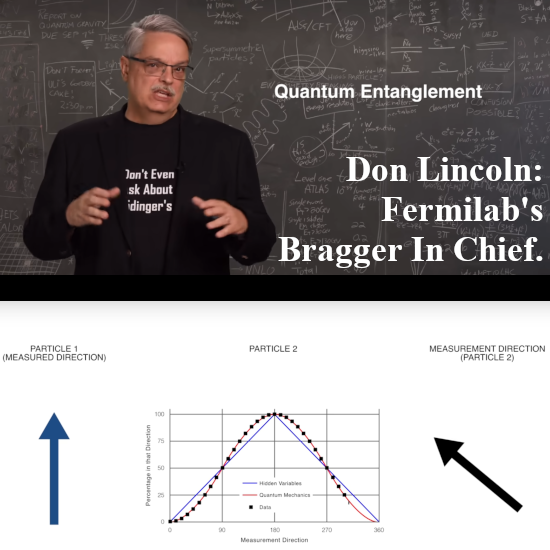
I think it was two years back or so that a few Nobel prizes were handed out and one of the recievers Alain Aspect remarked in a video that is was just to hard to do this experiment with real spin half particles like electrons. As such Alain did his experiments with photons. Don Lincoln even shows a picture of Alain and because most physics people always talk out of their neck when it comes to electron spin, he does the entanglement thing with electrons. In this video he does not brag that physics is a so called ‘five sigma’ science where all stuff is validated rigidly. So here is the video in case you are interested in that so called non-locality stuff:
Ok, I have more to do today so let me close this short post on the ususal nonsense of official electron spin.
In this post I want to look at three experiments from physics that all use a vertical magnetic field that is applied to unpaired electrons. The three experiments are: 1) The famous Stern-Gerlach experiment from 1922. 2) The Einstein-de Haas effect. 3) The muon g-2 experiment from Fermilab.
And the two criteria I use is also simple to understand: 1) Are there weird energy problems? 2) Is the electron spin alignment probabilistic yes or no?
You might think “Why should that have any importance at all?” Well the importance lies in the fact that all official explanations for the outcomes of the 3 above mentioned experiments, if you think about it, they all exclude each other.
For example the Stern-Gerlach experiment is often used to point at the probabilistic nature of measuring the direction of electron spin. And it is the 50/50 split in the beam of silver atoms that is the actual evidence of the fundamental probabilistic nature of measuring electron spin with a vertical magnetic field. But in that Einstein-de Haas effect experiment, the results are always explained by all electrons doing the same and it is impossible to find the word “probabilistic” in such explanations. To focus the mind a little bit: If you would have a 50/50 probability in spin alignment with the applied vertical magnetic field, in that case there would be no Einstein-de Haas effect at all. Now what is a weird energy problem? For me it is as simple as the so called anti-alignment of electron spins. It is kinda weird that half of the electrons would align their spins and as such lower their potential energy and the other half weirdly raises their potential energy? Please remark this simplest form of a weird energy problem is a direct consequence of viewing electrons as bipolar magnets, if you skip that assumption and view electrons as magnetic monopoles you do not have this simplest of energy problems. The post is four pictures long and I hope I won’t forget to place a few links to the three experiments although it is very simple to do that yourself. So lets go.
Ok, that was it more or less. So the 3 experiments might be about electrons in some vertical magnetic field, the explanations vary widely. Let me close with a few links to the 3 experiments.
Link 1: A wiki about the Stern-Gerlach experiment: Stern–Gerlach experiment. Link used: https://en.wikipedia.org/wiki/Stern%E2%80%93Gerlach_experiment
Halfway in the wiki they show the so called repeated SG experiments, the problem is that for 10 years now I can’t find anyone who did a successful repeated SG according to the stadard theory. But in the wiki the authors seem to think, just like a lot of physics professors, that such repeated experiments have been done. But if it had been done, that would validate the probabilistic nature of quantum mechanics when it comes to electron spin and as such the person(s) who did that experiment would have gotten a Nobel prize for that. As far as I know, there is no Nobel prize handed out for such a thing, anyway I never heard of it. So the next picture is total scientific crap as far as I know:
Link 2: The Einstein-de Haas effect. Again a standard wiki:
Einstein–de Haas effect Link used: https://en.wikipedia.org/wiki/Einstein%E2%80%93de_Haas_effect
In order to show the source of the quote in picture 03 of the main text above, here is the quote once more: Therefore, in pure iron 96% of the magnetization is provided by the polarization of the electrons’ spins, while the remaining 4% is provided by the polarization of their orbital angular momenta.
That abundantly shows they think all electrons do the same.
Link 3: I did some arbitrary choice on the preprint archive about the last results of Fermilab with their g-2 experiment. My main problem with their explanation is of course that while using a vertical magnetic field, they claim the muon spin stays horizontal. So what happens to the good old torque that this vertical magnetic field does remains a mystery. And the pdf from the preprint archive is not that important but I want to show it to you so you can read it yourself and conclude that this all is left out and you get a bunch of hard to understand gibberish.
When reading some old texts I found that in the past I named this theorem the Scalar Replacement Theorem and that is may be a better description of the stuff involved. The Sledge Hammer theorem says that if you have say a 3D complex or circular number, you can always replace the reals by numbers from other higher dimensional system. I took the 3D circular numbers, so the third power of the first imaginary unit equals one, and replaced the real x, y and z by the 2D complex numbers from the complex plane. Of course you know that in the complex plane the imaginary unit i squares to minus one so if we replace the reals by 2D complex numbers we get a 6D number system.
The Sledgehammer Theorem says that if you do that, the newly formed 6D number system commutes and if you want you can find the Cauchy-Riemann equations that belong to this particular set of higher dimensional numbers. This is the very first hybrid number system I crafted, it is hybrid because it is not circular nor complex but has imaginary units that are different in that detail.
The main goal of this post is to show that both imaginary units commute and that makes the whole 6D number system commute. I concentrated on two different ways of making a matrix representation and I kept it that way. So the simple to understand thing that ij = ji is the main goal of my new post but from experience I know that for other people it is always amazingly hard to find a conjugate. On the complex plane it is just a flip in the real axis and for some strange reason people always do that and end up with rubbish in say spaces like the 3D circular numbers. Therefore I took the freedom to include the conjugate and of course if you have the conjugate why not try to extract a bit of cute math like the sphere-cone equation from it and see how this looks in this 6D hybrid number system.
The post is seven pictures long and one appendix so all in all eight pictures of size 550×1500 pixels. I tried to keep it all as simple as possible but hey it’s a 6D space made from a 3D circular space and a 2D complex space. Have fun reading it.
And I made a tiny appendix upon those cone like structures. Only in 3D it is a proper 2D cone of course. It is only to show that a cone is defined by it’s equation and it has the property it goes through all coordinate axes. Even in 3D space there are four cones that include all coordinate axes, I show you the cone associated with the complex and circular 3D spaces.
That was it for this post that despite it’s rather limited math content grew a bit long after all. In case you haven’t fallen asleep right now may I thank you for your attention. May be we do a good old post on magnetism as the next post or just somehting else. I don’t know yet so we’ll see.
It is already some time ago that I posted the last part of the new ‘General Theory’ series. That was on Oct 28 in 2023 and the last part was about the Cauchy-Riemann equations for n-dimensional real space aka the n-dimensional complex and circular numbers. Since the CR equations govern anything related to differentiation, how to calculate partial differentials and how they relate to each other and most of all: how to find the derivative of a function, you will need that to understand this post. This post is the fundamental theorem of calculus and that is of course integration along a contour of as I often name it a bit wrong ‘line integration’. Basically the result is the same in all spaces: Under certain mild conditions you can integrate along a contour some function that we name f. And if you do that the result is the difference of some primitive lets name it F in the end points of that curve of integration. Now in the last post on integration where we looked at the fundamental theorem of calculus for the 3D complex numbers I pointed at the fact it is now the year 2025 and why did it take so long? Well all those years I assumed that getting a primitive F of some function f was not always assured especially when you were integrating in the sub spaces of non invertible numbers that higher dimensional numbers have. And yes there are a boatload of troubles there, sometimes it is very hard to find a primitive and it is not always clear if you will actually find it.
So in this post I turned the troubles upside down and I simply start with a primitive and it is proven that the integral of the derivative of this primitive is the primitive. To put it simple: 1) I have some primitive F or F(X), 2) I differentiate it to get some f or f(X) and 3) I integrate along a curve from A to B and guess what? 4) I get F(B) – F(A).
But by doing that, how to find the derivative inside the sub space of non-invertible numbers? After all you can’t devide by then so how to even make sense of the most basic limit for calculating the derivative? From the ‘math technical’ side of things, this was easy to solve with just a tiny modification this division by a non-invertible number can be avoided. With that this approach of starting with a primitive looks like a clean approach without much unsolved problems of understanding. Weirdly enough it was a easy ‘do-able’ so by just differentiating the set of all primitive functions I could avoid proving the existence of primitives when you take the integral of some function f.
The post is six images long and have size 550×1500 pixels, there are an additional two images in the appendix where I work out the primitive of ZdZ in the space of 4D complex numbers.
So lets recap what we have done in this post: In case it is correct that this universe is 13.8 billion years old, in that case the math professors have found only three versions of the fundamental theorem of calculus. They have two slightly different versions for the real line and one for the complex plane. So basically they only have two Fundamental Theorems of Calculus. In this post we looked at the n-dimensional real spaces equipped with either the complex or the circular multiplication. So for every fixed dimension n there are two fundamental theorems related to those two multiplications. As such in this post we found an infinite number of fundamental theorems so although I don’t like it to write general theory, all in all this was not a bad day at the office.
So for the time being included this post General Theory Part 4 on integration, for the time being, this is all general theory that there is. It contains the ancient quest for a number who’s square equals minus one. The matrix big E is handy if you want to study all kinds of multiplications while part 3 and 4 cover differentiation and integration.
This post is basically a video about the so called Einstein de Haas effect from the Action Lab (a video channel). This experiment is often mentioned as experimental validation that electrons have so called “Intrinsic angular momentum”. The experimental setup is very easy to explain, look in the next picture:
A metal cylinder is hanging from a wire (the guy in the video uses tooth floss because that has no winding twist in it so the cylinder will not rotate). If placed in a vertical magnetic field or such a vertical magnetic field is flipped on, the cylinder rotates a little bit. Often in the experimental setup a coil magnet is used, but it can be any more or less perfect vertical magnetic field. The effect of the rotation is rather small so in video’s like this you often see some shiny or reflecting metal glued to the cylinder and with a light the rotation is amplified for us to see.
This is all there is; a relatively simple experimental setup.
The explanation you always see is that the unpaired electrons in the metal cylinder align themselves with the applied magnetic field. So that’s the logic for the explanation of this experiment.
How different is it for the Stern Gerlach experiment that is very similar because it is about the behavior of unpaired electrons in a vertical applied magnetic field. In the SG experiment the beam of silver atoms is split in two and now the logic is as next, quote:
This means that when you take a beam of electrons whose angular momenta are all randomly oriented, if you measure the z component of angular momentum you get one of only two different values.
But if your explanation in the Einstein de Haas effect would be this 50/50 percent probability in spin up or spin down, that would imply zero rotation and therefore once more day the physics professors will talk out of their necks and now it must be logical that all electrons align. Source of my above quote: Measuring Electron Spin- the Stern-Gerlach Experiment
Furthermore it is a fundamental basis of quantum computing that it must be possible to have superpositions of quantum states. So if the explanation of the Einstein de Haas effect would be correct, there is no randomness in electron spin measurements via application of external magnetic fields. You just can’t eat it from both sides: either all electrons will do the same or the probabilistic nature of quantum mechanics is true. Anyway here is the video with the title: Do Electrons Really Have “Intrinsic” Angular Momentum?
https://www.youtube.com/watch?v=uQ5w4_0S2l4
That was it for this post on magnetism in particular the very different explanations you hear when we are talking about the same thing: The reaction of an electron on a vertical magnetic field.
Some time after I started writing this post I thought “Hey why not look up what is more or less offically said on this theorem in the internet”. So I did and found out there are three versions of this theorem that basically says you can do integration with a primitive. That was a tiny surprise to me because the way I remembered it was there is just only one. There are two versions on the real line and one for the complex plane. The first real line version says that the integral of a function on the real line equals the difference that the primitive has in the begin and endpoint of integration. The second real line version uses a variable in the endpoint of integration, say x, and define a primitive F(x) of a function f(x) as such. After that it must be shown that the derivative F'(x) = f(x). And the third version says you can do line integration (or integration along a curve traditionally named gamma) also using a primitive but now you must take into account the way differentiation works in the complex plane.
So there is not one such fundamental theorem but the official theory says it’s three. Now why three? Very simple: The professional math people know of no other spaces where you can do integration with a primitive. I’ve said it before and repeat it once more: The 4D quaternions are nice things but when it comes to differentiation and integration it is hard to get a bigger mess of total gibberish. That’s why the professional math professors don’t have such a fundamental theorem for the quaternions.
But for the 3D complex numbers that are the main topic of this website, it can also be done. But hey this is now the year 2025 and this website is almost 10 years old and on top of that I found the 3D complex numbers back in the year 1990, so why only now this theorem in the year 2025? Now over the years I have always used this kind of integration when I needed it. For example the number tau for the 3D complex numbers was calculated the first time by using integration while I developed the matrix diagonalization methods only later to deal with the problems you get in say five or seven dimensional complex numbers. For people who don’t have it clear what the numbers tau are: They are the logarithm of an imaginary unit. For example the log of the imaginary unit i on the complex plane is i times pi/2 as was already found by the good old Euler. Now for the 3D complex numbers it’s a bit more difficult but you can find such log’s of imaginary numbers indeed with integrating just the inverse.
But I always thought there would be some kind of trouble if you integrate just inside the subspaces of non-invertible numbers. So that’s more or less why I never ever formulated such a fundamental theorem in all those years. I only used integration when I needed it and that was it.
To my excuse there are indeed some subtilities, I once tried to find the primitive of say e^X and yes, no problemo, it is just e^X. While if you calculate the integral now with a 3D number X but multiply it by that famous number alpha, the primitive changes in a dramatic fashion. So all those years I thought that even for say the exponential function there was not just one primitive to do all the work. Yet now I take a deeper look into it, this was all a bit stupid of me. So it’s a lame excuse but compared to the professional math professors who can’t even find the complex 3D numbers, I shine as the stable genius I am… Ahum, this post is only 9 pictures long and has 3 additional figures and one video about the fundamental theorem on the real line. So all in all there are 12 pictures and 1 video below.
Lets get this party started:
The next picture is the so called Figure 1 picture and it shows where the determinant is one. So on the red colored graph you can do the ‘divide by beta’ thing in the limit for the derivative of a function. The problems with taking such a limit on the space where det(X) = 0, you can’t divide by such a beta so doesn’t that cause some problems? Well no, you can always flip hin und her between the two above definitions of taking a derivative.
Figure 1: I am not crazy: Can’t divide by beta? Well, try a multiplication by beta…
And here is the so called Figure 2 picture where I depicted a line segment inside the main plane of non-invertible numbers in the 3D complex numbers. Therefore I invite you to think a bit along those lines, does it matter if they are inside or outside the space of det(X) = 0?
I have a link for you to a page from the website from Stephen Wolfram where the three fundamental theorems of calculus are explained. Fundamental Theorems of Calculus Now I published the above about 24 hours ago but I was forgotten to place the link to Wolfram. And today I was watching youtube and to my surprise a video from Hannah Fry came floating along while it said it was about the fundamental theorem of calculus. It’s all very very basic because Hannah uses it also to craft an introduction to integration using the limit of an elementary Riemann sum. For most readers it is a bit too simple I guess but in case you harldy know what integration is, for those it is a very good video.
And for no reason at all I also made a cube with her face on it. We all love Hannah because she is relatively good at popularizing math. And that’s a good thing because it makes the general population a bit less stupid. Anyway that is what you might hope for but don’t let you hope become to big because the human brain and math is often not a good combination. We’re just a fucking stupid monkey species, ok we are the smartest monkeys around but we’re still a monkey species…
This is the end of this post, now we have a fourth so called Fundamental theorem of calculus. Lets leave it with that.
