A few posts back I used the number 210 to craft seven so called ‘primitive’ counter examples to the famous last theorem of Fermat. Each of those seven primitives can be changed in an infinite number of ways so we have seven streams of counter examples to the last Fermat theorem. It has to be remarked that all counter examples I found since Jan are all based on the so called divisors of zero idea. So if you hear people talking about that in a timespan of 3.5 centuries nobody was able to find counter examples, they are not lying if they mean a counter example on the space of real integers. Yet in Jan this year we observed I had two counter examples using the 3D Gaussian integers, it was one or two days later I found all those counter examples on the spaces of modulo arithmetic.
Beside his so called last theorem Fermat has done a lot more and one of those things is Fermat’s little theorem. To my surprise there are many more variants possible of this little theorem. The little theorem says that for a number a coprime to some prime number p the following holds:
a^p = a mod p. Two numbers are coprime if they share no common factor, if a is a number between 1 and p this is always the case.
The most simple example: a = 2 and p = 3. The little theorem now says that 2^3 mod 3 = 2. This is correct because the remainder of 8 divided by 3 equals 2.
The variants I found can be summarized as next:
2^3 mod 6 = 2 and
3^2 mod 6 = 3.
As you see I take it modulo a composite number. I still do not have a satisfactory proof so for the time being this is a conjecture. I am planning a seperate post for outlining where in my view the problems are that must be proved for the status of conjecture being dropped. So for the time being this is Reinko’s little conjecture.
But can you use a composite number with more than two factors? Yes but you can only use prime numbers in the exponent. Not that it will always fail if you do not use a prime exponent but that is a mathematical story for another day. Anyway this post uses the number 210 because it is the smallest number with four prime factors.
Before we go to the content of this post, to my surprise yesterday I observed a proof that is strikinly similar to the easy way I constructed those counter examples to the last theorem of Fermat. I found it on brilliant.org, here is a link:
https://brilliant.org/wiki/fermats-little-theorem/
Over there they prove the little theorem for a + 1 if it is true for a. Now why do they not use it for finding counter examples to the last theorem of Fermat? Well my dear reader, the human mind is bad at math. We are only monkeys or smart apes if you want, math is something that fascinates our minds but humans are horribly bad at math. Believe me: I am a human myself…;)
Here is a picture from that proof from brilliant dot org:
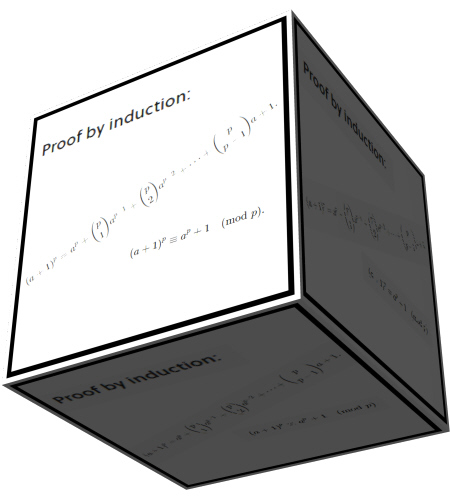
Therefore they vanish when you take the modulo p thing.
The whole post is only two pictures long, each of the ususal size of 550×775 pixels. Here we go:


Ok, that was it for this post. Thanks for your attention & see you in the next post.