To my amazement there are many more forms of the so called Fermat little theorem. Fermat’s little theorem uses numbers that are relatively prime to each other (also known as coprime numbers or better: coprime real integers). I hope it is not confusing for you that I write ‘real integers’ but that is meant to make clear these are not Gaussian integers but integers from the real line.
The little theorem of Fermat has some generalizations like the Euler theorem and a person named Carmichael also worked on stuff like that. Yet the coprime stuff is always assumed while the results I found last week do not need that at all. But I do need prime numbers in the exponent, that’s all.
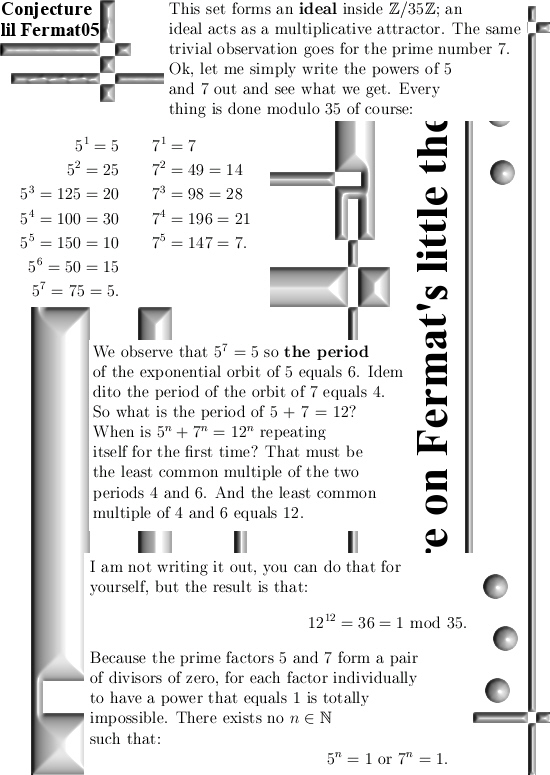
When I found those counter examples to Fermat’s last theorem about 3 months back I was amazed I could find nothing of that on the entire internet. Ok my first stuff was done with 3D complex & circular Gaussian integers so that is logical nobody else writes about that. But that expressions like 5^n + 7^n = 12^n modulo 35 is something that baffled my mind. This is so simple to prove that it is hard to understand why this is not a standard counter example to the last theorem of Fermat. To refresh your mind: the last theorem of Fermat says there exists no integers such that x^n + y^n = z^n for n > 2. This has been an open problem for about 3.5 centuries of time, it was solved by Andrew Wiles in the beginning of the nineties of the last century but even Andrew never mentions those easy to craft counter examples to the last theorem of Fermat.
A paradox.
The last theorem of Fermat was unproven for centuries. But the far more easy little theorem of Fermat was proven rather quick and that proof is very easy compared to the Andrew Wiles thing. Now I am having the opposite problem: The counter examples to Fermat’s last theorem are so simple to construct that in the beginning I was hesitant to use it all. While for these new variants of the little theorem of Fermat, I do not know how to prove that. So my stuff is more or less opposite to the historical developments as they are known; that is why I consider this a little paradox.
In this post I formulate a few easy to understand variants of the little theorem of Fermat. In this post I choose to do it as symmetrical as possible like in the next pair:
7^11 = 7 modulo 77 &
11^7 = 11 modulo 77.
As you see on inspection; these are clearly variants of the little theorem but the exponents and the 77 of the modulo thing are not coprime. For myself speaking I consider the above pair as an example of ‘mathematical beauty’. Of course it is hard to give a definition of ‘math beauty’, you recognize it when you see it but it is hard to define because beauty itself is not a mathematical object or so.
Anyway beautiful or ugly as a math professor, this post is six pictures long all in the standard format of 550×775 pixels. Here we go with the picture stuff:





A few posts back I crafted seven counter examples to the last theorem of Fermat and those were based on the number 210. Actually each of those seven ‘primitives’ gave rise to an infinite series of counter examples so that the overpaid math professors once more know their contribution to this all: ZERO!
But you can make four new little Fermat theorems using the number 210 so may be that is the next post. On the other hand the USA based Fermilab has all kinds of new results out upon the muon and they keep on thinking that elementary particles like electrons and muons are magnetic dipoles. Instead of offering some fundamental proof for the magnetic dipole nature of electrons we only get a complicated story that, as usual, neglects that electrons and muons get accelerated by magnetic fields.
So I don’t know about the next post. Well thanks for your attention, have a healthy life and ruthlessly kill all math professors. Or may be not…;)