Post number 191 already so it will be relatively easy to make it to post number 200 this year. If you think about it, the last 190 posts together form a nice bunch of mathematics.
In this post we will pick on where we left it in the last post; we start with the three dimensional complex and circular numbers. In the introduction I explain how the stuff with a pair of divisors of zero works and from there it is plain sailing so to say. When back in Jan of this year I constructed the first counter example to the last theorem of Pierre de Fermat I considered it a bit ‘non math’ because it was so easy. And when one or two days later I made the first counter example using modular arithmetic I was really hesitant to post it because it was all so utterly simple…
But now half a year later it has dawned on me that all those professional math professors live up to their reputation of being overpaid under performers because in a half year of time I could find not one counter example on our beloved internet. And when these people write down some calculations that could serve as a counter example, they never say so and use it only for other purposes like proving the little theorem of Fermat. It has to be remarked however that in the past three centuries of time, when people tried to find counter examples, they likely started with the usual integers from the real line and as such tried to find counter examples. Of course that failed and this is not because they are stupid or so. It is the lack of number spaces they understand or know about that prevented them in finding counter examples to the last theorem of Pierre de Fermat.
If you do not know anything about 3D complex or circular numbers, you are not a stupid person if you cannot find counter examples to the last theorem. But you are definitely very very stupid if you do not want to study 3D complex numbers, if you refuse that it proves you have limited mathematical insights and as such likely all your other math works will be limited in long term value too.
While writing this post all of a sudden I realized I skipped at least one space where counter examples are to be found: It is on the space of so called split complex numbers. I did not invent that space, that was done by the math professors. The split complex numbers are a 2D structure just like the complex plane but instead of i^2 = -1, on the split complex plane the multiplication is ruled by i^2 = 1. Likely I will write a small post about the split complex number space. (Of course in terms of the language of this website, the 2D split complex numbers are the 2D circular numbers.)

This post is 8 pictures long, I kept on to number them according to the previous post so we start at picture number 11. They are all in the size of 825×550 pixels. I hope it is worth of your time. Here we go:

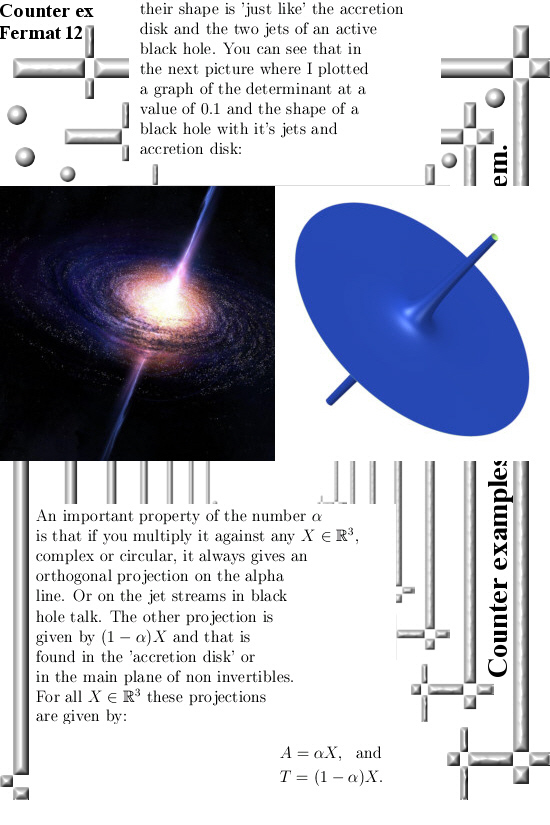
In this post I used only ‘my own spaces’ like 3D complex and circular numbers and the 4D complex numbers. As such it will be 100% sure the math professionals will 100% not react on it. Even after 30 years these incompetents are not able to judge if there is any mathematical value in spaces like that. Why do we fork out so much tax payer money to those weirdo’s? After all it is a whole lot of tax payer money for a return of almost nothing. Ok ok a lot of math professors also give lectures in math to other studies like physics so not all tax payer money is 100% wasted but all in all the math professors are a bunch of non-performers.

I think I will write a small post about the 2D split complex numbers because that is a space discovered by the math pro’s. So for them we will have as counter examples to the last theorem of Pierre de Fermat all that modulo calculus together with the future post on the split complex numbers. Not that this will give a reaction from the math pro’s but it will make clear you just cannot blame me for the non reactive nature of the incompetents; the blame should go to those who deserve it… Or not?

May be the next post is about magnetism and only after that I will post the split complex number details. We’ll see, anyway if you made it untill here thanks for your attention and I hope you learned a bit from the counter examples to the last theorem of Pierre de Fermat.