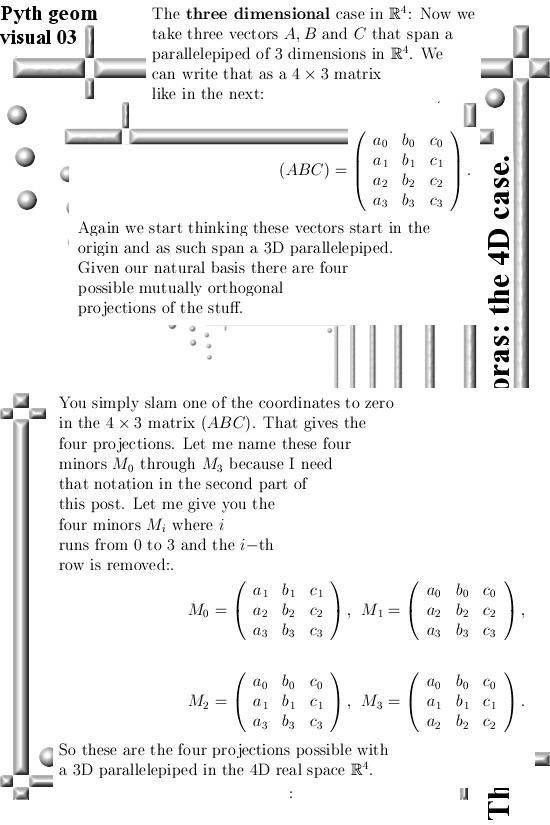
A few posts back I showed you that pdf written by Charles Frohman where he shows a bit of the diverse variants of the more general theorem of Pythagoras there is. At school you mostly learn only about the theorem for a triangle or a line segment and it never goes to anything else. But there is so much more, in the second half of this post I show you three vectors in 4D space that span a parallelepiped that is three dimensional. From the volume of such a thing you can also craft some form of Pythagorean theorem; that paralellepiped can be projected in four different ways and the squares of the four volumes you get equals the square of the original parallelepiped.
I would like to remark I hate that word ‘paralellepiped’, if you like me often work without any spell correction this is always a horrible word…;)

Now my son came just walking by, he reads the title of my post and he remarks: It sounds so negative or sarcastic this ‘full theorem’. And no no no I absolutely do not mean this in any form of negative way. On the contrary I reconmend you should at least download Charles his pdf because after all, it was better compared to what I wrote on the Pythagoras subject about 10 years ago.

But back to this post: What Charles names the full theorem of Pythagoras is likely that difficult looking matrix expression and from the outside it looks like you are in a complicated space if you want to prove that thing. The key observation is that all those minor matrices are actually projections of that n x k matrix you started with. So that is what the first part of this post is about.

The second part is about a weird thing I have heard more than once during my long lost student years: Outside the outer product of two vectors we have nothing in say 4D space that gives a vector perpendicular to what you started with. I always assumed they were joking because it is rather logical that if you want a unique one-dimensional normal vector in say 4D space, you must have a 3D dimensional thing to start with. That is what we will do in the second part: Given a triple of vectors (ABC) in four dimensional space, we construct a normal vector M to it. With this normal vector, after normalization of course, it gives now a handy way to calculate the volume of any of those paralellepiped things that hang out there.

Ok, lets go: Six pictures long but easily readable I hope.

All that is left is trying to find back that link to Charles his pdf.

That was it for this post. I hope you liked it, I surely liked the way you can calculate those paralellapipidedted kind of things. Thx for your attention and see you in the next post.