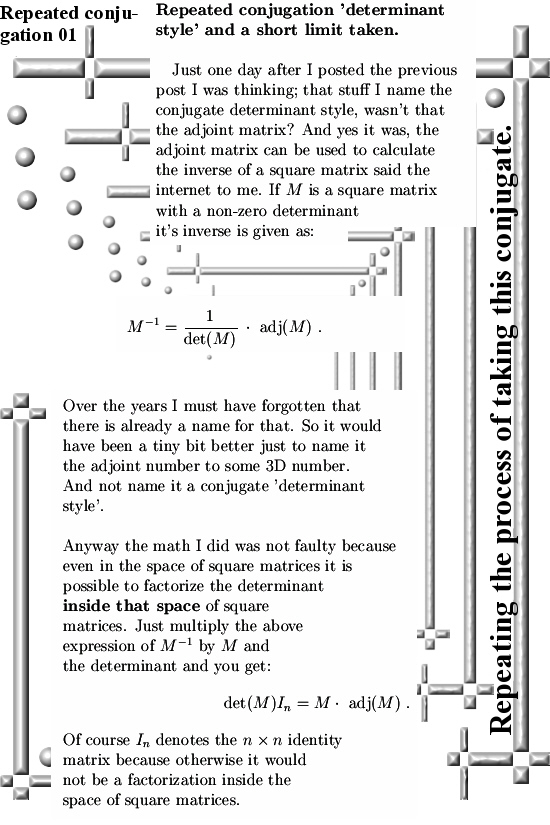
This post is easy going for most people who have mastered the art of finding the inverse of a square matrix using the so called adjoint matrix. I was curious what happens to a 3D circular number if you take the conjugate ‘determinant style’ twice. In terms of standard linear algebra this is the same as taking the adjoint of the adjoint of a square matrix.
It is well known by now (I hope anyway) that 3D complex and circular numbers contain a set of numbers with a determinant of zero, you can’t find an inverse for them. To be precise, if you take some circular 3D number, say X, and you make some limit where you send X into a not invertible number, you know the inverse will blow up to infinity.
But the conjugate ‘determinant style’ does not blow up, on the contrary in the previous post we observed that taking this kind of conjugate gave an extra zero eigenvalue in this conjugate.
In terms of linear algebra: If a square matrix is not invertible, it’s adjoint is ‘even more’ non invertible because a lot of the eigenvalues of that matrix turn to zero.
And although the inverse blows up to infinity, the cute result found is that it blows up in a very specific direction. After all it is the fact that the determinant goes to zero that blows the whole thing up, the conjugate ‘determinant style’ is as continuous as can be around zero…
It’s a miracle but the math is not that hard this time.
Four pictures for now and I plan on a small one picture addendum later.
So lets go:



All in all this is not a deep math post but it was fun to look at anyway. May be a small appendix will be added later, so may be till updates inside this post or otherwise in some new post.
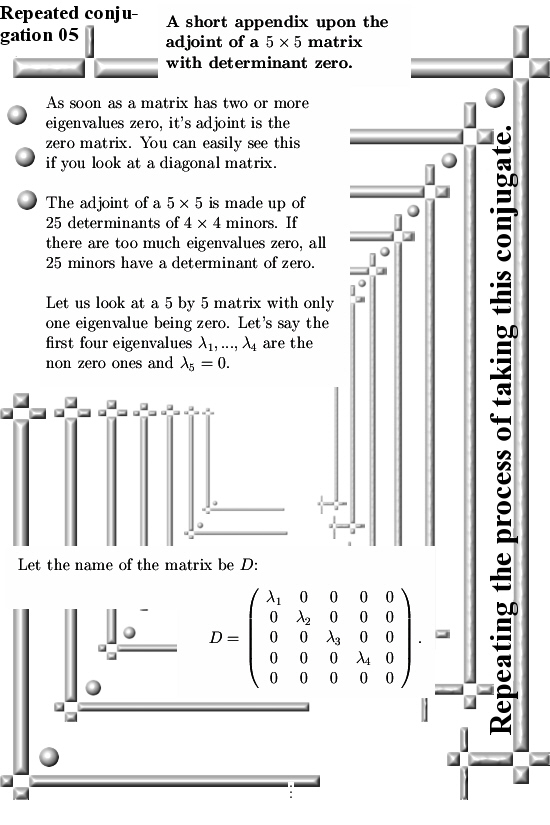
Added Sunday 16 April: A small appendix where you can see what the adjoint taking process is doing with the eigenvalues of a 5×5 diagonal matrix. The appendix was just over one picture long so I had to spread it out over two pictures. You understand fast what the point is if you calculate a few of the determinants of those minor matrices. Remark here with a 5×5 matrix all such minors are 4×4 matrices so it is the standard setting and not like that advanced theorem of Pythagoras stuff.
Well it all speaks for itself:
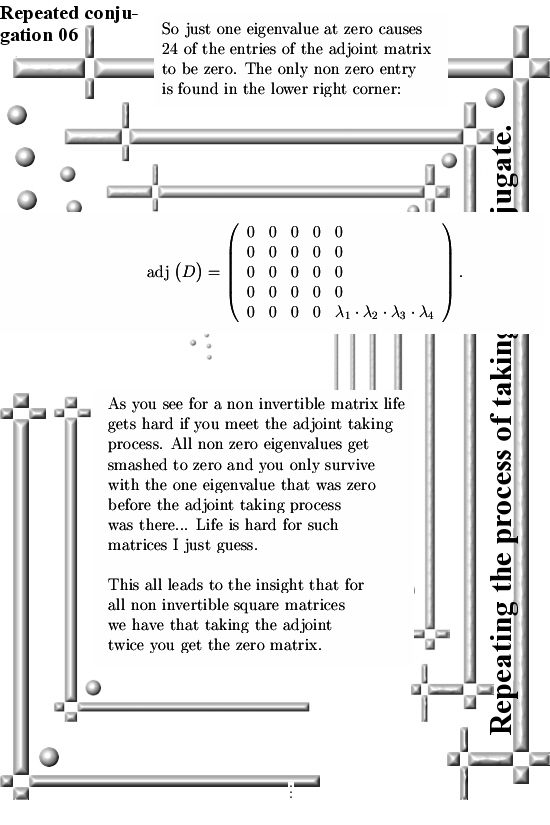
Ok, that was it for this update. Thanks for the attention and see you in another post.