Category Archives: Exponential curves

Comparison of the conjugate on five different spaces.

2D multiplications, 3D complex numbers, Exponential circle, Exponential curves, Matrix representation

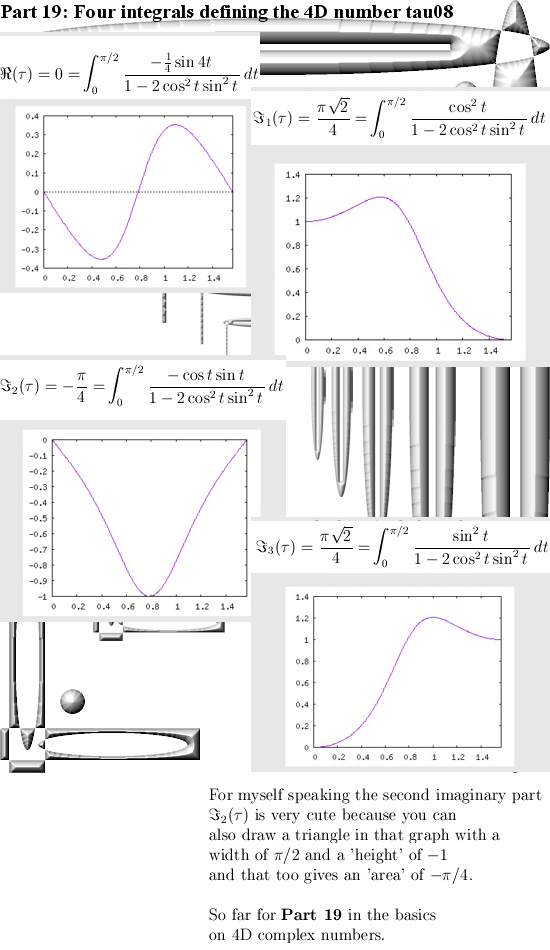
To be a bit precise: I think two spaces are different if they have a different form of multiplication defined on them. Now everybody knows the conjugate, you have some complex number z = x + iy and the conjugate is given by z = x – iy. As such it is very simple to understand; real numbers stay the same under conjugation and if a complex numbers has an imaginary component, that gets flipped in the real axis.

But a long long time ago when I tried to find the conjugate for 3D complex numbers, this simple flip does not work. You only get advanced gibberish so I took a good deep look at it. And I found that the matrix representation of some complex z = x + iy number has an upper row that you can view as the conjugate. So I tried the upper row of my matrices for the 3D complex and circular numbers and voila instead of gibberish for the very first time I found what I at present day name the “Sphere-cone equation”.

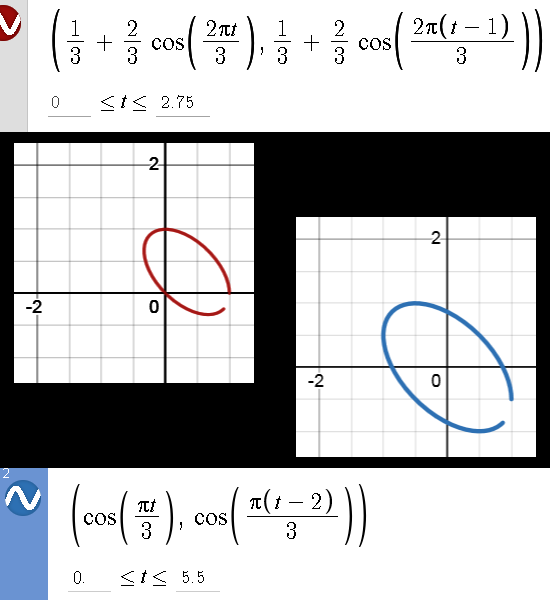
I never gave it much thought anymore because it looked like problem solved and this works forever. But a couple of months ago when I discovered those elliptic and hyperbolic versions of 2D numbers, my solution of taking the upper row does not work. It does not work in the sense it produces gibberish so once more I had to find out why I was so utterly stupid one more time. At first I wanted to explain it via exponential curves or as we have them for 2D and 3D complex numbers: a circle that is the complex exponential. And of course what you want in you have some parametrization of that circle, taking the conjugate makes stuff run back in time. Take for example e^it in the standard complex plane where the multiplication is ruled by i^2 = -1. Of course you want the conjugate of
e^it to be e^-it or time running backwards.

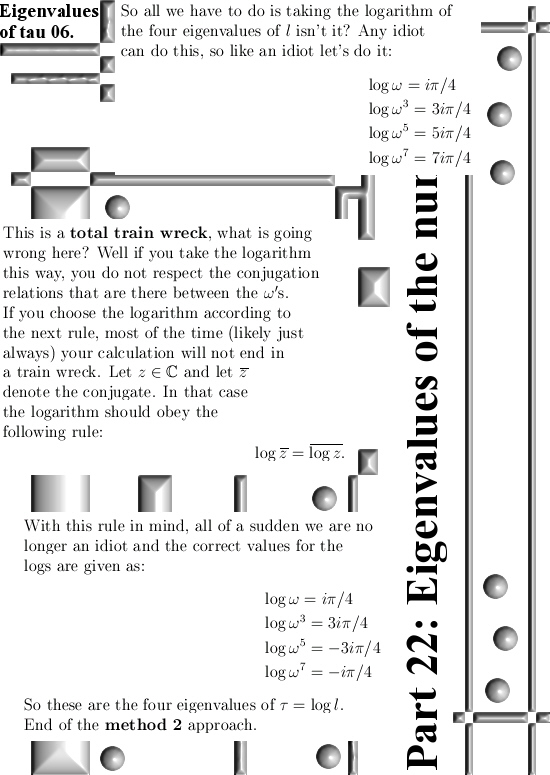
But after that it dawned on me there is a more simple explanation that at the same time covers the explanation with complex exponentials (or exponential circles as I name them in low dimensions n = 2, 3). And that more simple thing is that taking the conjugate of any imaginary unit always gives you the inverse of that imaginary unit.

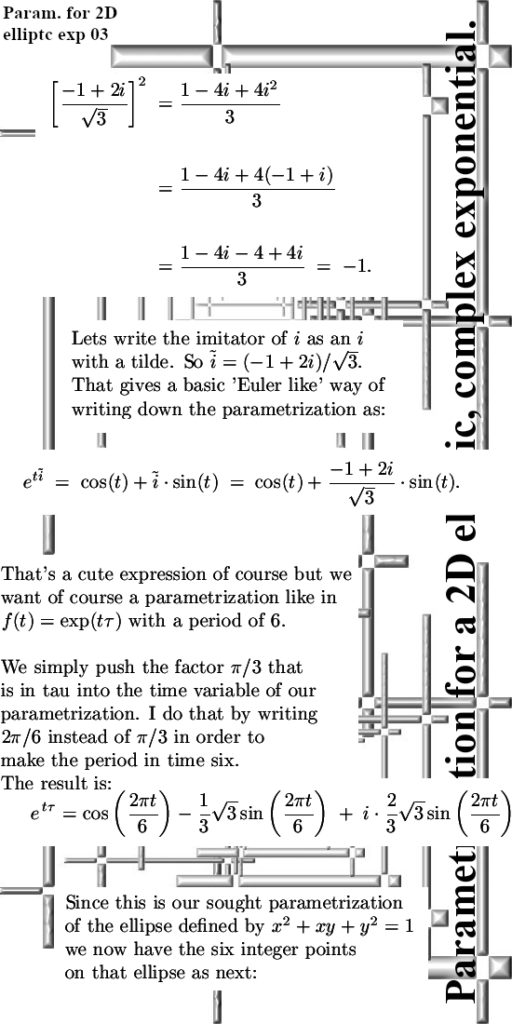
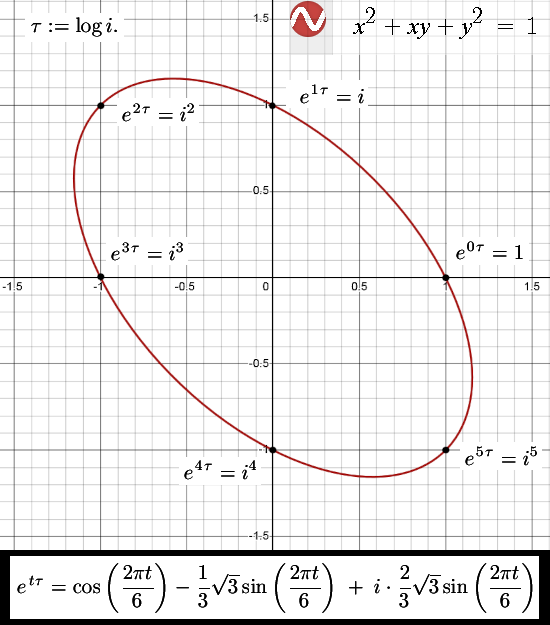
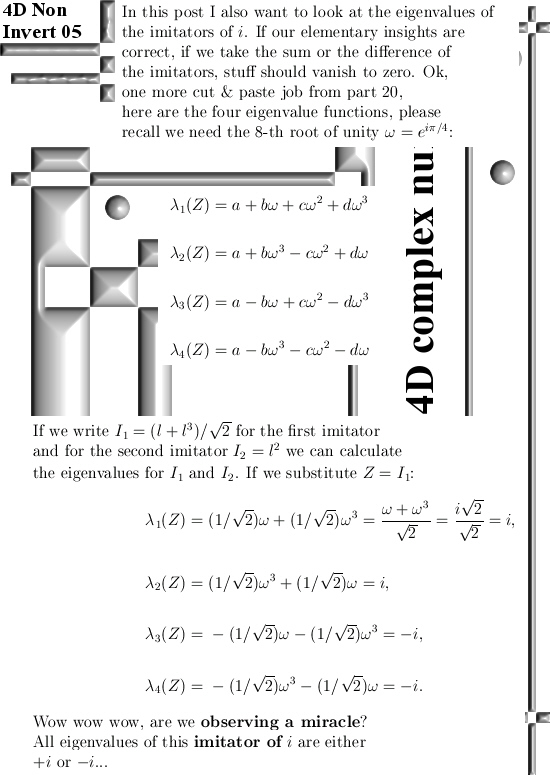
And finding the inverse of imaginary units in low dimensions like 2D or 3D complex numbers is very simple. An important reason as why I look into those elliptic complex 2D numbers lately is the cute fact that if you use the multiplication rule i^2 = -1 + i, in that case the third power is minus one: i^3 = -1. And you do not have to be a genius to find out that the inverse of this imaginary unit i is given by -i^2 .
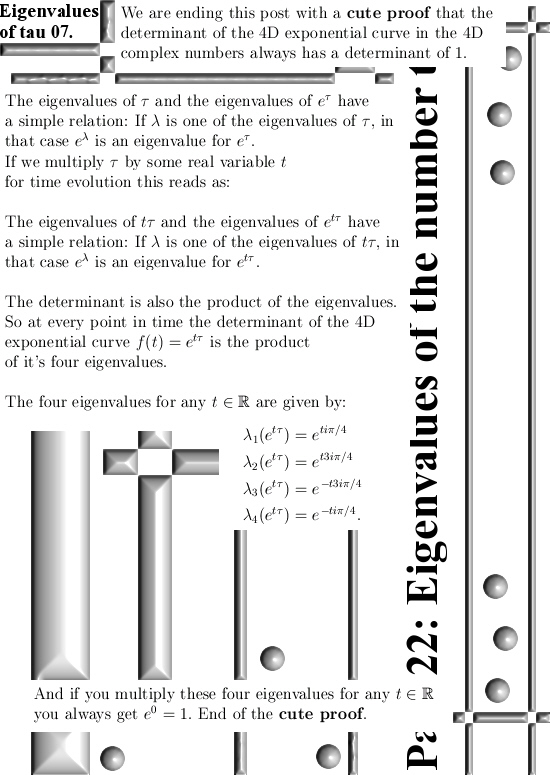
If you use the idea of the conjugate is the inverse of imaginary units on those elliptic and hyperbolic version of the complex plane, if you multiply z against it’s conjugate you always get the determinant of the matrix representation.
For me this is a small but significant win over the professional math professors who like a broken vinyl record keep on barking out: “The norm of the product is the product of the norms”. Well no no overpaid weirdo’s, it’s always determinants. And because the determinant on the oridinary complex plane is given as x^2 + y^2, that is why the math professors bark their product norm song out for so long.

Anyway because I found this easy way of explaining I was able to cram in five different spaces in just seven images. Now for me it is very easy to jump in my mind from one space to the other but if you are a victim of the evil math professors you only know about the complex plane and may be some quaternion stuff but for the rest you mind is empty. That could cause you having a bit of trouble of jumping between spaces yourself because say 3D circular numbers are not something on the forefront of your brain tissue, in that case only look at what you understand and build upon that.

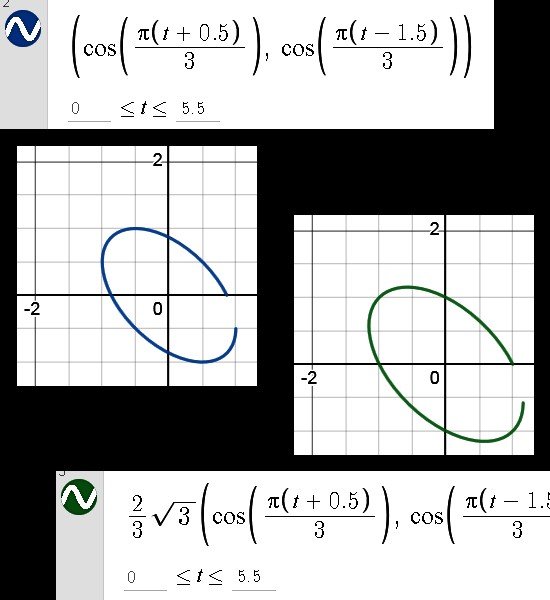
All that’s left for me to do is to hang in the seven images that make up the math kernel of this post. I made them a tiny bit higher this time, the sizes are 550×1250. A graph of the hyperbolic version of the complex exponential can be found at the seventh image. Have fun reading it and let me hope that you, just like me, have learned a bit from this conjugate stuff.
The picture text already starts wrong: It’s five spaces, not four…

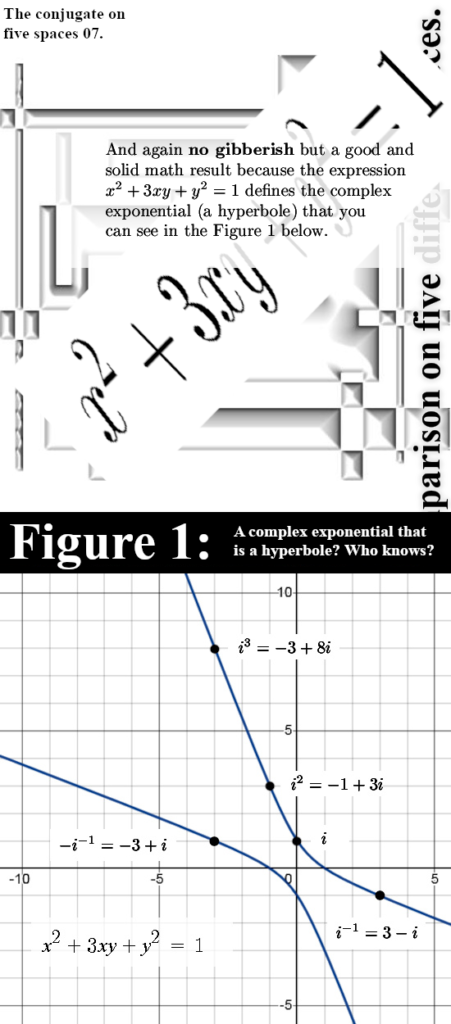
At last I want to remark that the 2D hyperbolic complex numbers are beautiful to see. But why should that be a complex exponential while the split complex numbers from the overpaid math professors does not have a complex exponential?
Well that is because the determinant of the imaginary unit must be +1 and not -1 like we have for those split complex numbers from the overpaid math professors. Lets leave it with that and may I thank you for your attention if you are still awake by now.

Two parametrizations for the ‘unit’ ellipse in the i^2 = -1 + i kind of multiplication.

2D multiplications, 3D complex numbers, Exponential circle, Exponential curves

Basically this post is just two parametrizations of an ellipse, so all in all it should be a total cakewalk… So I don’t know why it took me so long to write it, ok ok there are more hobbies as math competing for my time. But all in all for the level of difficulty it took more time as estimated before.
In the last post we looked at the number tau that is the logarithm for the imaginary unit i and as such I felt obliged to at least base one of the parametrizations on that. So that will be the first parametrization shown in this post.
The second one is a projection of the 3D complex exponential on the xy-plane. So I just left the z-coordinate out and see what kind of ellipse you get when you project the 3D exponential circle on the 2D plane. Acually I did it with the 3D circular multiplication but that makes no difference only the cosines are now more easy to work with. Anyway the surprise was that I got the same ellipse back, so there is clearly a more deeper lying connection between these two spaces (the 3D circular numbers and these 2D complex multiplication defined by i^2 = -1 + i).
A part of the story as why there is a connection between these spaces is of course found into looking at their eigenvalues. And they are the same although 3D complex numbers have of course 3 eigenvalues while the 2D numbers have two eigen values. A lot of people have never done the calculation but the complex plane has all kinds of complex numbers z that each have eigenvalues too…
Anyway I felt that out of this post otherwise it would just become too long to read because all in all it’s now already 10 images. Seven images with math made with LaTex and three additional figures with sceenshots from the DESMOS graphical package.
By the way it has nothing to do with this post but lately I did see a video where a guy claimed he calculated a lot of the Riemann zeta function zero’s with DESMOS. I was like WTF but it is indeed possible, you can only make a finite approximation and the guy used the first 200 terms of the Riemann zeta thing.
At this point in time I have no idea what the next post will be about, may be it’s time for a new magnetism post or whatever what. We’ll wait and see, there will always pop something up because otherwise this would not be post number 254 or so.
Well here is the stuff, I hope you like it or enjoy it.

Figure 1: This parametrization is based on the number tau.
Figure 2: The projection in red, stuff without 1/3 and 2/3 in blue.
Figure 3: The end should read (t – 1.5) but I was to lazy to repair it.

That was it for this post, of course one of the reasons to write is that I could now file it under the two categories “3D complex numbers” and “2D multiplications” because we now have some connection going on here.
And I also need some more posts related to 3D complex numbers because some time ago I found out that the total number of posts on magnetism would exceed those of the 3D complex numbers.

And we can’t have that of course, the goal of starting this website was to promote 3D complex numbers via offering all kinds of insights of how to look at them. The math professors had a big failure on that because about 150 years since Hamilton they shout that they can’t find the 3D complex numbers. Ok ok, they also want it as a field where any non-zero number is invertible and that shows they just don’t know what they are talking about.
The 3D complex numbers are interesting simply because they have all those non-invertible numbers in them.

It is time to split my dear reader so we can both go our own way so I want to thank you for your attention.

Part 22: The eigenvalues of the 4D complex number tau.

4D complex numbers, Exponential circle, Exponential curves, Matrix representation

This post took me a long time to write, not that it was so very difficult or so but lately I am learning that graphics program named GIMP. And that absorbs a lot of time and because I am only sitting behind my computer a few hours a day, doing GIMP goes at the expense of writing math…

I always make my pictures with an old graphics program named Picture Publisher 10. It is so old that on most windows 7 and windows 10 it does not run but it has all kinds of features that even the modern expensive graphics programs simply still don’t have. Silently I was hoping that I could use GIMP for my math texts and yes that could be done but in that case I have to use old background pictures forever. Or I have to craft a ‘new style’ for making the background in the math pictures that can last at least one decade.

But let’s not nag at what GIMP cannot do, if you install just one large addon you have about 500 filters extra and my old program PP10 comes from an era when the word ‘addon’ was not a word used ever. Before we jump to the math, let me show you a nice picture you can make with the tiling filter inside GIMP. It is about my total bicycle distance since I bought this bicycle computer, it says 77 thousand km so the Tour the France racers can suck a tip on that:

Just one tile already looks nice.
And this is how four of these tiles look.

Ok, let us look at the math of this post. This is part 22 in the introduction to the 4D complex numbers. The 4D complex numbers have three imaginary units, l, l^2 and l^3. And the stuff that makes it ‘complex’ is the fact that l^4 = -1, you can compare that to the complex plane where the square of the imaginary unit equals -1.

On the complex plane, if you know what the logarithm of i is, you can use that to find the exponential circle also known as the complex exponential. This is what the number tau always is in all kinds of spaces: It is always the logarithm of the first imaginary unit that has a determinant of +1. In this post we will calculate the eigenvalues of this important number tau. That will be done with two methods. In the first method we simply use the eigenvalue functions, plug in the number tau and voila: out come the four eigenvalues. In the second method we first calculate the four eigenvalues of the imaginary unit l and ‘simply’ take the logarithm of those four eigenvalues.

It is not much of a secret that my style of work is rather sloppy, I never order my work in theorems, lemma’s or corrolaries. It is not only that such an approach if too much a straight jacket for me, it also frees me from a lot of planning. I simply take some subject, like in this case the eigenvalues of the number tau and start working on explaining that. While writing that out there always comes more stuff around that I could include yes or no. In this post what came around was that only after writing down the four eigenvalues I realized that you can use them to prove that the exponential curve (the 4D complex exponential) has a determinant of 1 for all points on that curve. That was an important result or an important idea so I included it because that makes proving that the determinant is 1 much more easy.

Now a few posts back with that video from that German physics guy Alexander Unzicker I said that he (and of course all other physics professionals) could always use the 4D complex exponential curve for the ‘phase shifts’ that those physics people always do. But for doing such 4D ‘phase shifts’ or unitary transformations in general, you need of course some kind of proof that determinant values are always +1. Well Alexander, likely you will never read this post but below you can find that very proof.

The previous post was from the end of August and now I think about it: Have I done so little math during the last four weeks? Yes there were no results simply left out, it was only penning down these eigenvalues of tau and the idea you can use these eigenvalues for proving the 4D exponential curve always has a determinant of 1. It is amazing that GIMP can hinder the creation of fresh math… 😉

The math pictures are seven in number, all in the usual size of 550×775 pixels. I hope you like it and see you in the next post.

So these are the four eigenvalues of the number tau and based on that the four eigenvalues of the 4D complex exponential for a values of time.

That’s it for this post. See you in a future post.

Added on 27 Sept 2020: This proceeds the two pictures made with GIMP that started this post. I just made the whole stuff on a cube (actually it is a beam because the starting picture is not a square). It is amazing how good such filters in GIMP are:

That does not look bad at all!

Ok, you are now at the real ending of this post.

Part 21: More on the structue of non-invertible 4D complex numbers.

4D complex numbers, Exponential curves

Finally I have some time left to update this website. I would like to proceed with another part into the introduction to the four dimensional complex numbers. The previous part 20 dates back to 02 Feb 2019 and that too was about this structure of the non-invertible numbers in four dimensional complex space.

When I was reading back a few of my own old writings like part 20 from 02 Feb it struck me that those non-invertible numbers are all just linear combinations of the so called imitators of i. Imitators of i live always in dimensions higher than 2 and they mimic the behaviour of the number i from the complex plane. For example in the spaces of the 3D complex and circular numbers those imitators are not capable of squaring to minus one but they do a pretty good job at rotating stuff by 90 degrees if you multiply by them. In the 4D complex space there are two of such imitators and they do square up to minus one. Of course this is related to the fact you can find two copies of the 2D complex plane in the 4D complex space. So in that regard the 4D complex numbers are a bit different compared to the 4D quaternions that exist of 3 copies of the complex plane (but those do not commute and as such you cannot differentiate or integrate stuff).

Another interesting detail is that in the 4D complex number system the set on non-invertible numbers consists of just two lines that are perpendicular to each other. That is very different from the 3D situation where the set of non-invertibles is always a plane combined with a perpendicular line through zero. The reason that in 4D complex space the set is so small lies of course in the matrix representation and the determinant. On the 4D complex space the determinant is non-negative, just like the determinant is non-negative on the complex plane. Every 4D complex number has four eigenvalues and they come in conjugate pairs, so the product of these four eigenvalues gives the determinant hence the determinant cannot be a negative real number.

And say for yourself: aren’t the eigenvalue functions a very handy thing? If you want to find the eigenvalues of let’s say the 4D complex number Z = 1 + 2l + 3l^2 + 4l^3, that is often a horrible mathematical exercise. But once you have these four eigenvalue functions, you simply plug in any Z and voila: there are your 4 eigenvalues.
This post is seven pictures long, as usual in the 550×775 pixel size.

Remark det(Z) = 0 does not show up in a ray tracing method.
Oops, did I forget the eigenvalues of the number tau?

Ok, that was it for this post. Till updates my dear reader.

The 4D Dirichlet kernel related to the 4D Fourier series.

3D complex numbers, 4D complex numbers, Exponential curves

Is the glass half full or half empty? You can argue that it is half full because the so called ‘pure tones’ as introduced in the previous post work perfectly for making a four dimensional Fourier series based on the 4D complex numbers. The glass is half empty because I started this Fourier stuff more or less in order to get some real world applications done, but 1 dimensional signals like a sound fragment do not reconstruct properly.

Why do they not reconstruct properly? Well often you need to take the sum or the difference of a 4D complex number Z and it’s conjugate that I write as Z* (because I cannot do ‘overline’ in this text mode). But the sum or the difference of such 4D numbers removes only the real part or the second imaginary part. The first and third imaginary parts stay in this sum or difference, this stuff is what makes the reconstruction of a signal s(t) going wrong.

Yet I was not crazy, as far as the reconstruction works it does it more or less as expected only you get only half of the signal reconstructed. That is not that worse but the garbage that enters the reconstruction is what makes this kind of making a 4D Fourier series something that will never have any practical benefit. But again does that mean the glass is half empty?

I remember that a long time ago in something like 1991 or 1992 I had found the product of a 3D complex number X and it’s conjugate X*. My naive idea was that this should only give the unit sphere in 3D space, but this product that also two imaginary components that I considered garbage at the time. Back in the time, it was just before the internet era, I could not know that this ‘garbage’ was actually the equation of a cone. And if you intersect this cone with the unit sphere in the space of 3D complex numbers, you get the 3D exponential circle. So it wasn’t garbage, it was the main prize in 3D complex number theory.
Back in the time in 1991 it was stuped from me to expect the 3D complex numbers would behave ‘just like’ the two dimensional complex numbers from the complex plane. May be in this year 2020 I am making the same mistake again by expecting a 4D kind of Fourier series must behave ‘the same’ as those defined on the real line (the original Joseph Fourier proposal) and the more advanced version from the complex plane.

With the 4D Dirichlet kernel just like with the 2D Dirichlet kernel from the complex plane, you must take the difference of a number and it’s conjugate. In the complex plane this makes the real component zero and this difference is just an imaginary number. The 2D Dirichlet kernel is the quotient of two such imaginary numbers and as such it is always a real number. For the 4D Dirichlet kernel stuff is not that easy but for me it was surprising that you can show relatively easy the 4D Dirichlet kernel has to be a ‘self conjugate’ number. That means Z = Z* (on the complex plane when you have a number z such that z = z* it means it is a real number).

This post is 8 pictures long, 7 of them have the standard size of 55×775 pixels but I had to make one picture both a bit more broad and higher in order to get the math fitting in it. Ok, let’s upload the math pictures with the stuff around the 4D Dirichlet kernel.

Do not fear if the 4D kernel looks a bit complicated, just take your time…
Yes trouble on the road, but it sure looks cute!

Ok, credits have to go to where that is deserved. I remember that back in the time like in 1990 I found it relatively hard to calculate the 2D Dirichlet kernel. It took me over 15 or 20 minutes but again: that was before the internet era. Yet at present day I was all so simple and why was that? That is because there is a nice Youtube video doing the easy stuff, it is from ‘Flameable math’:

May be at the end I can say the glass is half full because now this reconstruction stuff does not work properly, luckily I do not have to construct the Fejer kernel for 4D complex numbers…
Ok, let’s call it a day and let me end this post.

Definition of the 4D Fourier series.

4D complex numbers, Exponential circle, Exponential curves, Integration

I want to start with a bit of caution: In this post you can find the definition of the 4D Fourier series. It looks a lot like the definition as on the complex plane. But I still did not prove all those convergence questions. And I also do not remember very much from the time when I had that stuff as a student (that was about 30 years ago). So I don’t know if I will be able to make such proofs about convergence and what kind of functions you can use to make a Fourier series from etc etc.

Yet in this post I define a set of possible signals that I name ‘pure tones’ and these clearly have a 4D Fourier expansion because by definition they have a finite number of non-zero Fourier coefficients. Of course when you only have a finite amount of non-zero coefficients, you don’t have any kind of convergence problem. So for the time the convergence problems are avoided.

In this post, number 154 already, I hope I demenstrated enough that the basis functions used in the definition are all perpendicular to each other. After all that was a nasty hurdle we met when it was tried with just the four coordinate functions of the 4D exponential curve as our basis vectors. So we do not meet that problem again using the exponential curve as a whole. If I denote the exponential curve as f(t), the basis functions we use are basically f(nt) where n is a whole number. Just like in the previous posts I always use the notation f(t) when the period is related to the dimension and g(t) when the period is different. Here I use of course a period of two pi because that is convenient and it makes the coordinate functions more easy to write out: the first one is now cos(t)cos(2t) and the other three are just time lags of the first one. But if you want to write g(t) as an exponential, because of the period it now looks a bit more difficult compared to just e to the power tau times t.

For myself speaking I have no idea at all if crafting a Fourier series like this has any benefits of using just the definition as on the complex plane. After all I only have more or less basic knowledge about the use of Fourier series, so I just don’t know if it is ‘better’ in some regards and ‘worse’ in others.

At last without doubt under my readers there will be a significant fraction that wonder if those 4D complex number system is not some silly form of just the complex plane? After all if that 4D space is based on some imaginary unit l with the property that now the fourth power l^4 = -1, how can that be different from the complex plane? The answer to that lies in the logarithm of the first imaginary unit l. If this 4D space was just some silly extension of the complex plane, this log of l should be nicely bound to i pi/4 where i is of course the imaginary unit from the complex plane. But log(l) is the famous number tau because with that you can make the exponential curve f(t) = e^(tau t). Basically the main insight is that i pi/4 makes the complex exponential go round with a period of four because i^4 = 1 and the 4D number tau makes the exponential curve go round with a period of 8 because l^8 = 1.

This post is six pictures long, all 550×775 pixels in size.

The next picture is not written by me, I just did a ´copy and paste´ job.
Ok, we proceed with the ´pure tone´ stuff:

As usual I skipped a lot of stuff. For example, how did Fourier do it? After all at the time all this stuff with inner products was poorly developed or understood. That alone would be a cute post to write about. Yet the line of reasoning offered by Joseph Fourier was truly brilliant.
In case you are lazy or you want to avoid Google tracking you, here is a link to that cute symbolab stuff: symbolab.com
Link used: https://www.symbolab.com/solver/fourier-series-calculator

Ok, that is what I had to say for this tiny math update.

The last details before we finally can go to the new way of 4D Fourier series.

4D complex numbers, Exponential curves, Integration

This evening I brewed a fresh batch of wort, it is now cooling and tomorrow when it is at room temperature it can go into the fermenter bottles. Everything is relaxed around here, in the last week in my city only four cases of COVID-19 into the hospital.

Orginally I planned to define the 4D way of taking a Fourier series in this post, but while writing this post I realized to would become too long. So this post is seven pictures long (all 550×775 pixels) therefore I hope it does not cross the length of your attention span. For myself speaking always when I read some stuff that is ‘too long’ I start scrolling till the end and as such you often miss a lot of important details.

An important feature of exponential curves is that you have those de Moivre identities that come along with all those exponential curves. In this post I did not prove the 4D version of a de Moivre identity for the 4D complex numbers, but I give some numerical evdence. It has to be remarked that when I wrote the 20 posts around the basics of the 4D complex number system, I did not include the de Moivre identity. So that is more or less an ommision. On the other hand it is of course much more important to be able to find the exponential curve in the 4D space that is the basic material needed to write down such a de Moivre identity.

I categorize these posts about the 4D Fourier series also under ‘integration’. Not that I have many fantastic insights about integration but the reason for this category is much more down to earth: You have to perform an integration for every Fourier coefficient you calculate. In case you missed it: this year I finally wrote that post about how to define integration in the 3D complex numbers. Use the search function of this website in order to find that post in case you are interested.

Ok, that is what I had to say. Let us go to the beef of this post number 153 and that is of course the seven pictures that are all hungry for your attention. Here are the seven pictures:

Although I only gave some numerical evidence, the de Moivre identity is important!

There is an online Fourier series applet as it is named in these years. In the past we did not have applets but only computer programs. Anyway it is important those applets are there so I want to give a big thumbs up to the people that maintain that website! Here is a link to the Fourier thing:

Fourier series calculator. Link used: https://www.symbolab.com/solver/fourier-series-calculator

At last I want to point at the importance of such free websites. It is very good if a society has enough of this kind of ‘free stuff’. For example when in the year 2012 I picked up my study of the 3D complex numbers for me it was very important that there were free online applets for the logarithm of a matrix. Without such a free website I would have taken me many more years to find those exponential circles & curves. Or I would not have found them at all because after all my biggest breakthrough was when I did read that numerical evidence from log j on the 3D complex numbers: why are the two imaginary components equal I was just wondering? Later I found how crucial that was: only if the imaginary components are equal the eigenvalues are purely imaginary in the complex plane.

So I am breaking a lance for free websites where you can find good applets (read: computer programs) that help your understanding of math.

Ok, that’s it for this post. In the next post I will finally give that definition and after that I do not have a clue. I still do not have any good proof for convergence of these 4D Fourier series so we’ll see. Till updates.

New way of Fourier series using the 4D complex numbers.

4D complex numbers, Exponential curves, Integration

Warning: This post contains stuff that is not correct! Yet I decided to post it anyway so you can see that crafting math is also just keep on working until you have it right. The reason it does not work in the post below is that the basis functions I use are not all perpendicular to each other. And if you want to reconstruct a function or a signal s(t) with the basis functions as mentioned below, you will get weird overlap and the end result will not be correct.

Ok, that was a bit frustrating. But all in all I don’t have much reputation damage because more or less instantly I found another way of crafting the 4D Fourier series and that seems to work perfectly. So compared to the professional math professors who at one point in time accepted the quaternions and together with that stupid theorem of Frobenius concluded that 3D or 4D complex numbers are not possible, at least I don’t look that retarded. Sometimes I can be stupid too but at least it does not last for over one century. And may be that is also the reason that professional math professors absolutely do not want to talk about my work on 3D & higher dimensional number systems; admitting that you have been stupid for over one century is of course not an easy thing to do. And given the fact I am now unemployed for 17 or 18 years, rather likely the professional professors would rather be eating dog shit compared to speaking out my name… Once more we observe that in this world there is never a shortage of idiots.

In this post I use the coordinate functions of the exponential curve in the 4D complex numbers but I changed the period to 2 pi instead of a period of 8 that comes along with taking the log of the first imaginary unit. I also would like to mention that I use the so called modified Dirichlet kernel and because that kernel originates from Fourier analysis you must not get confused by the name ‘Dirichlet kernel’. The modified kernel is important (anyway for me) because it spits out all those coordinate functions for making exponential circles and curves in all dimensions possible. While if memory serves, the use of the Dirichlet kernel inside Fourier analysis is for using it in proofs of convergence. But may be I remember that completely wrong, after all it was about 30 years ago that I studied the Fourier stuff for the last time. The last two weeks were pleasant from the mathematical point of view, all that old Fourier stuff that somewhere still lingers around in my brain. But so much is gone, what is that Gibbs overshoot? Is that when a male math professor has his yearly orgasm? And what was the Parcival identiy? I don’t have a clue whatsoever.
This post is 7 pictures long, four are of 550×775 pixels and I had to enlarge the other three to a size of 550×850 pixels. So it is not a mess like the previous post where I just enlarged the pictures on the fly until all that text was there. Here it is:

Again, this way of recontruction does not work!

Likely all those basis functions have this problem, if you take the inner product of an arbitrary basis function against the same basis function with three times the speed, it is not zero. And as such it is not perpendicular…

For people who have never heard of inner product spaces done with functions I found a cute pdf where a lot of the basics are explained.

Inner product spaces.

I would like to be the 4D Fourier stuff done in a correct manner in the next post but sifting through what I wrote on 4D complex numbers I realized I never wrote about a de Moivre identiy for the 4D exponential curve. May be I will publish that in a separate post, may be not.
Anyway, have a good time and see you in the next update.

Two parametrizations for 3D exponential circles.

3D complex numbers, 4D complex numbers, Exponential circle, Exponential curves

It is about high time I post the solution in parametrization form of those five equations from 03 Oct 2019. That is almost 2 months back and oh how ashamed am I for my laziness… But for me math is a hobby, an important hobby but a hobby anyway. So other hobby’s are allowed to interfere with my little math hobby.

This post is 10 pictures long and at the end there is a horrible bad video from the Youtube channel Seeker. Begin this week I crossed that video with an intriguing title; Could These Numbers Unravel New Dimensions in Space? I was just curious but it is that Cohl Furey stuff again. It is an attempt to explain particle physics via complex number, quaternions and octonions… What do they have in common? These number systems are always fields that means all non-zero numbers have an inverse. Why the professional math professors find that so important is unknown to me, it is more like they have nothing else in the toolbox. If you are interested you can find the Cohl Furey video’s on Youtube.

In this post I too write about things that are common in the complex plane, complex and circular 3D numbers and 4D complex numbers. You can use the modified Dirichlet kernels as the building blocks for all possible exponential circles or in the case with 4D complex numbers: the exponential curve (in 4D space the curve is in a 3D hyper plane).

But I also wanted to show you the original cosine solution that I found years ago. To this day it is still amazing that the cosine can pull it off; that the cosine can be a building block for a 3D exponential circle. Next year it will be three decades ago when I found the 3D complex numbers and got interested in them. At present day you can wonder why there is never a healthy response from the math communuty. It is all very logical: if there is no healthy response that means the math community in itself cannot be healthy. It is just a community of perfumed princes and that’s it.

After so much blah blah it is high time to go to the ten pictures:

So from the complex plane in two dimensions to 4D complex space; a binding element is how you can use the modified Dirichlet kernels and their time lags to construct these very interesting parametrizations. Of course there is much more that binds those spaces together; the matrix representations are all very similar, just like the eigen values and eigen vectors. But above 2D it is never a field. And again why the professional math professors have this weird fixation on fields is completely unknown to me.
At last, here is that wonderful video that will make your toes curl

End of this post and thanks for your attention!

Part 19: Four integrals defining the 4D complex number tau.

4D complex numbers, Exponential circle, Exponential curves

It is a bit late but a happy new year anyway! In this post we will do a classic from the complex plane: calculation of the log of the first imaginary unit.

On the complex plane this is log i and on the complex 4D space this is log l .

Because this number is so important I have given it a separate name a long long time ago: These are the numbers tau in the diverse dimensions. In the complex plane it has no special name and it simply is i times pi/2.

On the real line it is pretty standard to define the log functions as the integral of the inverse 1/x. After all the derivative of log x on the real line is 1/x and as such you simply define the log to be the integral of the derivative…

On the complex plane you can do the same but depending of how your path goes around zero you can get different answers. Also in the complex plane (and other higher dimensional number systems) the log is ‘multi valued’. That is a reflection of the fact we can find exponential periodic functions also known as the exponential circles and curves.

The integrals in this part number 19 on the basics of 4D complex numbers are very hard to crack. I know of no way to find primitives and to crack them that way. May be that is possible, may be it is not, I just do not know. But because I developed the method of matrix diagonals for finding expressions for the value of those difficult looking integrals, more or less in an implicit manner we give the right valuations to those four integrals.

With the word ‘implicit’ I simply mean we skip the whole thing of caculating the number tau via matrix diagonalization. We only calculate what those integrals actually are in terms of a half circle with coordinates cos t and sin t.

This post is 8 pictures long in the usual size of 550 by 775 pixels (I had to enlarge the latest picture a little bit). I hope it is not loaded with typo’s any more and you have a more or less clean mathematical experience:

End of this post.