Monthly Archives: August 2017

It is cucumber time; I am lazy to the bone and just chilling out…

Uncategorized

Often when I am out I try to do a bit of math while riding my noble iron horse known as that old bicycle. The disadvantage of doing math on your bike is that one the one hand you cannot go very towards complicated stuff where you need pencil and paper but on the other hand you can get deep by getting some good idea’s.

And only when you get home and you have access to pencil & paper you can check if the stuff can be written out and see how your idea’s survive in the battle for attention from your brain.

After the previous post about magnetism I was only thinking ‘Why not do some pure 3D complex number stuff again’? But the math well is a bit dry lately when it comes to 3D complex numbers. May be this has a bit to do with the total and utter silence from the so called ‘professional math people’ who excel in staying silent…

But a few times it crossed my mind to do that mind boggling factorization of the Laplacian once more; if I would make a top 10 or top 25 list of the most strange results found this factorization of the Laplacian would end very high.
Yet when I check my own website, all that has to be said was already said about one year ago; on 05 August 2016 I posted the next seven pictures long post upon the factorization of the Laplacian using so called Wirtinger derivatives.

It still is a good read I think:
Wirtinger derivatives and the factorization of the Laplacian.

Wirtinger derivatives and the factorization of the Laplacian.

So there was little use in writing that stuff out again when there is, as usual, never ever any signal from the ‘professionals’ who rather likely are busy spending their too large salaries on stuff they think is important…

__________

In another development I came across the latest video from the Mathologer, it is very interesting because he claims that the famous Euler identity is not from Euler at all.
But Mr. Mathologer comes up with what is one of the famous Euler stuff, anyway a long long time ago it was one of the details that made Euler famous was finding what the sum of squared reciprocals was: 1/1^2 + 1/2^2 + 1/3^2 + ….

Over 25 years back I did the same calculations as the Mathologer invites you to so let me share the video with you. At first it looks a bit difficult but all you need to do is think about how to write out those infinite products as sums and after that you apply the age old trick of equalling the left and right side of the equation.

Here is the vid:

Euler’s real identity NOT e to the i pi = -1

May be in a future post we will be diving a bit deeper into this because Mr. Mathologer has nice news upon who found what but he skips all that stuff like how to write the entire functions from the complex plane as (infinite) products.
Furthermore he does not explain as why the given infinite product would be valid anyway…

Ok, may be in a next post I will be diving a bit deeper in all those kinds of infinite products.
Or may be it will be something completely different, anyway till updates.

Update from 22 August 2017:

By sheer accident while I was only watching a video about why there is such a break between higher math and higher physics, I came across some weird stuff from a guy named Edward Witten.
And the talk was about so called Seiberg-Witten monopoles, so my interest was aroused because I cannot allow plagiarism of course.

Anyway it turns out that Mr. Witten and his Seiberg pal talk about massless monopoles without laughing. The concept of a massless monopole is so idiot that normal people with just a tiny bit of self respect would never talk about that.

Anyway to make some long story short, Mr. Witten is also Mr. String Theory. You know that kind of theory that is impossible to validate in physical experiments so it is the opposite of what I do because if electrons carry magnetic charge it could be found in more and more experiments…
But the Witten guy wrote about Dirac operators and once more my interest was aroused and I looked it up: Dirac operators are differential operators D and if you square them you get the Laplacian…..

Here is a short wiki about the stuff involved:

Dirac operator
https://en.wikipedia.org/wiki/Dirac_operator

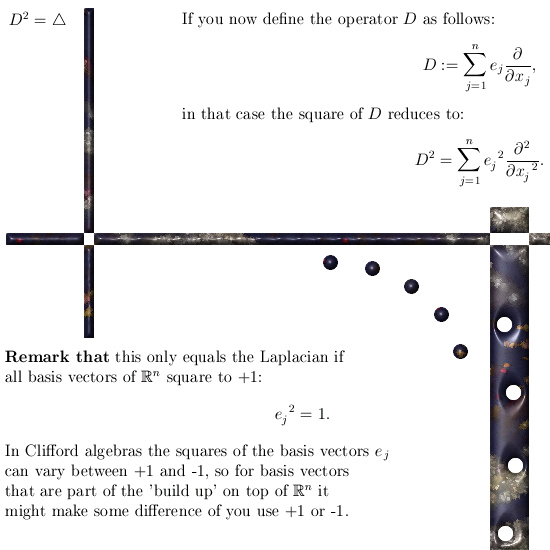
Basically when you try to find operators D that square to the Laplacian it is more like ‘operator problem looking for a fitting math space’ while in my above factorization of the Laplacian it is a math space (3D complex and circular numbers) that want a factorization.
In the wiki you also observe in example number 4 that Clifford algebras are named a possible candidates, that is true but a few remarks are at their place.
That is the content of the next two small pictures:

Ok, this wasn’t how I more or less planned the next update but when idiots come along talking about massless monopoles beside having deep fun I also have the right to expose the names of the idiots in question…

Let’s leave it with that, till updates my dear reader.

More on the failure of IBM’s racetrack memory.

Magnetism

Just over one week ago I posted reason number 48 as why electrons cannot be magnetic dipoles over on the other website, it is about the failure of IBM in crafting a new kind of fast memory. They failed because they treat electron spin like it is a vector while it makes much more sense that electron spin is one of two possible magnetic charges.

Here is the post from the other website:

Reason 48: The failure of IBM’s racetrack memory.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff02.htm#24July2017

It took me relatively long to find where the stuff all went wrong, at first I spend over a week every evening trying to find some stuff on the preprint archive and although there are some explanations found over there, because the writers of those articles are professional physics people they do not understand electron spin.

Also they DO NOT WANT TO UNDERSTAND ELECTRON SPIN because if you view electron spin as a magnetic dipole you end up in a gigantic ocean of nonsense, for example in the science of chemistry very often the electron pair plays a major role in the binding of all kinds of molecules. But if electrons were magnetic dipoles there would be no reason at all to limit the number of electrons to two; you would get all kinds of weird constellations of triplet electrons or whatever you can make with dipole bar magnets…

But if electrons carry two different magnetic charges suddenly it makes a whole lot of sense that we only observe electron pairs; the magnetism is neutral in an electron pair while the repelling electrical charge ensures no larger configurations beyond the pair formation are found. With a magnetic dipole you just would not observe this kind of behaviour…

Now back to IBM’s racetrack memory: All the time I did not understand how the IBM research folks did write the electron spin domains on the racetrack memory; electrons behave very much like cats:
It is easy to chase a cat into a tree but very hard to convince the cat it should leave the tree and come down to earth again…

With electrons you have the same: the two magnetic charges on the electron have a slightly different energy level, when an electron falls from the highest energy level to the lower one we observe the famous 21 cm wavelength photon. It is a well known fact from astronomy that interstellar and intergalactic hydrogen atoms only very very seldom have their electron fall from the highest magnetic energy level to the lowest energy level. This is what I name the ‘combed up universe’; even in intergalactic space most electrons are in the highest energy state because there are plenty of photons flying around to keep them ‘combed up’ when it comes to energy levels…

Back in the year 2004 IBM patented so called racetrack memory; the goal was to leave the 2D structure we have in present day computer hardware and use nano wires to go 3D and as such exploit three dimensional architecture of future computer hardware. The racetrack memory is made from nano wires, those nano wires contain lots of magnetic domains but contrary to the magnetic domains you find in, for example, iron these domains contain only one spin state.

According to IBM researchers all spin states are in the direction of the nano wire (from that you can understand they think electron spin is a vector, the vector represents the magnetic bipolar nature of the electrons according to IBM researchers).

In the next picture you see a boatload of information; the red and blue colour represents of course the two magnetic spin states of the electron. As you see on inspection they can inject blue electrons from the left and red electrons from the right.
If the IBM researchers inject red or blue electrons they can shift the entire column of electrons in the nano wire, according to IBM fellow Stuart Parkin the borders between the magnetic domains get transported…

Of course back in the year 2004 IBM thought they had hit the jackpot because if you neatly follow the standard model of physics where electrons are always having two magnetic poles you will always have that such borders are North pole against North pole (or South against South pole) and as such these borders should be extremely fragile…

And IBM thought they could transport those fragile things at high speeds, if true they would earn not billions but trillions over the long run of a patent.

Yet in my theory of magnetism, if it is true there are two magnetic charges the borders between red and blue magnetic domains are the most strong structures into the nano wire anyway so it is logical they keep intact while the electron column is transported…

Here you see why it is important to keep an open mind on electrons spin because if you follow the standard model companies like IBM cannot make technical progress.

For myself speaking I did not understand how to write information to the nano wire; I was thinking they did it with electro-magnetic radiation because any photon with a wavelength below 21 cm could bring an electron from the lowest energy state to the highest energy state…
But how to go from high energy to low energy is like talking to a cat high in a tree…

And no matter how much articles I did read on the preprint archive, nowhere an answer was to be found…
In the next picture you see how IBM visualizes how a small red region from the nano wire turns into blue: IT IS THAT WRITING WIRE BELOW WITH RED ELECTRONS IN IT!!!!!

Picture source:

Now we have two clashing versions on electron spin:

  1. The standard model version where electrons are magnetic dipoles says: The red writing wire cannot change the red domain in the nano wire because all red electron spins point into the same direction. And if you add more bar magnets perfectly aligned that only makes the red state stronger. Versus:
  2. If electrons carry one of two magnetic charges and we use the principle that like charges repel, the red electrons on the writing wire repel the red electrons in the nano wire into the blue neighbouring blue domains. At the same time blue electrons will flow to the red region.

So if my view on electron spin is true, in that case the simple act of writing information to such nano wires destroys the information in the surrounding magnetic domains.

And that my dear reader is something that the professional physics people still do not want to acknowledge until this present day of 03 August 2017.

By the way, next winter it is about the fourth or even the fifth year I am explaining as why electrons cannot be magnetic dipoles. Those people, the so called ‘professionals’ will keep on hanging to their silly beliefs around electron spin for a much longer time.

Let’s leave it with that.