Since this is the post number six on the Fermat stuff already, I decided to create a new category for this kind of math. It is no secret my knowledge of algebra is rather rudimentary, a lot of things in algebra are things I do not like to study or think about. I always had trouble learning algebra, often those people come up with say 15 definitions of algebra objects but all those definitions have the weight of a fly and rather soon I am lost in the forest. I much more prefer more heavy definitions of math objects (like the Cauchy-Riemann equations) and not stuff that is a semi-simple defined on a semi-simple kind of curve…
So I do not know much about number theory, a few days ago I downloaded the entire proof of Andrew Wiles where he proves that the last theorem of Fermat is actually true. Well already in the very first line I get lost; and in that proof you have all that Galois stuff so I think that I skip that entire proof for the time being.
A lot of things are weird in number theory. For example that Frey elliptic curve is based on a hypothetical solution to the Fermat equation a^n + b^n = c^n. If you interchange a and b in the Fermat thing, every thing stays the same. But you get a different elliptic curve if you interchange a and b in that Frey ellipic curve. So I just had no clue; wtf is going on here? Luckily I found a video of Gerhard Frey explaining a bit about what and why and the elliptic curve he defined is done in that way so that the discriminant can be simplified using that theoretical solution to the last Fermat theorem. So it is not crazy but it has it’s own logic, yet search for yourself: how many texts are there that speak about this Frey elliptic curve and actually tell you this? Most math writers simply repeat the (old) knowledge and are bad at explaining why stuff is such and so.

I always work alone, actually it is not work but an important hobby, and because I have to figure out every thing alone I have no access to people with a lot of knowledge on the details & the broader lines of some kind of math theory. Because I work alone this often takes more time. Yet on the universities where the people are supposed to work together they have never found 3D complex numbers or counter examples to the last Fermat theorem. In other sciences like physics it also goes like crazy if you read what they made of electron spin in 100 years of time. So working together is not a guarantee of speeding things up. On the contrary if after a full century you still think that, for example, the electrons is a magnetic dipole you are crazy to the bone.

This post is a short one, only four pictures long. I nicely work out what that discriminant is supposed to be. Likely people like Andrew Wiles and Gerhard Frey have never seen counter examples to the last theorem of Fermat, so why not at the end of my post take a look at what happens in that case? Well it does not look very promising for the collective of overpaid math professors; such a determinant of the Frey elliptic curve is always zero… Anyway on all spaces I found where we have counter examples to the last Fermat theorem, such a discriminant is always zero.
And that is regardless of the last Fermat theorem counter example being true or false; sorry Gerhard Frey I don’t think this approach will bring any fruits at all…
Well here are the four pictures, all of the standard size of 550×775 pixels.

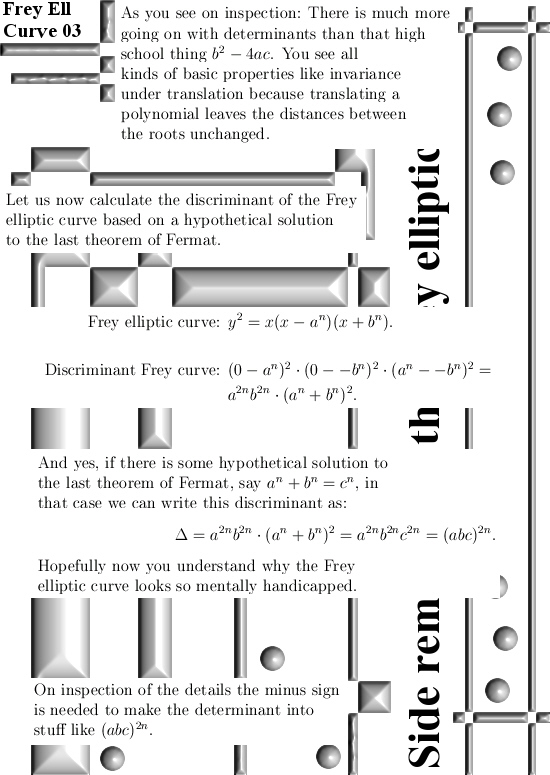
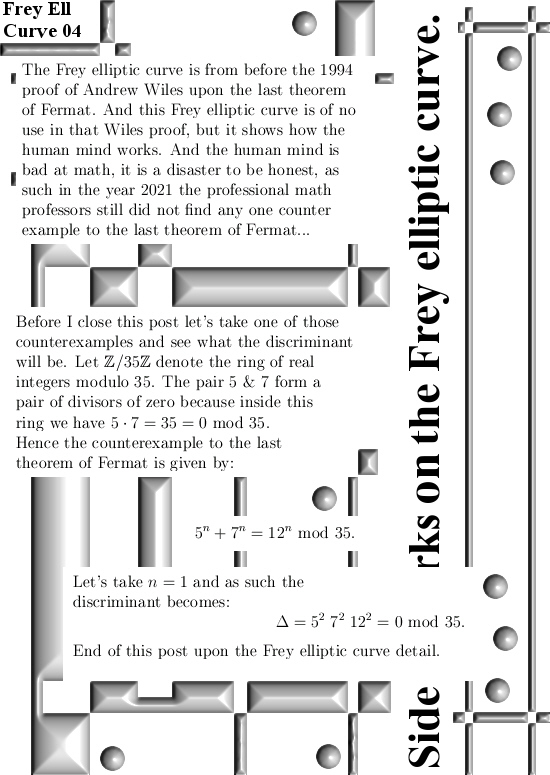
The only reason I wrote six posts on the Fermat stuff is that those counter examples like 5^n + 7^n = 12^n modulo 35 are too cute to ignore.
End of this post, thanks for your attention.