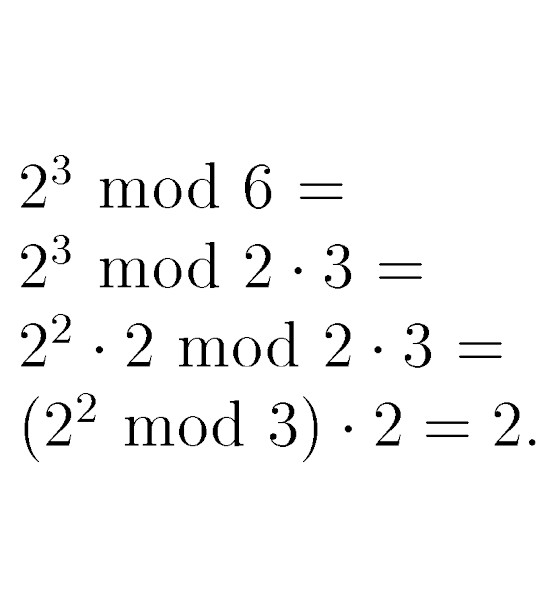Monthly Archives: June 2021

Oversight of all counter examples (until now) to the last theorem of Fermat.

Last Fermat theorem

Once more I estimated my writer skills too positive; I thought it takes only 7 to 8 pictures to pen down all counter examples to the last theorem of Pierre de Fermat. But I had to stop because this post already is 10 pictures long. I organized the stuff around so called ‘levels’ so we have Level zero counter examples (the most basic ones) to level four counter examples (the most complicated ones) to the last theorem of Fermat.
We are now almost half a year further down the timeline since I looked at that video of Andrew Wiles and while looking at that video I already constructed the first counter example to the last theorem. And now we are about half a year further I have arrived at the conclusion that inside the math community there are no accepted counter examples known or discussed or whatever what they do with it. So I am not expecting my counter examples will find the place they more or less should have, acting as an adult is never within reach of the math professors.
Likely if you (as a math student or so) show these counter examples to one of your math professors, it might be it gets instantly rejected because ‘this is modulo calculus’ and has ‘nothing to do with the last theorem’. But in a pdf from Gerhard Frey (the guy from the Frey elleptic curve) I came across the next hilarious screen shot:

This is hilarious; Modulo arithmetic is allowed?????

Of course people like Andrew Wiles or Gerhard Frey will never ever react; they are perfumed princes and those high nobility people do not mingle with the plebs, farmers and peasants.
Does the absence of counter examples on the internet indicate that the math hot shots also have an absence of counter examples in their holy brain tissue? It looks like it, of course it is very well possible plenty of people found those counter examples in the past but they got only a fresh dose of what I experience for say 30 years: You get one 100% neglected all of the time. After all if you are an outsider like me, the collective of math professionals acts very much like a secretive incest club. Those kind of clubs are not very open to communication with the outside world. Not that math professors are pedophiles but the behavior is keeping things inside is very much the same.
An interesting question is if perfumed prince Andrew Wiles knows these counter examples. My guesstimate is no. And why is that? After the pictures of the main post I will show you that video from the Abel prize lecture and there you can see Andrew formulating the last theorem of Pierre de Fermat. He does it more or less in the following manner:

For integers x, y and z with xyz not equal to 0, it is impossible that
x^n + y^n = z^n. This for integers n > 2.

If Andrew would have knowledge in his brain about these counter examples likely he would have formulated it like this:

For positive non-zero integers x, y and z, it is impossible that
x^n + y^n = z^n. This for integers n > 2.

All counter examples I found in the last five months have the property that xyz = 0 because say the x and the y form a pair of so called divisors of zero. (The level zero counter examples do not have this property, but I did not find the level zero examples myself…) Now it could be that Andrew is as evil as he is smart and formulated it with the xyz not zero way in order to subtlelly exclude my wild math adventures. But in reality it is much more likely that Andrew is just another perfumed Princeton professor. So my estimate is and stays that Andrew is not aware of the rather simple counter examples to the last theorem of Pierre de Fermat as found below…

Ok, this post is 10 pictures long and it only contains the stuff found that is based on modular arithmetic. In my view it is all rather basic and as such should explain itself. The main basis is that ‘divisor of zero’ stuff where two non zero numbers multiply to zero. For example if we take the real integers modulo 35, in that case if we multiply 5*7 we get 0 because 35 = 0 inside the ring of integers modulo 35. It’s all so basic that it makes you wonder once more: why is this not inside the math classes on universities? But for that answer you must ask the perfumed professors and the perfumed professors never answer because they are much more busy of getting a fresh stack of perfume. That’s life…
Have fun reading it

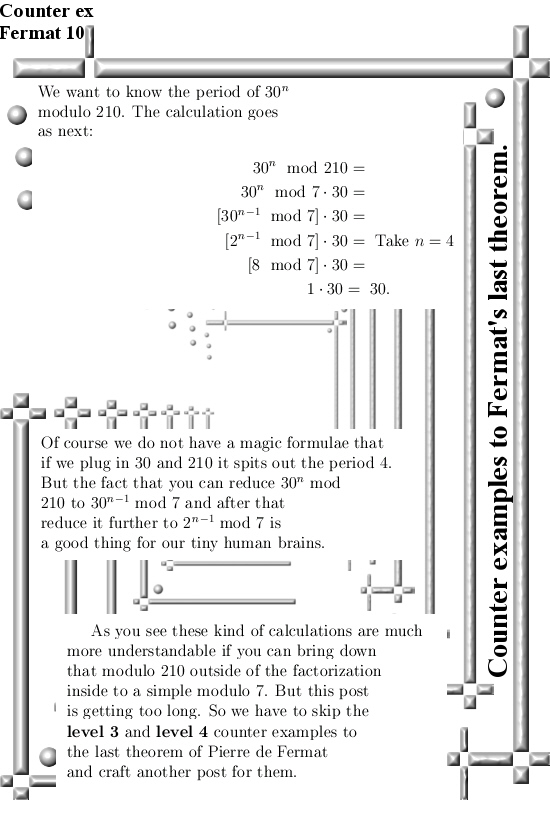
For me the only thing I learned while writing this post is that you can use that simple rule for writing 30^n mod 210 in stuff mod 7. It is the same kind of calculation as in the modified little theorem of Fermat and this is also a detail I could not find on the internet.
Oh yes now I am in a laughing mood: Can we prove the perfumed professors are indeed perfumed overpaid people? Yes we can: They will also not react of the modified or improved little theorem of Fermat. We will need a few years of time for that, but why should they react?

Ok, I promised you the video of a Princeton perfumed prince named Andrew Wiles, here it is and please pay attention to the way he formulates the present day formulation of the last theorem of Pierre de Fermat:

At only one minute into the video we observe that likely Andrew has no clue whatsoever about the above counter examples to the last theorem of Pierre de Fermat:

Why this way of formulating the problem?

End of this post. Thanks for your long lasting interest in these details on the last theorem of Pierre de Fermat.

What is a Dyson-Harrap satellite?

Magnetism

A few days back the folks from scishow space came with a rather brilliant concept of a so called Dyson-Harrap satellite. I have to say I do not understand all the details, for example you can indeed catch a lot of electrons from the solar wind but how do you make a current with them that goes round? After all an electric circuit should be closed so that the electrons if they go round can lower their electric potential.
They Dyson in the name of this satellite is more or less a honorary name, may be you know that name from the concept of a Dyson sphere.
Anyway the goal is to harvest the energy as found in the solar wind and since scishow is nice to watch, it is still a show and who not forget all kinds of important stuff like ‘Is the solar wind electrically neutral’ meaning there are as much electrons as protons? And if you catch it with a solar sail, where do the protons go? Well suppose it is all possible: you can catch solar wind and use that to make a closed electrical loop. Below you see a scetch of how this supposedly must work:

The blue line is a copper strip or wire and the current through it creates a cylindrical magnetic field. And because scishow is always more show as sci they simply say: “The electrons get deflected by the magnetic field and therefore create more electrical current”. Just like the solar wind ‘avoids’ the earth and people say “The earth magnetic field deflects the solar wind particles”. So we are supposed to believe that deflection explains why electron are attracted in the picture above while the earth pushes them away…
Of course electrons are magnetic monopoles, they come with a south pole or a north pole charge and as such they are always accelerated in the direction of the magnetic field lines. For example that explains why the earth pushes the solar wind away and it also explains why the electrons that make the aurora’s have the speed they have. They ionize the atmosphere because they have enough speed by the acceleration done by the earth magnetic field. So because we can see the aurora’s that detail alone shows that electron just cannot be magnetic dipoles as the idiots & retards from physics want you to believe.

Look at the picture above: The electrons enter that cylinder shaped magnetic field. According to their magnetic charge they are accelerated in the direction of the magnetic field lines or against that direction. So they go either left curved or right curved with respect to that blue copper wire. Now why do they go to the center? Very simple: There is the magnetic field stronger so of course they like to go there.

Compare that to nuclear fusion tokamak style: Why does the plasma not hit the wall in the beginning? Well the magnetic fields in those torus shaped vessels is stronger in the middle and this is why in the first few seconds they do not slam into the walls. But this post is not about the plasma instabilities in nuclear fusion reactors tokamak style, if the idiots & retards from plasma physics are that smart, they can figure it out for themselves. After about six years of explaining that electrons can’t be magnetic dipoles, what do the shitholes, idiots & retards from plasma physics do? Of course they do nothing, likely they make jokes among themselves as why I am the idiot & retarded person.
Well in 2025 it is expected first fusion plasma for the ITER thing and we will see who is laughing after that future colossal failure…

Sometimes I wonder if my own brains work so differently that it is me who is the crazy one. But I have a tendency of using logic, for example this website is about 3D comples numbers. Math professors think that 3D complex numbers do not exist. It is just another example of how people just don’t use logic but only emotion or if you want ‘group think’. Of course 3D complex numbers exist, you just do an imaginary component j to the third power and you get minus one: j^3 = -1. Just like the complex plane where you can find all your math fruits by using logic and i^2 = -1.
But math professors do not want to do that because they are rather retarded imbeciles too.
After so much social classifications, why not take the time and think a bit about the next satellite concept? Here is the vid:

To be honest I liked the video because it is so refreshing. For the time being I classify it more as science fiction and not a serious thing. Just like math professors are not a serious thing after 30+ years of total neglect of say 3D complex numbers.

Ok, the next post will be an oversight of all those counter examples to the last theorem of Pierre de Fermat. And oh oh oh, when I think about it: The math professors in 350 years of time have never ever found a good bunch of counter examples using only modulo arithmetic. Talking about a bunch of inbread retarded imbeciles, they even cannot explain stuff like:

2^3 mod 6 = 2 &
3^2 mod 6 = 3. (This is the little theorem of Fermat modified a bit.)

Even basic stuff like that, the math professors have no clue whatsoever but they think they are brilliant…
Let’s leave it with that my dear reader.
See you in the next post. (On 20 June added a small proof for the above modified little theorem of Fermat:)

The proof in the next picture is so simple that may be it is better to replace the factors 2 and 3 by p and q representing two different prime numbers for use in the modified little theorem of Pierre de Fermat. In the background of the picture you see two math professors discussing the details of the little proof to the modified little theorem. They seem to disagree on something, I do not have a clue whatsoever as why they seem to disagree. Is there something wrong with my little modification of the little theorem? May be it is better to leave the math professors alone. After all if you want to be a happy person you should not mingle with idiots all of the time. That does not bring happiness…

Without the two math professors it looks like this:

Ok, let this be the real end of this post. Thnx for your extra attention and in the next post I will try to give an oversight of all counter examples to the last theorem of Fermat I found during this year.

Two things and a proof that the 4D complex rationales form a field.

4D complex numbers, Exponential circle, Last Fermat theorem, Matrix representation

I finished the proof that was originally meant to be an appendix to the previous post. And I have two more or less small things I want to share with you so lets get started with the first thing:

Thing 1: Tibees comes up with a very cute program of graphing 3D surfaces. It’s name is surfer, the software is very simple to use and it has the giant benefit of making graphs from implicit equations like
f(x, y, z) = 0. For example if you want the unit sphere in 3D space you must do x^2 + y^2 + z^2 – 1 = 0. Now for this website I always used an internet applet that uses ray tracing and by doing so over the years such graphs always look the same. But this surfer program has cute output too and it has the benefit you don’t need to be online. Here is how such a graph looks, it is the determinant in the space of 3D complex numbers, to be precise it shows the numbers with a determinant of 1:

By the way, the surface of this graph is a multiplicative group on it’s own in 3D space. I never do much group stuff but if you want it, here you have it. And for no reason at all I used GIMP to make one of those cubes from the above graph. It serves no reason beside looking cute:

The Tibees female had a video out last week where she discusses a lot of such surfaces in three dimensional space using that surfer software. And she is a pleasant thing to look at, it is not you are looking at all those extravert males drowning in self-importance only lamentating shallow thoughts. The problem posed in the video is an iteresting one, I don’t have a clue how to solve it. Title of the video: The Shape No One Thought was Possible. It is a funny title because if you start thinking about all the things that math professors thought were not possible you can wonder if there is enough paper in the entire universe to write that all out..
Link to the Surfer program in case you want to download & install it:
https://www.imaginary.org/program/surfer.

So far for thing 1.

Thing 2: The last weeks it is more and more dawning on me that all those centuries those idiots (the math professors) did not find counter examples to the last theorem of Fermat. Nor was there any improvement on the little theorem of Fermat. Only Euler did some stuff on the little theorem with his totient function, but for the rest it is not much…
Well since Jan of this year I found many counter example to the last theorem of Fermat and in my view I made a serious improvement on the little theorem of Fermat.
So is the improvement serious or not?
Here is a picture that shows the change:

So it’s modulo ap instead of modulo p.

On a wiki with a lot of proofs for the little theorem of Fermat they start with a so called ‘simplification’. The simplification says that you must pick the number a between 0 and p. So if you have an odd prime, say a = 113, does the little theorem only make sense for exponents above 113?
And can’t we say anything about let’s say the square 113^2?

With the new version of the little theorem we don’t have such problems any longer. Here is a screen shot from the start of that wiki, the upper part shows you the improvement:

Here is a link to that wiki that is interesting anyway.

If you follow that link you can also scroll down to the bottom of the wiki where you can find the notes they used. It is an impressive list of names like Dirichlet, André Weil, Hardy & Wright and so on and so on. All I want to remark is that non of them found counter examples to the last theorem nor did they improve on the little theorem of Fermat. Now I don’t want to be negative on Dirichlet because without his kernel I could never have crafted my modified Dirichlet kernel that is more or less the biggest math result I ever found. But the rest of these people it is just another batch of overpaid non performers. It’s just an opinion so you don’t have to agree with it, but why do so many people get boatloads of money while they contribute not that much?

End of thing 2.

Now we are finally ready to post the main dish in this post: the proof that the subset of four dimensional rational numbers form a field. Math professors always think it is ‘very important’ if something is a field while in my life I was never impressed that much by it. And now I am thinking about it a few weeks more, the less impressed I get by this new field of four dimensional complex numbers.
Inside the theory of higher dimensional complex numbers the concept of ‘imitators of i‘ is important: these are higher dimensional numbers that if you square them they have at least some of the properties of the number i from the complex plane. They rotate everything by 90 degrees or even better they actually square to minus one.
Well one of the imitators of i in the space of 4D complex number is dependent of the square root of 2. As such it is not a 4D rational complex number. That detail alone severely downsizes my enthousiasm.
But anyway, the next pictures are also a repeat of old important knowledge like the eigenvalue functions. Instead of always trying to get the eigenvalues from some 4×4 matrix, with the eigenvalue functions with two fingers in your nose you can pump out the eigenvalues you need fast. This post is six pictures long each size 550×825 pixels.
Here we go:

Yes that is the end of this post that like always grew longer than expected. If you haven’t fallen asleep by now, thanks for your attention and don’t forget to hunt the math professors until they are all dead! Well may be that is not a good idea, but never forget they are too stupid to improve on the little Fermat theorem and of course we will hear nothing from that line of the profession…