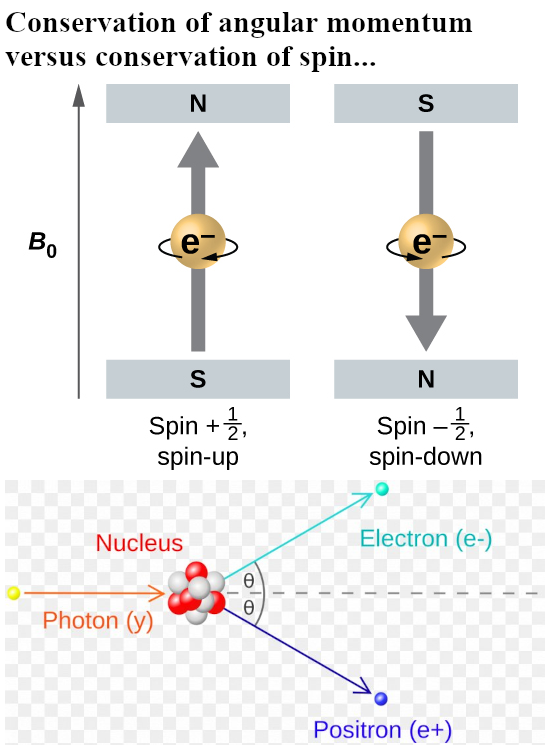
This is another very short post, the main text is 2 pictures and there is an additonal Figure 1 added. It is about the impossibility of having both spin and angular moment conserved in the electron-positron pair creation process. This is under the assumption that electrons are actually spinning and that this spinning causes the official version of electron spin: the tiny magnet model.
Of course there is nothing spinning, back in the time Wolfgang Pauli himself calculated that even if you concentrate all the electric charge of an electron on it’s ‘equator’, it must spin so fast that this is a huge multiple of the speed of light. A long time ago I did such a calculation myself, it is not very hard to do but I skipped it in this because that calculation has nothing to do with the content of the post. So you can easily do that yourself, after all it is just some advanced high school physics and if you do that the answer will of course depend strongly on how large you think the electron is if you view it as a tiny billiard ball.
The word ‘spin’ is a terrible wrongly chosen word to describe the magnetic properties of the electron. I have wondered so often as why the physics people think year in year out that the electron is a tiny magnet while you really do not need much brain power to see that this is nonsense. Beside all those fundamental energy problems there are also problems with the above mentioned conservation laws. The fact we have today so many people from the physics community talking about ‘the spinning electron’ is caused in part by that original stupid choice to name it ‘spin’. After all this word strongly suggests that we are dealing with tiny magnets, every electron must be a tiny bipolar magnet while if you view them as magnetic monopoles you don’t have all these weird energy problems.
In case you are new to this website: I think that electrons are magnetic monopoles, just like their electric charge, and furthermore this magnetic charge is permanent and as such it is impossible to flip the spin of an electron.
And if you are from the physics community yourself, may be you need to vomit from the idea that electrons are not tiny magnets. Or may be you pity me because I am a middle aged man and you think I want to save physics or the wider community known as humankind from wrong doing when it comes to electron spin. Well I have to disappoint you: I don’t give a shit about such stuff, ok in the beginning I did but after a few years I realized that likely physics will be trapped a few centuries longer before they start using logical thinking when it comes to electron spin.

In the two pictures below I also experiment a bit with using other backgrounds, here you see something like a big hand made with some generative AI video thing. May be it is time to replace my old background made with my old Windows XP computer by some fresh stuff.

This intro is getting far to long because I wanted this post to be short. So let me hang in the pictures and here we go:

In Figure 1 below all you see are two images I downloaded from the internet while using the search phrases as written above. You just never see those spinning arrows if you search for electron-positron pair creation. It is as so often: As soon as we get into crazyland, the physics people just don’t talk about it.

Well yes, this is indeed the end of this post.

Another short post, this time again on the totally crazy so called bonding and non-bonding pairs in theoretical chemistry. It is one of the many energy problems that come along if you want electrons to be tiny bipolar magnets. And if you view the electrons as magnetic monopoles, in that case all of a sudden you don’t have these kind of weird energy problems.

Lets dive into it, this post is 3 images long and here we go:

That’s more or less all I had to say today, if you view the magnetic properties of electrons as monopole magnets just like their electric properties the standard electron pair becomes the lowest (potential) energy state. Before I close this post let me quote from a wiki an interesting detail about the non-bonding electron pairs: they have a tendency to be outside the so called ‘bonding region’ between atoms in molecules. Once more this only makes sense when electron carry a monopole magnetic charge.

In theoretical chemistry, an antibonding orbital is a type of molecular orbital that weakens the chemical bond between two atoms and helps to raise the energy of the molecule relative to the separated atoms. Such an orbital has one or more nodes in the bonding region between the nuclei. The density of the electrons in the orbital is concentrated outside the bonding region and acts to pull one nucleus away from the other and tends to cause mutual repulsion between the two atoms. This is in contrast to a bonding molecular orbital, which has a lower energy than that of the separate atoms, and is responsible for chemical bonds.

Here is the link to the wiki I quoted from:
https://en.wikipedia.org/wiki/Antibonding_molecular_orbital

That’s it, see you in some other future post or enjoy some old posts on say the 4D complex numbers because they are beautiful and that is something we cannot say about the behaviour of the average physics professor with their weird fixation on electrons as tiny magnets…