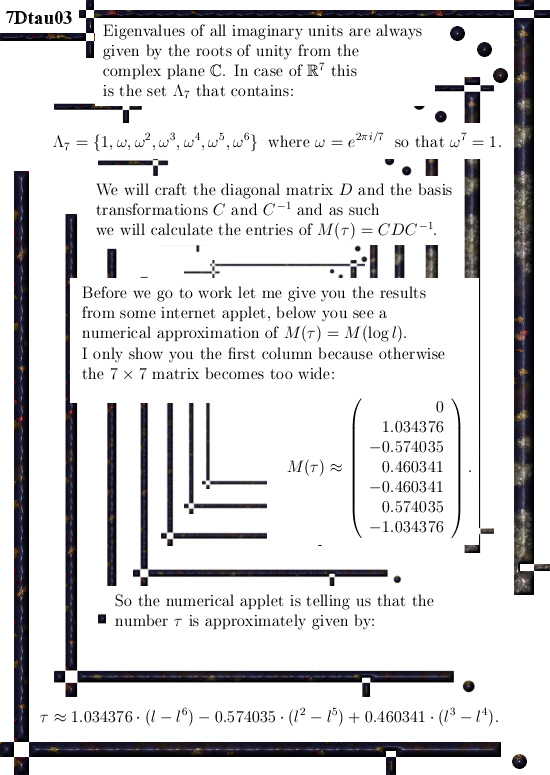
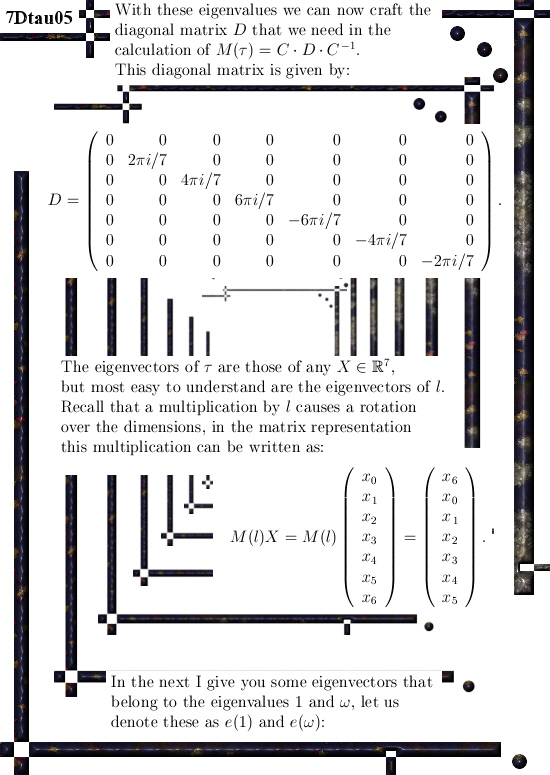
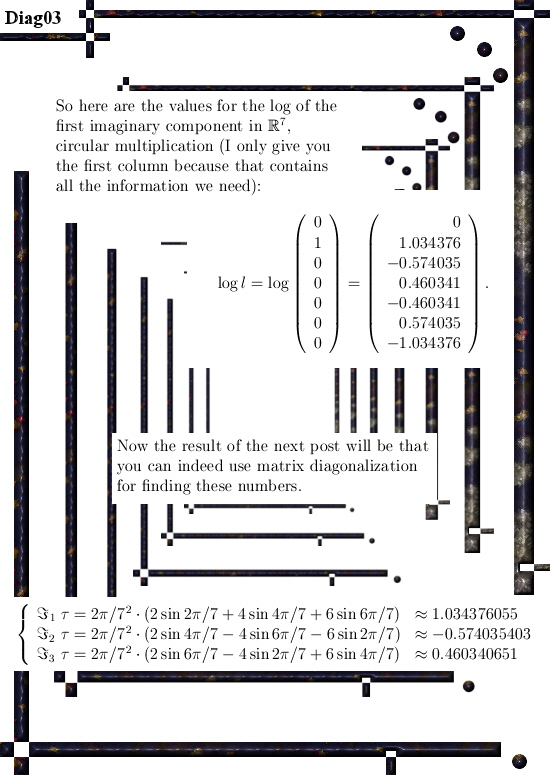
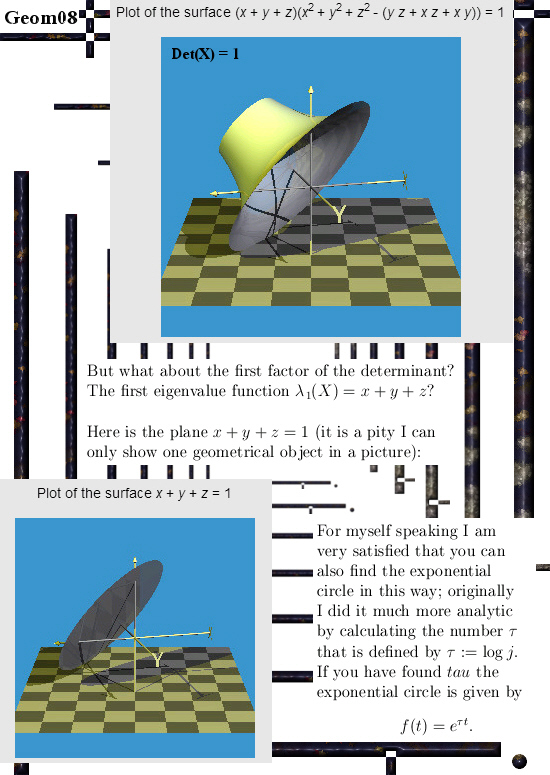
I just finished brewing the 100-th batch of a beer under the names Dark Matter and Spin 1/2 beer. All in all that is an amazing amount of beer; in the past I brewed 35 liter per batch but now it is 40 liter per batch so all in all an amount of something between 3500 and 4000 liters… So ein prosit my dear reader.
The ‘new’ roots of unity aren’t that new, this post is a re-editing of something I posted on 05 Jan 2014 on the other website. Later that year I started this website. Actually these roots of unity are just over five years old. In mathematical terms that is still very young so in that sense they are still new.
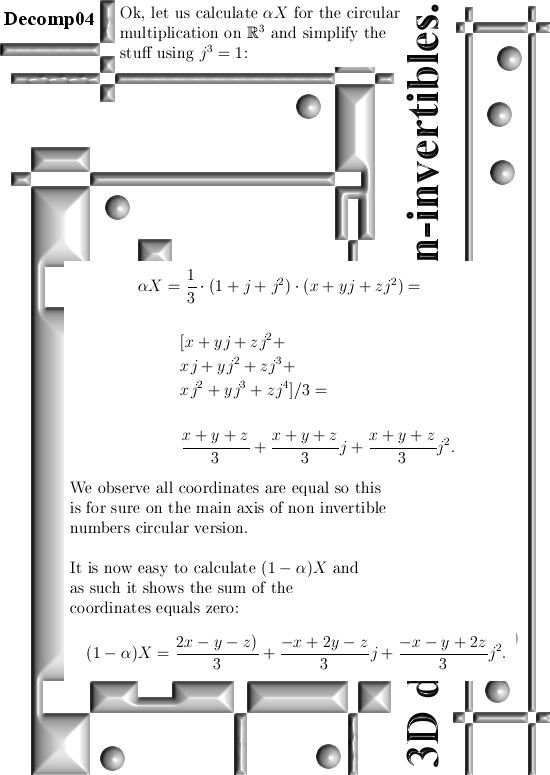
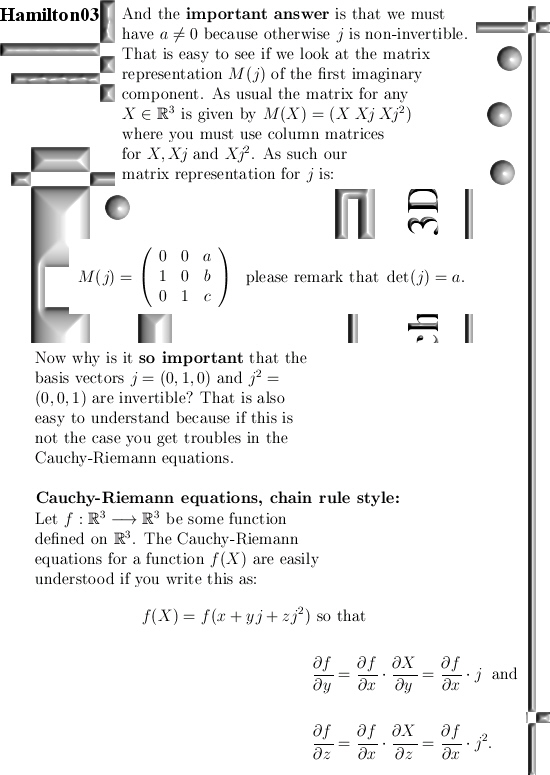
Recall the roots of unity in the complex plane are solutions to z^n = 1 and as such these roots are found on the exponential circle (the complex exponential) in the complex plane. As you have found the exponential circle or exponential curve in some space, from that you can always make new roots of unity. That is hardly a mathematical achievement because it is so simple to do once you have found your exponential circle or curve. But in the diverse spaces these new roots of unity behave very different, for example in this post we will add them all up but unlike in the complex plane they do not add up to zero. That is caused by the fact that in the complex 3D space the number alpha is at the center of the exponential circle, as such if we add n roots of unity in 3D space the result is n times alpha. Last year we studied the space of 4D complex numbers and if you would craft new roots of unity in that space it will behave much more like those in the complex plane because in the 4D complex numbers we have 0 as the center of the exponential curve. (For dimensions above 3 the exponential curve always lies in a hyperplane so it can never be a circle.) It always amazes me that you have all those physics people who study string theory but as far as I know never use exponential curves…
Life is beautiful, because how can you do string theory without math like that? But in physics almost everything is beautiful, for example if they explain the outcome of the Stern-Gerlach experiment always 50% of unpaired electrons align with the applied magnetic field and the other 50% for some mysterious reason do the anti-align thing. And if one hour later the same physics professor explains how a permanent magnet can attract some piece of iron, all of a sudden 100% of the unpaired electrons align and all that talk of 50/50 suddenly is not observed… Life inside the science of physics is wonderful; all you have to do is a bit of blah blah blah and if people complain this is not logical at all you simply say: Quantum physics is such that if you think you understand it, you don’t understand it… How wonderful is the life of physics professors; talk some blah blah blah and if people complain you blame them for ‘not understanding quantum things’. For sure that is a beautiful form of life.
But enough of the talking, somewhere in the next seven pictures I did forget to insert a graph of the determinant. Yet I showed you the structure of the non-invertible numbers so often, I think I post it with that fault included. After all why should life be perfect? If life would be perfect you would have no way of improvement and likely that is the moment you die: no more possibility of improvement. As usual the pictures are 550×775 pixels but I had to make the first one a tiny bit longer. Good luck with digesting it & have a bit of fun in the process.






For myself speaking it was fun to read my own two proof for the rain theorem again after five years. Please do not forget that new roots of unity on other spaces can be very different in behavior, after all they are always part of the exponential circle or curve in that space so they will derive their math properties from that. Till updates.