Category Archives: Exponential curves

Intro to the calculation of the seven dimensional number tau (circular version).

December 1, 20173D complex numbers, 5D complex numbers, Exponential circle, Exponential curves, Matrix representation, UncategorizedReinkoVenema

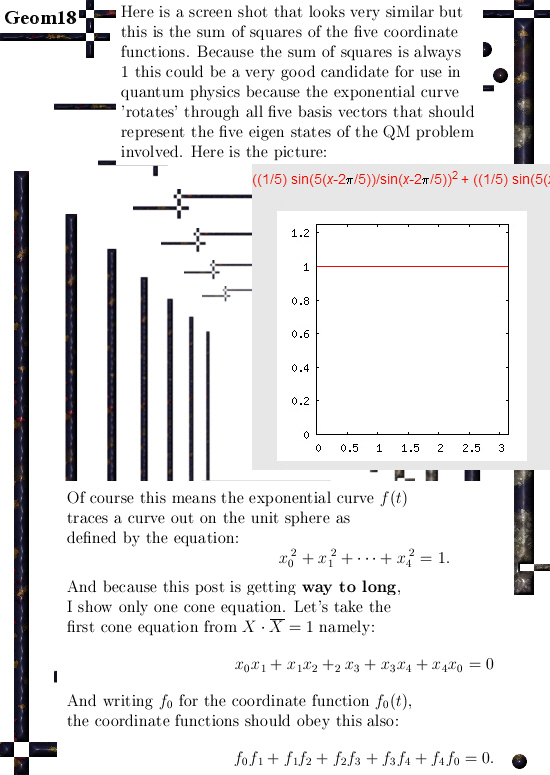
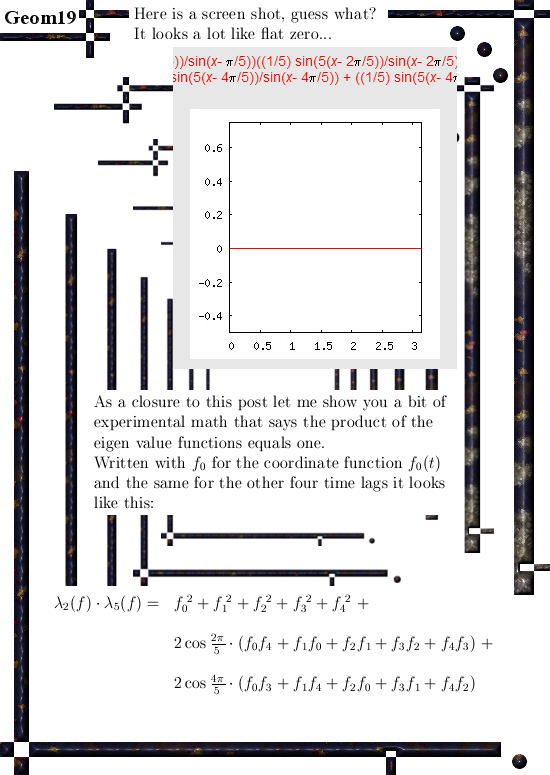
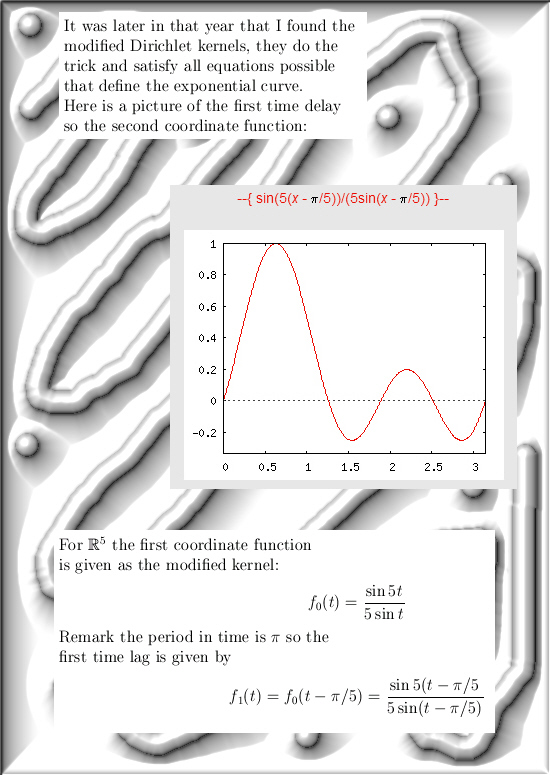
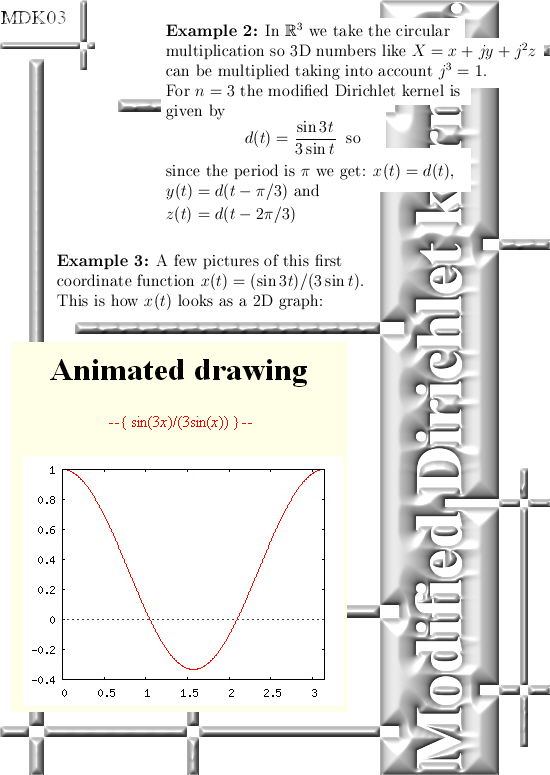
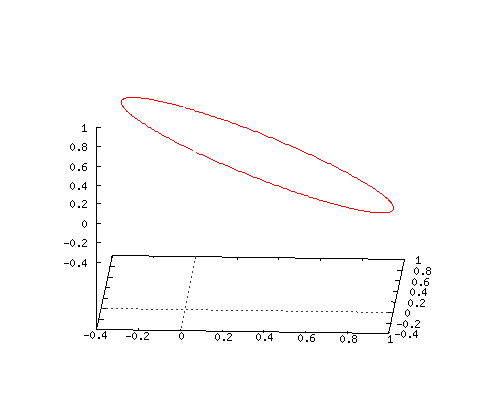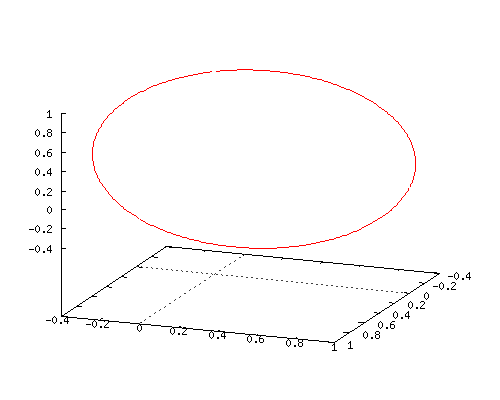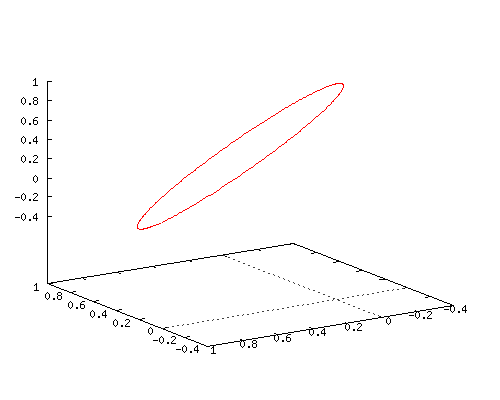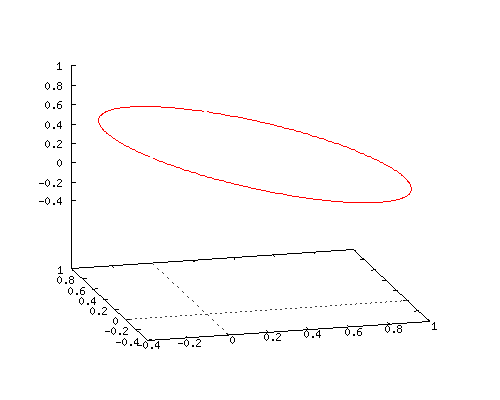
All details will be in the next post but I succeeded into using matrix diagonalization in order to find this seven dimensional number tau.
For people who do not understand what a number tau is, this is always the logarithm of an imaginary unit. Think for example at the complex plane and her imaginary unit i. The number tau for the complex plane is log i = i pi/2.

The problem with finding numbers tau becomes increasingly difficult as the number of dimensions rise. I remember back in the year 2015 just staring at all those matrices popping up using internet applets like the next one:

Matrix logarithm calculator (it uses the de Pade approximation)
http://calculator.vhex.net/calculator/linear-algebra/matrix-logarithm

Yet back in the year 2015 I was riding on my noble iron horse (a cheap bicycle) through the swamps surrounding the village of Haren and suddenly I had a good idea. Coming home I tried the idea of matrix diagonalization out in 3 dimensions and it worked.

I even wrote a post about it on 23 Nov 2015:

Integral calculus done with matrix diagonalization.

Now I think that most readers who visit this website are familiar with the concept of finding a diagonal matrix D containing all eigenvalues of a given matrix M. Once you have the eigenvalues you can calculate the eigenvectors and as such craft your matrix C containing all eigenvectors.
You can write the stuff as next: D = C^-1 M C.

Suppose you don’t know what M is but I give you the matrices D, C and the inverse of C. Can you find the matrix M?

Yes that is a beerwalk, all you have to do is calculate M = C D C^-1 and you are good to go.

But with the logarithm comes a whole lot of subtle things for making the right choice for the eigenvalues that you place inside the diagonal matrix D. It turns out you only get the desired result if you use arguments in the complex plane between minus and plus pi.
This is caused by the fact that you always need to make a cut in the complex plane if you want to work with the complex logarithm; but it is a bit surprising that only the cut where you leave out all real negative numbers (and zero of course) makes the calculation go perfect and in all other cases it ends in utter and total disaster.

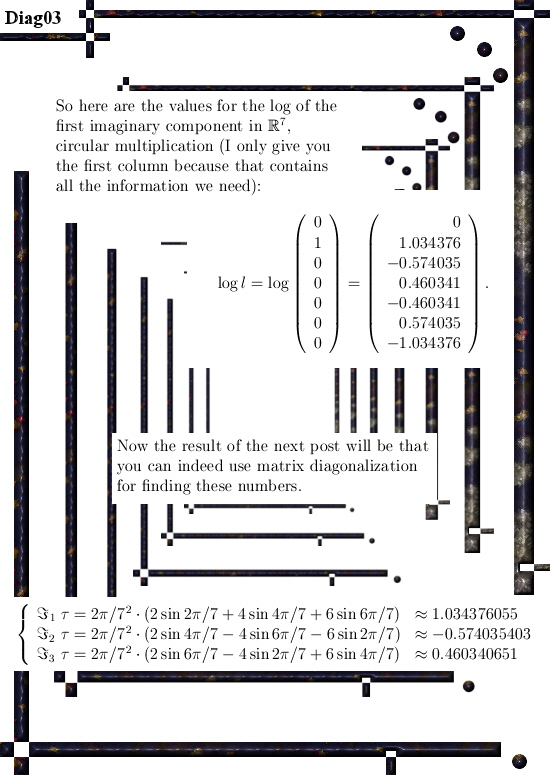
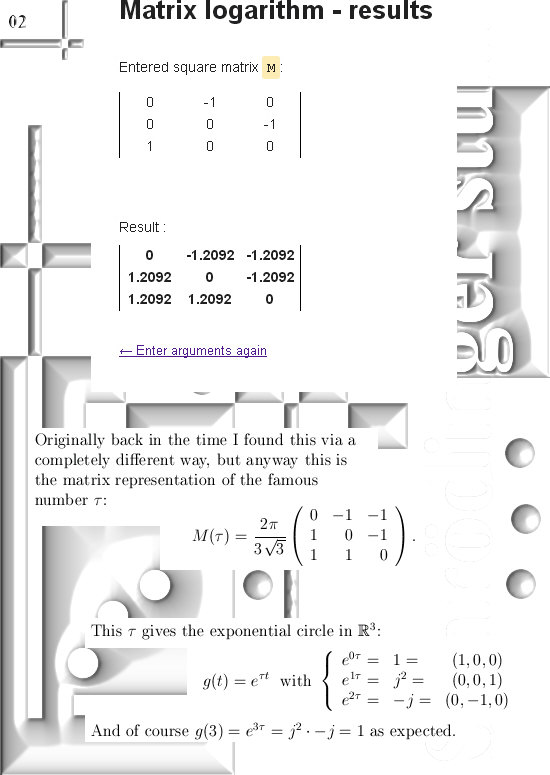
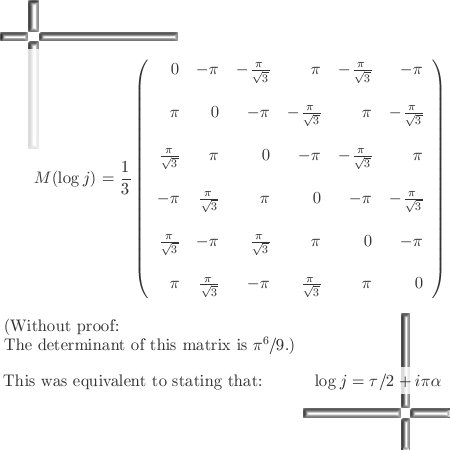
In the next three pictures I show you some screen shots with numerical values of matrix representations and the logarithm of those matrix representations.

The goal is to find mathematical expressions for the observed numerical values that are calculated via the above mentioned de Pade approximation. We don’t want only numerical approximations but also catch the stuff in a mathematical formulation.

At the end of the third picture you see the end result.

So it took some time to find this result, I wasted an entire week using the wrong cut in the complex plane. And that was stupid because I had forgotten my own idea when riding my noble iron horse through the Harener swamps…

The result for the seven dimensional number tau (circular version) as calculated in the next post is a blue print for any dimension although I will never write stuff down like in a general dimension setting because that is so boring to read.

Ok, see you around my dear reader.

On a way to find more equations so that the 1D existence of exponential curves in all possible dimensions is assured.

November 8, 20173D complex numbers, 5D complex numbers, Exponential circle, Exponential curves, Matrix representation, Quantum mechanicsReinkoVenema

In part this post picks up where I left the stuff of the missing equations back in the year 2015. The missing equations are found inside the determinant equation; for this to succeed we must factorize determinant of the matrix representations of higher dimensional numbers. A well known result from linear algebra is that the determinant is also the product of the eigen values; so we need to craft the eigen value functions that for every X in our higher dimensional number space give the eigen values.

These eigenvalue functions are also the discrete Fourier transform of our beloved higher dimensional numbers and these functions come in conjugate pairs. Such a pair form two factors of the determinant and if we multiply them we can get rid of all complex coefficients from the complex plane.

A rather surprising result is the fact that if we subtract a cone equation from a sphere equation we get a cylinder…

This post is also a way of viewing the exponential circles and curves as an intersection of all kinds of geometric objects like the unit sphere, (hyper) cones, (hyper) planes and (hyper cylinders. Usually I represent it all as some analysis but you can take a very geometric approach too.

I have no idea if the shape of the higher dimensional curves is studied as a geometrical object; I suspect this is not the case since the use of complex numbers outside the complex plane is very seldom observed. The professionals just want their tiny fishing bowl (the complex plane) and declare it an Olympic swimming pool…
Well, let it be because these people will never change.

All in all this post is 20 pictures long (size 550 x 775) so it is a relatively long read.

The pictures of the graphs were all made with an applet named Animated drawing, here is a link and there you can find it under ´Online calculators and function plotters´±

https://wims.sesamath.net/wims.cgi

For example you can cut and paste the next five dimensional equations that represents a hypercone going through all the coordinate axis:

((1/5)*sin(5*x)/sin(x))*((1/5)*sin(5*(x-2*pi/5))/sin(x-2*pi/5)) +
((1/5)*sin(5*(x-2*pi/5))/sin(x-2*pi/5))*((1/5)*sin(5*(x-4*pi/5))/sin(x-4*pi/5)) +
((1/5)*sin(5*(x-4*pi/5))/sin(x-4*pi/5))*((1/5)*sin(5*(x-pi/5))/sin(x-pi/5)) +
((1/5)*sin(5*(x-pi/5))/sin(x-pi/5))*((1/5)*sin(5*(x-3*pi/5))/sin(x-3*pi/5)) +
((1/5)*sin(5*(x-3*pi/5))/sin(x-3*pi/5))*((1/5)*sin(5*x)/sin(x))

The above thing should give identical zero for all x.
An important feature of exponential curves in spaces with an odd number of dimensions is that they all are inside a hyperplane. The hyperplane says the sum of the coordinates is always 1. If you cut and past the next sum of the five coordinate functions you see that you always get one for all x:

((1/5)*sin(5*x)/sin(x)) +
((1/5)*sin(5*(x-pi/5))/sin(x-pi/5)) +
((1/5)*sin(5*(x-2*pi/5))/sin(x-2*pi/5)) +
((1/5)*sin(5*(x-3*pi/5))/sin(x-3*pi/5)) +
((1/5)*sin(5*(x-4*pi/5))/sin(x-4*pi/5))

At last the link to the original update from 2015 where I found the missing equations for the first time. But all I knew they were hidden inside the determinant. A few weeks ago I decided to take a better look and the result is this post.

From 14 July 2015: The missing equations.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#14July2015

Ok, that is what I had to say. Till updates.

On an old idea that did not work…

November 2, 20175D complex numbers, Exponential circle, Exponential curves, Matrix representationReinkoVenema

Recently I am working on a relatively long post where I try to take a much more geometric approach to finding exponential circles and exponential curves. That post is also going forward from a few years back when I was searching for the so called missing equations.

The problem of the missing equations does not arise until you start working in five dimensions or higher; the equations as generated by the sphere-cone equations are just not enough to end up with a one dimensional curve.
Back in the time I simply took a few weeks until I had found the answer: The missing equations can be found inside the determinant!

For example if you have a 17 by 17 matrix in 17 variables (the so called matrix representations of 17-dimensional number systems), all you have to do is factorize this determinant and from those factors you can craft the extra needed equations.

Weirdly enough you find a hyper plane and a bunch of hyper-cylinders.

So in the next post I try to show you how you can have a very geometric approach to finding the higher dimensional exponential curves as the intersection of a sphere, a hyperplane, a bunch of cones and a bunch of cylinders.

__________

In my old notes I found a mysterious looking line of squares of cosines with their time lags. That was from before I solved the problem and this ‘solution’ has all kinds of faults in it.

That is this small post; it is about something that does not work.
It is just 3 pictures long (550 x 775 pixels):

It was just over two years back I wrote that long update on the other website about the missing equations, I was glad I took those weeks to solve this problem because it is crucial for the development of general higher dimensional theory on this detail.

Here is a link to that old update±

From 14 July 2015: The missing equations.

I hope next week I am ready with the new long post, after that I will likely pick up magnetism again because I finally found out what the professionals mean when talking about ´inverted V-s’; that means there is also an electric field accelerating the particles in the aurora’s of earth and Jupiter.

Tiny problem for the professionals: At the Jupiter site, regardless of inverted V-s yes or no, the plasma particles get accelerated anyway…
So that looks like one more victory for Reinko Venema and one more silence from the professional professors.

See ya around!

Some corrections and an addendum + a new way of taking Fourier transforms.

June 1, 20173D complex numbers, Corrections, Exponential circle, Exponential curvesReinkoVenema

This post has many goals, for example in the previous post I talked about a ‘very rudimentary Fourier transform’. In this post it is a bit less rudimentary, a bit more satisfying definition is given but still I did not research all kinds of stuff like the existence of an inverse & lot’s more basic stuff.

For myself speaking I consider this ‘new Fourier transform’ more as some exotic bird that, if capable to fly a few meters, will only draw applause from specialists in Fourier analysis.
So for myself speaking I am far more happy we need a more advanced number tau and the mathematical miracles you can do with it in three dimensions.

Therefore I included two examples of exponential curves that go through the plus and minus of all three basis vectors in 3D space, after all this is one of my most remarkable math results…

In this post I also show you how to use the calculus of ‘opposite points, in three dimensions it works like a bullet train but the higher the dimensions become the harder it is to frame it in simple but efficient calculus ways like using opposite points on exponential circles.

Another thing to remark is that an exponential circle is always a circle; it is flat in the 2D sense and has a fixed radius to some center. When this is not the case I always use the words exponential curve…

This post is nine pictures long, I truly hope you learn a bit from it.
You really do not need to grasp each and every detail, but it is not unwise to understand that what I name the numbers tau are higher dimensional versions of the number i from the complex plane.

Ok, here we go:

In these nine pictures I forget to remark you can also craft a new Cauchy formula for the representation of analytic functions. For myself speaking this was far more important compared to a new way of Fourier transform.

You still need that more advanced version of tau…

Can´t get enough of this stuff?
Ten more pictures dating back to 2014 at the next link:

From 18 Jan 2014: Cauchy integrals
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#18Jan2014

A link to the Nov 2016 post on 2D split complex numbers that contains the disinformation about the sum of the coordinate functions:

The second hybrid: a 4D mix of the complex and the circular plane.

End of this post, likely the next post is about prime numbers and how to demolish the internet security we think we have using huge prime numbers…

So see you around!

The second hybrid: a 4D mix of the complex and the circular plane.

November 24, 2016Exponential circle, Exponential curvesReinkoVenema

Update from 30 Nov: My health problems persist, my right wrist is still swollen and hot all the time. So after one week it is clear I need to see a doctor…
Anyway I can type text with one hand so here we go:

In this update I talk about the circular plane because I want to use the same language in 2D as in 3D or higher, yet for those living in the mud this stuff is mostly named split complex numbers. There are more names going round: for those people that do not understand what the conjugate of a number is and how to find those, they name it hyperbolic numbers.

This update is about finding the log of the first and only imaginary unit of the circular (also named split or hyperbolic) numbers. This mathematical goal can only be achieved by replacing the real scalars in the circular plane by numbers from the complex plane.
That replacement stuff is known in my household as the Sledgehammer Theorem, this theorem says you can more or less always replace scalars by higher dimensional numbers. But this has to make some sense; for example you have a number from the complex plane like z = a + bi, now if you replace the two real numbers a and b with general numbers from the complex plane you did not gain much. As a matter of fact you gained nothing at all because you are still inside the complex plane and other people will only laugh at you:

That is just like the way Donald Trump will expand the US economy…

For myself speaking I do not understand that a math result as in this post is more or less unknown to the professional math community. How can it be that Euler has all that stuff of finding the God formula while century in century out the math professors make no progress at all?

Every day I am puzzled by this because I am not ultra smart or so, it is only my emotional system is a bit different: I never get scared when hunting down some good math…

__________

Anyway from the mathematical point of view I am proud of this ten picture long update: it is as close as possible to the calculation that unearthed the very first exponential circle. That was the discovery that in the complex plane the log of i is given by i pi over 2.

Need a cold shower by now?

Want to restore your faith in the old masters with their superior use of math?

Try the next video from the Youtube channel, it only uses insights from the circular plane and he runs fast and far: The Lorentz boost inside special relativity:

Split complex numbers and the Lorentz boost.

Let’s leave this update with that, have a good life or try to get one.

Update from 04 Dec 2016: I would like to post the number one wiki when you do an internet search of split complex numbers. (There are all kinds of names going round, but the circular plane is also the split complex number plane for sure.)
As usual all that stuff has the conjugate wrong, but in the next wiki you see more or less the combined wisdom of the math community when it comes to expanding the complex plane to higher dimensions. (It is a dry desert, human brains are not that fit for doing math):

Split-complex number.
https://en.wikipedia.org/wiki/Split-complex_number

Once more: those people have got it wrong about how to find the conjugate and as such you can also find lots of pdf files about circular (or split-complex) numbers that say they are hyperbolic numbers.
The common fault is that they use the conjugate just as if you conjugate an ordinary complex number from the complex plane.

I remember I did that too for a couple of years until it dawned on me that we are only looking at the projections of the determinant; it has nothing to do with lengths, even in the complex plane it is not the norm of the complex number but it’s matrix representation and the determinant.

All stuff you find on this on the internet is nothing but shallow thinking.

End of this update, see yah in the next post.

How I found the first modified Dirichlet kernel in 5D numbers.

July 7, 20163D complex numbers, 5D complex numbers, Exponential circle, Exponential curves, Matrix representation, Quantum mechanicsReinkoVenema

Back in Jan 2014 I was able to solve the circular and complex 5D numbers systems using the so called ‘tau-calculus’. Basically tau-calculus is very easy to understand:

Find a basis vector (from an imaginary number) that has determinant +1.
Craft analytical expressions that you cannot solve but use internet applets for numerical answers. Or, equivalent:
Use an applet to calculate the logarithm of your basis vector once you have put it on a matrix representation.
Start thinking long and hard until you have solved the math analysis…

This is easy to understand but I could only do this in three and five dimensional space, seven or eleven dimensional space? It is now 2.5 years later and I still have no clue whatsoever.

Anyway back in the time it was a great victory to find the exponential curves in 5D space. May be some people with insect like minds think that the Euler identity is the greatest formula ever found but let me tell you:
The more of those exponential circles and curves you find, the more boring the complex plane becomes…

In the months after Jan 2014 I wanted to understand the behavior of the coordinate functions that come along those two exponential curves. But the problem kept elusive until I realized I had one more round of internet applets waiting for me.
I had to feed this internet applet for the log of a matrix over 50 matrices and write down the answers it gave me; that was a lot of work because every matrix had 25 entries.

Originally I planned for ‘digesting’ 10 matrices a day so it would be a five day project, but when I finally started somewhere in June 2014 after two days I was ready to sketch my strongly desired coordinate function of the very first coordinate in 5D space.

I still remember sitting at my table and do the drawing and when finished it was so fast that I realized the next: This is a Dirichlet kernel.

And the way I used it, it was so more simple to write down this kernel and if you think how those exponential curves in higher dimensional spaces work with their starting coordinate function and all the time lags that follow… This finding will forever be in the top ten of most perfect math found by your writer Reinko Venema…

__________

Ok, what is in this new post?
Nine pictures of size 550 x 775 pixels containing:
Basic definitions upon 5D complex and circular number &
Tau calculus for the exponential curve &
Explaining how I found the graph of the first modified Dirichlet kernel &
A small quantum physics example related to probability amplitudes &
Some cute integrals that are easy to crack now.

Hope you can learn a bit from it, do not worry if you do not understand all details because even compared to the 2D complex plane or the 3D complex numbers this website is about:
The 5D realm is a space on it’s own!

Have fun reading & thinking upon it:

A few links of interest are the next:

You need a good applet for the log of a matrix representation if you want, for example, crack the open problem in tau calculus for the 7D complex numbers:
http://calculator.vhex.net/calculator/linear-algebra/matrix-logarithm

My original update on the other website about the 5D number systems from Jan 2014:
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#30Jan2014

If you are more interested in those kind of weird looking integrals suddenly easy to solve if you use a proper combination of geometry and analysis, the update from July 2015 upon the missing equations is also worth a visit:
The missing equations.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#14July2015

__________

This is what I more or less had to say, have a nice life or try to get one.
See you in the next post.

Modified Dirichlet kernels for low dimensions.

June 20, 20163D complex numbers, 5D complex numbers, Exponential circle, Exponential curvesReinkoVenema

What the hydrogen bomb is in the average nuclear arsenal, that is what modified Dirichlet kernels are for higher dimensional complex & circular number systems.
Via the so called tau calculus I was able to achieve results in 3 and 5 dimensional number systems and I really had no hope in making more progress in that way because it gets so extremely hardcore that all hope was lost.

Yet about two years ago I discovered a very neat, clean and very beautiful formula that is strongly related to the Dirichlet kernel known from Fourier analysis. The formula I found was a dressed down version of the original Dirichlet kernel therefore I named it ‘modified Dirichlet kernel’.

This modified kernel is your basic coordinate function, depending on the dimension of the space you are working in you make some time lags and voila: There is your parametrization of your higher dimensional exponential (periodic) curve (only in 2D and 3D space it is a circle).

For myself speaking: this result of finding the modified Dirichlet kernel is for sure in my own top 10 list of most important results found. Not often do I mention other mathematicians, but I would like to mention the name of Floris Takens and without knowing how Floris thought about taking a sample of a time series and after that craft time lags on that, rather likely I would not have found this suburb and very beautiful math…

__________

I haven’t decided what the next post will be about.
It could be stuff like:

How I found the first modified Dirichlet kernel, or
Wirtinger derivatives for 3D number systems, or
Wow man, can you factorize the Laplacian operator form Quantum Mechanics???

But factoring the Laplacian requires understanding 3D Wirtinger derivatives so likely I will show you how I found the very first modified Dirichlet kernel.

__________

This update contains six jpg pictures each about 550 x 775 pixels and two old fashioned animated gif pictures. I tried to keep the math as simple as possible and by doing that I learned some nice lessons myself… Here we go:

This is the animated gif using z = 0 in 3D while this picture is showing the Euler exponential circle:

Here is an animated gif of how this coordinate function looks when you combine it with the two time lags for the y(t) and z(t) coordinates. Does it surprise you that you get a flat circle?
If it does not surprise you, you do not understand how much math is missing in our human world…

In case you are interested in the ‘time lag’ idea as Floris used it, here is a nice Youtube video that gives a perfect explanation. If you apply this time lag idea for example is a 17 dimensional real vector space you get a 17D exponential curve with all of it’s magnificent properties…

Takens’ theorem in action for the Lorenz chaotic attractor

Yes, end of this post. See ya around & have a nice life or try to get one.

Third post on the Schrödinger wave equation using 3D complex numbers for atomic & molecular orbitals.

April 13, 20163D complex numbers, Exponential circle, Exponential curves, Matrix representation, Quantum mechanicsReinkoVenema

This update is 10 pictures long, the pictures are sized 550 by 775 pixels.
This update covers more or less everything, but I still have to explain how you find the six coordinate functions the poeple will need in order to see if these kind of complex numbers give the same result as ordinary complex numbers from the complex plane.

For those that cannot wait: In the post from 03 April I posted a teaser picture with the coordinate functions in 3D, if you multiply this against the e to the power i pi alpha thing in this update you have the six coordinate functions…

Ok ok you neatly have to write them out, but basically it is all there.

At first I was thinking it would be hard to get different results using these higher dimensional complex numbers, but when talking about atomic and molecular orbitals it might be more subtle than it looks. At the end I will post a video where some physics guy shows all kinds of orbitals related to hydrogen but his stuff is different from the pictures we observe in chemistry.
He explains this by saying that the people from chemistry always take a super-position of two wave-blobs and as such it gets oriented along the y-axis say.
If you would take super-positions of my 3D complex numbers you will get very similar results. look at the drawing in the one before last picture:
Take a super-position of an exponential circle and it’s conjugate and observe it must have the same behavior as 2D numbers from the complex plane.

(In that drawing your eys is supposed to be along the line through zero and alpha, so zero is right behind the center of the shown circle…)

Enough of the bla bla bla, here are the 10 pictures:

Click on the picture to get a larger version of the drawing:

Now finding these atomic & molecular orbitals is very hard, for simple atoms like hydrogen it is doable but what about uranium or some nice protein with only 3693 atoms in it?

All that kind of stuff falls under what we name n-body problems and for n above 3 it seems impossible to find exact analytical solutions.

There is a nice video out there explaining a bit more on the topic of finding the shapes of atomic & molecular orbitals. It is from Brant Carlson and has the title Hydrogen atom wavefunctions:

Ok, that was it for today. Till updates.

Some good math for the physics community.

April 3, 20163D complex numbers, Exponential circle, Exponential curves, Quantum mechanicsReinkoVenema

Ok ok I made a relatively big blunder when sending the people from quantum mechanics using the Schödinger equation into the direction of the 3D complex numbers.

Because as a matter of fact, you cannot solve the factual Schrödinger equation in the 3D complex number system because there is no famous i to be found with the property that i^2 = -1.

You need a more advanced number system and I will explain that in detail in an upcoming post number three on the Schrödinger wave equation.

__________

In the meantime, it has not fallen on deaf ears on my side that after I posted the first Schrödinger post and I later did an internet search, suddenly with the search phrase ‘3Dcomplexnumbers’ I suddenly ended on number 1, 2 and 3.
So like expected it drew a lot of attention.

Therefore I would like to give a kind of present to the physical community because also not fallen on deaf ears, as far as I observe it physics people always try to use a product integral when they can.

Product integrals were my first serious mathematical invention, I found them while I was still trying to get my first year exam al the local university. Math professors almost never use product integrals because they are to stupid for that but physics people often put it in product integral representation.

How the history of that detail is I do not know, may be Paul Dirac had a bit to do with it…

Anyway, some time ago I wrote a pdf with the title

A tribute to Euler. Title: Ten styles for product integrals and product differentiation.
http://kinkytshirts.nl/pdfs/Product_integrals.pdf

__________

So far for the gift or the present, if you want to use other number systems beside the complex plane for depicting atomic orbitals or whatever you want to do with it, you also must know more about exponential circles and curves.

Physics people use so called ‘phase shift’ all of the time, but that is only multiplying some stuff with e to the power it or so. This is the sandpit exponential curve for toddlers.

In the world of the grown ups we have all kinds of other exponential circles and curves and guess what? I have a pdf for you with another 10 pieces of exponential circles & curves:

An overview of exponential circles and curves.
http://kinkytshirts.nl/pdfs/10_exponential_circles_and_curves.pdf

A possible way of parametrization of 3D exponential circles is given in the next picture and understanding this stuff is important when it comes to the third post related to the Schrödinger equation:

This is the end of this intro to the third Schrödinger post.
Have a nice life or try to get one.

Till updates.

A new type of Cauchy integral formula.

February 28, 20163D complex numbers, Exponential circle, Exponential curves, Matrix representationReinkoVenema

Yesterday I wrote a new post on the Schrödinger equation using 3D complex numbers but before I post that let’s go a bit more hardcore with a brand new Cauchy integral formula.
Actually it is not that brand new because on 18 Jan 2014 I posted it on the other website.

Now in a normal world a brand new Cauchy integral would be greeted with a lot of joy and plenty of discussion, yet that has not happened by now. Once more we observe that among professional math professors there is a severe problem concerning the so called ‘competence question’.
Or may be it is better to frame this into a lack of competence; if you have that you are also not able to judge new results properly and this is what we observe year in year out.

But I have to admit it is a relatively hardcore update, it is 10 pages long and I remember clearly it was fun to write because I wanted to prove the Cauchy formula in this way for a long time.

Source: http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#18Jan2014

__________

Now a person that is not 100% insane might wonder how the hell you calculate the determinant of a six by six matrix because in parctice that is an awful amount of work. But I used an internet applet and as such got a numerical value like about 106,821 and within a few seconds I recognized this as being pi to the power of six divided by nine.

Once back in the year 1992 I came across that number and it was kinda weird to observe that in 2014 it was still floating around in my brain. Sometimes I wonder if I am the crazy one and the math professors are the ones with healthy brains…;)

Ok, till updates my dear reader.