Category Archives: Matrix representation

Part 17: The inverse of a 4D complex number old school style (via minor matrices).

December 7, 20184D complex numbers, Matrix representationReinkoVenema

Ha, a couple of weeks back I met an old colleague and it was nice to see him. We made a bit of small talk and more or less all of a sudden he said: ‘But you still can always do this’. And he meant getting a PhD in math.

I was a bit surprised he did bring this up, for me that was a station passed long ago. But he made me thinking a bit, why am I not interested in getting a math degree?

And when I thought it out I also had to laugh: Those people cannot go beyond the complex plane for let’s say 250 years. And the only people I know of that have studied complex numbers beyond the complex plane are all non-math people. Furthermore inside math there is that cultural thing that more or less says that if you try to find complex numbers beyond the complex plane, you must have a ‘mental thing’ because have you never heard of the 2-4-8 theorem?

Beside this, if I tried it in the years 1990 and 1991 with very simple: Here this is how the 3D Cauchy Riemann equations look… And you look them in the eyes, but there is nothing happening behind those eyes or in the brain of that particular math professor. Why the hell should I return and under the perfect guidance of such a person get a PhD?

I am not a masochist. If complex numbers beyond the complex plane are ignored, why try to change this? After all this is a free world and most societies run best when people can do what they are good at. Apparently math like I make simply falls off the radar screen, I do not have much problems with that.

___________

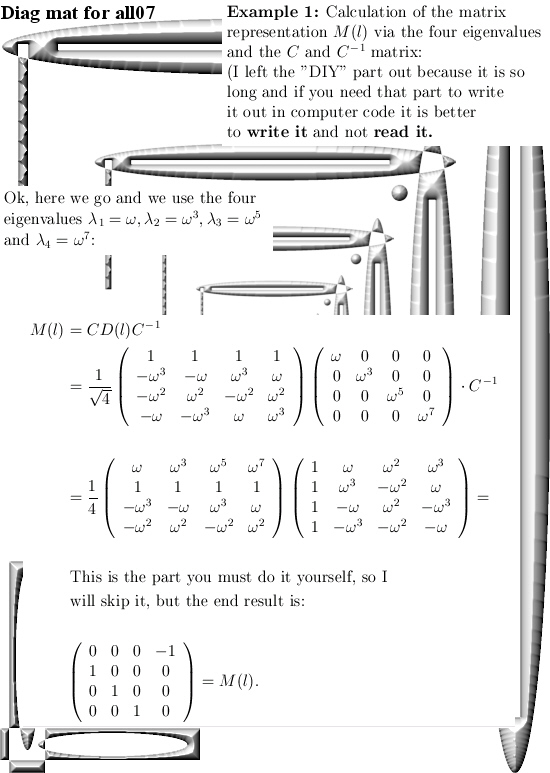
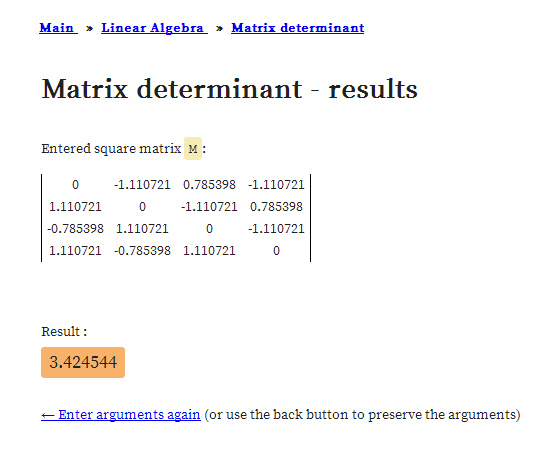
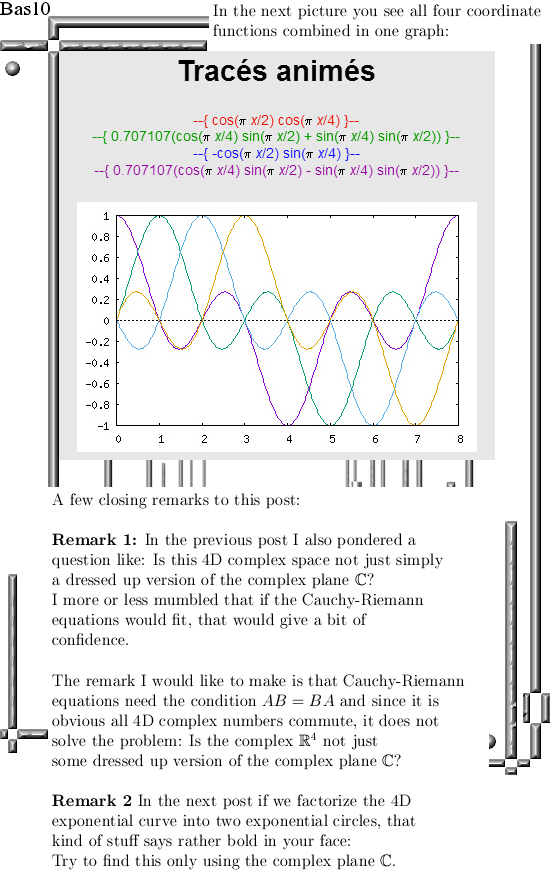
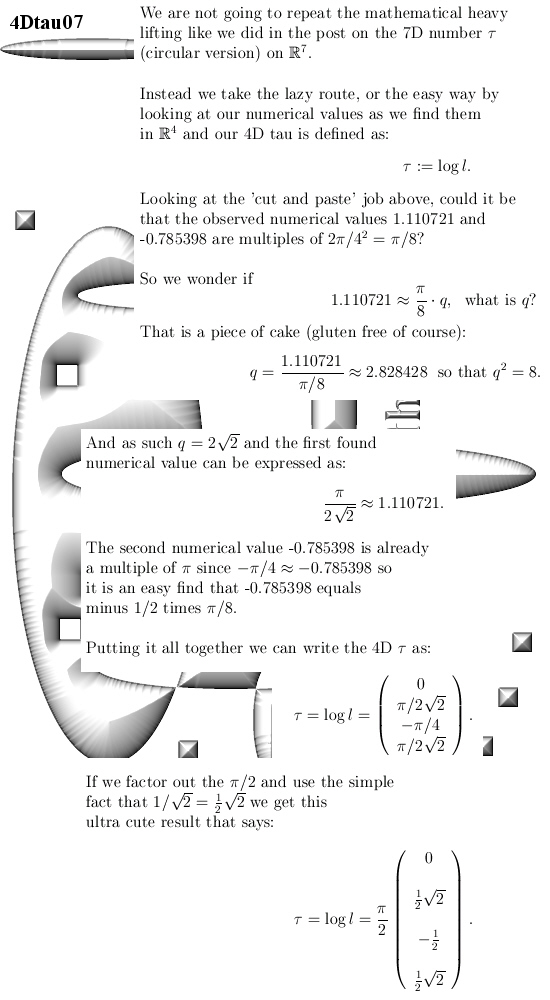
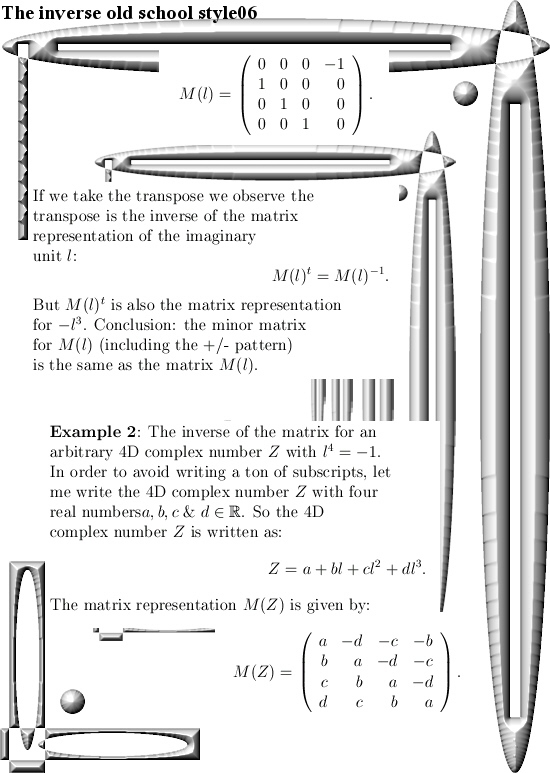
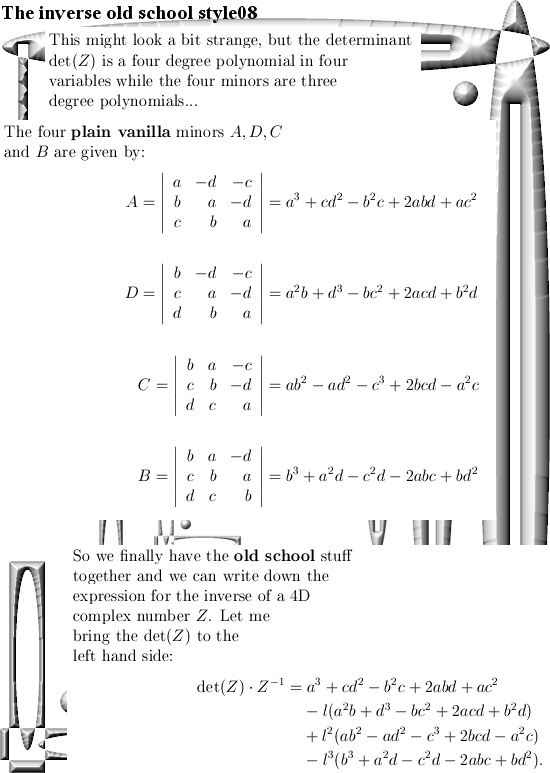
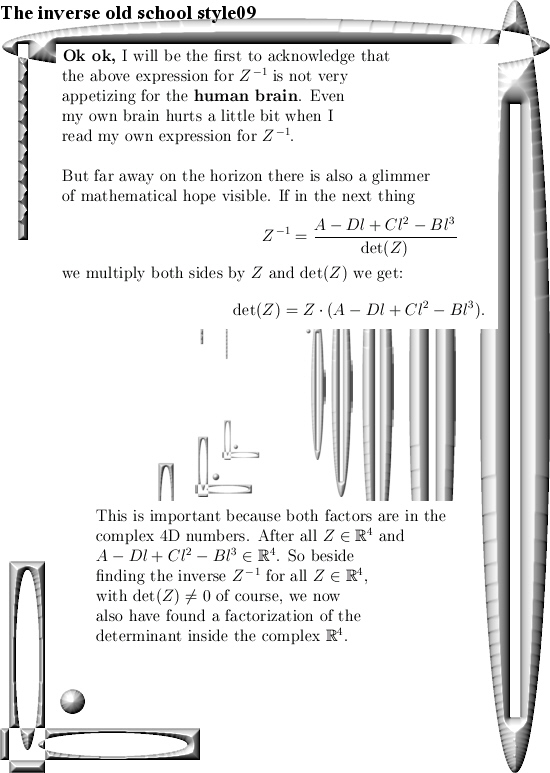
After having said that, this update Part 17 in the basics to the 4D complex numbers is as boring as possible. Just finding the inverse of a matrix just like in linear algebra with the method of minor matrices.

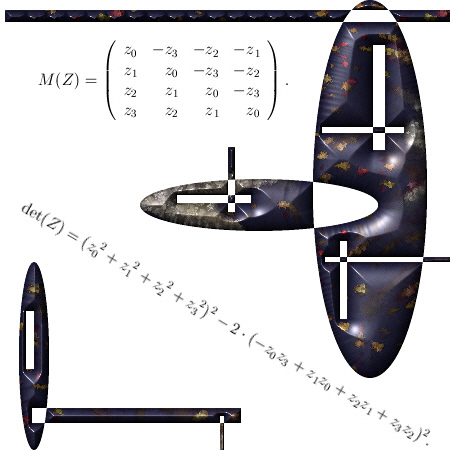
Believe me it is boring as hell. And after all that boring stuff only one small glimmer of light via crafting a very simple factorization of the determinant inside the 4D complex numbers. So that is very different from the previous factorization where we multiplied the four eigenvalue functions. From the math point it is a shallow result because it is so easy to find but when before your very own eyes you see the determinant arising from those calculations, it is just beautiful. And may be we should be striving a tiny bit more upon mathematical beauty…

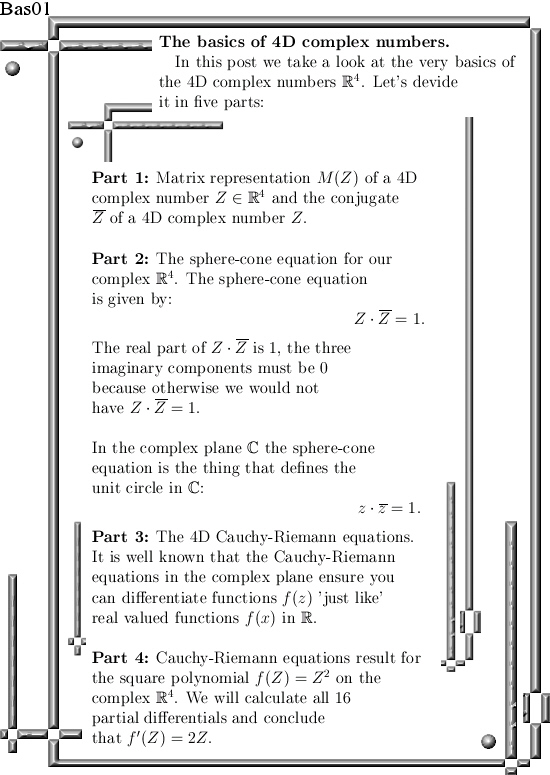
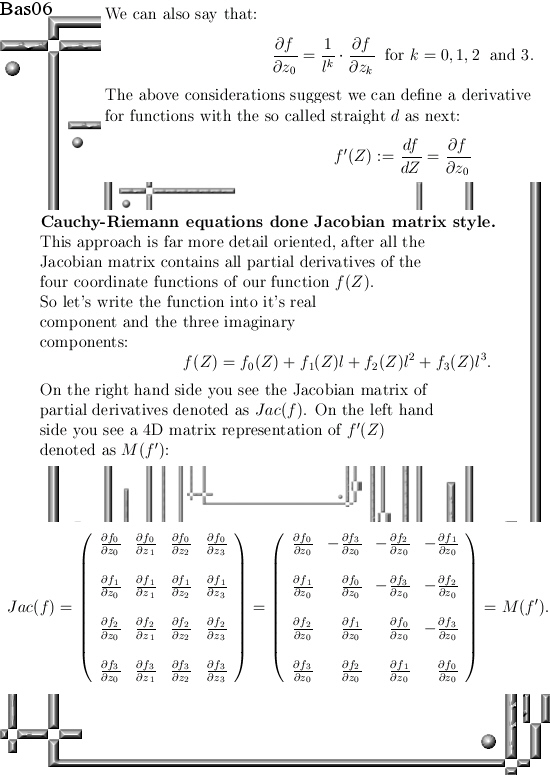
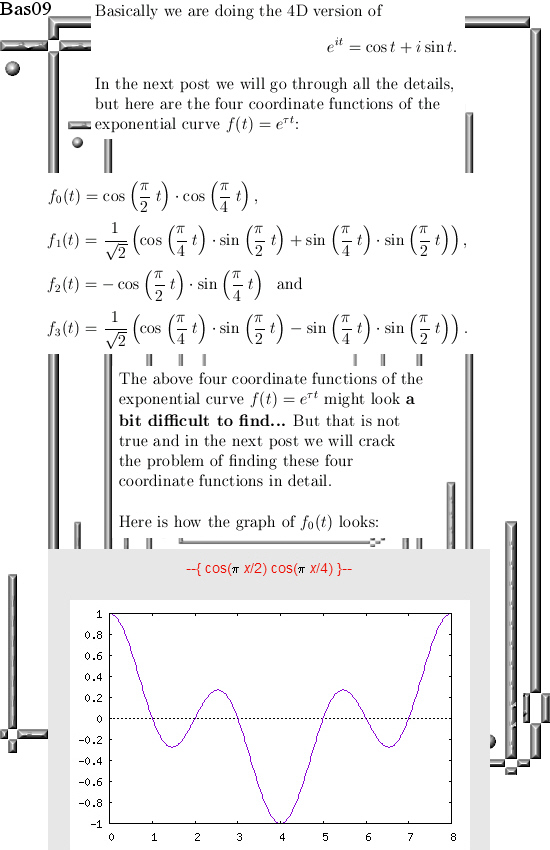
This post is nine pictures long in the usual size of 550×775 pixels.

As an antidote against so much polynomials like det(Z), with 2 dimensions like a flatscreen television, you can do a lot of fun too. The antidote is a video from the standupmaths guy, it is very funny and has the title ‘Infinite DVD unboxing video: Festival of the Spoken Nerd’. Here is the vid:

End of this update, see you around.

Ok ok, a few days later I decided to write a small appendix to this post and in order too keep it simple let’s calculate the determinant of the 3D circular numbers. I have to admit this is shallow math but despite being shallow it gives a crazy way to calculate the determinant of a 3D circular number…

So a small appendix, here it is:

And now you are really at the end of this post.

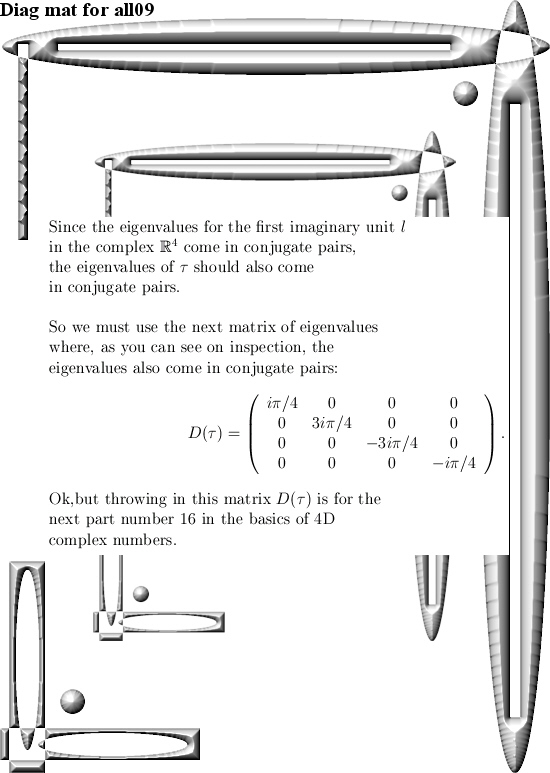
In the next post let’s calculate the inverse of the 4D complex tau number. After all a few months back I gave you the new Cauchy integral representation and I only showed that the determinant of tau was nonzero.

But the fact that the Cauchy integral representation is so easy to craft on the 4D complex numbers arises from the fact the inverse of tau exists in the first place. In 3D the number tau is not invertible, and Cauchy integral representations are much more harder to find.

Ok, drink a green tea or pop up a fresh pint, till updates.

Calculation of the 4D number tau diagonal matrix style.

November 12, 20184D complex numbers, Exponential curves, Matrix representationReinkoVenema

In the begin of this series on basic and elementary calculations you can do with 4D complex numbers we already found what the number tau is. We used stuff like the pull back map… But you can do it also with the method from the previous post about how to find the matrix representation for any 4D complex number Z given the eigenvalues.

Finding the correct eigenvalues for tau is rather subtle, you must respect the behavior of the logarithm function in higher dimensions. It is not as easy as on the real line where you simply have log ab = log a + log b for positive reals a and b.

But let me keep this post short and stop all the blah blah.

Just two nice pictures is all to do the calculation of the 4D complex number tau:

(Oops, two days later I repaired a silly typo where I did forget one minus sign. It was just a dumb typo that likely did not lead to much confusion. So I will not take it in the ‘Corrections’ categorie on this website that I use for more or less more significant repairs…)

Ok, that was it.

Diagonal matrices for all 4D complex numbers.

November 8, 20184D complex numbers, Exponential curves, Matrix representationReinkoVenema

This website is now about 3 years old, the first post was on 14 Nov 2015 and today I hang in with post number 100. That is a nice round number and this post is part 15 in the series known as the Basics for 4D complex numbers.

We are going to diagonalize all those matrix representations M(Z) we have for all 4D complex numbers Z. As a reader you are supposed to know what diagonalization of a matrix actually is, that is in most linear algebra courses so it is widely spread knowledge in the population.

Now at the end of this nine pictures long post you can find how you can calculate the matrix representation for M(l) where l is the first imaginary unit in the 4D complex number system. And I understand that people will ask full of bewilderment, why do this in such a difficult way? That is a good question, but look a bit of the first parts where I gave some examples about how to calculate the number tau that was defined as log l. And one way of doing that was using the pull back map but with matrix diagonalization you have a general method that works in all dimensions.

Beside that this is an all inclusive approach when it comes to the dimension, in practice you can rely on internet applets that use commonly known linear algebra. Now if you are a computer programmer you can automate the process of diagonalization of a matrix. I am very bad in writing computer programs, but if you can write code in an environment where you can do symbolic calculus in your code, it would be handy if that is on such a level you can use the so called roots of unity from the complex plane. After all the eigenvalues you encounter in the 4D complex number system are always based on these roots of unity and the eigenvectors are too…

This post number 100 is 9 pictures long, as usual picture size is 550 x 775 pixels.
In the next post number 101 we will use this method to calculate the matrix representation of the number tau (that is the log of the first imaginary unit l).

Ok, here are the pictures:

That´s it, in the next post we go further with the number tau and from the eigenvalues of tau calculate the matrix representation. So see you around.

Part 14: The Cauchy integral representation for the 4D complex numbers.

October 11, 20184D complex numbers, Exponential circle, Exponential curves, Matrix representationReinkoVenema

It took me longer than expected to craft this update. That is also the nature of the subject; you can view and do math with Cauchy integral representation in many ways. In the end I settled on doing it just for polynomials of finite degree and even more simple: these polynomials are real valued on the real line. (So they have only real coefficients and after that are extended to the space of 4D complex numbers).

In another development, last week we had the yearly circus of Noble prizes and definitely the most cute thing ever was those evolving protein molecules. Because if you can use stuff like the e-coli bacteria you can indeed try if you can (forcefully) evolve the proteins they make… That was like WOW. Later I observed an interview with that chemistry Nobel prize winner and she stated that when she began she was told ‘gentlemen don’t do this kind of thing’.

So she neglected that ‘gentlemen stuff’ and just went on with it. That is a wise thing because if you only do what all those middle age men tell you to do you will find yourself in the very same hole as they are in…
The physics prize was also interesting, for myself speaking I was glad we did not observe those physics men totally not understanding electron spin but with the usual flair of total arrogance keep on talking about spin up and spin down.

You can also turn that spin nonsense upside down: If elementary particles only carry monopole electrical charge than why should electrons be bipolar when it comes to magnetism? That Gauss law of magnetism is only a thing for macroscopic things, there is no experimental proof it holds for quantum particles…

But let’s talk math because this update is not about what I think of electron spin. This is the second Cauchy integral representation I crafted in my life. Now the last years I produced a whole lot of math, my main file is now about 600 pages long. But only that very first Cauchy integral representation is something that I printed out on a beautiful glossy paper of size A0. That first Cauchy integral representation was on the space of 3D numbers and there life is hard: The number tau has determinant zero and as such it is not invertible. But I was able to complexify the 3D circular numbers and it was stunning to understand the number tau in that complexification of the 3D circular numbers. Just stunning…

Therefore I took so much time in trying to find an easy class of functions on the space of 4D complex numbers. I settled for easy to understand polynomials, after all any polynomial gives the same value everywhere if you write them as a Taylor series.
Since this property of polynomials is widely spread I can safely say this in this part 14 of the basics to the 4D complex numbers we have the next Theorem:
THEOREM: The math will do the talking.
PROOF: Just read the next 12 pictures. QED.

As usual all pictures are 550 x 775 pixels in size. I also use a thing I name ‘the heart of the Cauchy integral’, that is not a widely known thing so take your time so that the mathematical parts of your brain can digest it…

I truly hope the math in this update was shallow enough so you can use it in your own path of the math that you like to explore.

End of this post, may be in Part 15 we will finally do a bit more about the diagonalization of 4D complex numbers because that is also a universal way of finding those numbers tau in the different dimensions like the 17D circular numbers & all those other spaces.

Have a nice life or try to get one.

Part 13 of the basics of 4D complex numbers: Factorization of the determinant.

September 12, 20184D complex numbers, Matrix representationReinkoVenema

It is about high time for a small update. Originally I wanted to include a little rant against all those math professors that have stated that the so called Euler formulae for the exponential circle in the complex plane is the most beautiful piece of math ever.

How can you say that and after all those other exponential circles and curves I found stay silent year in year out? We now have a fresh academic year and likely the new year nothing will happen again.

The same goes for magnetism, if it is true electrons carry magnetic charge one way or the other this will have huge economical impacts in the long run. Not only can you better understand how spintronic devices can work but as a negative also understand how nuclear fusion with those Tokomak things will never work because of the electron acceleration.

In my view this is important given the speed of climate change and how slow we react on it while at the same time we are always promised golden mountains of almost free energy if only we had nuclear fusion…

But likely university people are university people so we will just observe one more academic year of just nothing.

__________

After having said that, in this post we calculate the determinant via multiplying the four eigenvalues every 4D complex number Z has. Of course that is always when such a Z is viewed as it’s matrix representation M(Z).

You can do much more with that kind of stuff, in the previous part number 12 we unearthed the eigenvalues and eigenvectors so we can also do the nice thing of matrix diagonalization. I have not planned anything about the content in the next few parts of these small series on 4D complex numbers. So we’ll see.

This post is five pictures long, at the end I also show you the so called cylinder equation from 3D space (circular version).

Have fun reading it and thinking about it a little bit. See you around.

Before the actual post I will show you the teaser picture as published on the other website, it contains the matrix who’s determinant we are going to factor. When I read all these posts on 4D complex numbers backwards it was only in the basics number 3 where I mentioned this explicit matrix representation M(Z).

In the teaser picture you also see the main result. I never worked out the determinant of the matrix M(Z) via a method like expansion via the minors or so. Just going straightforward for the eigenvalue functions and multiply these in order to get the determinant for any 4D complex number Z.

So it is the determinant of the matrix representation M(Z) we are going to factorize.
Here we go:

Ok, let´s not rant because why waste all that emotional energy on university people?
But it is now almost your years back since I crafted a pdf about the first 10 exponential circles and curves I found:

An overview of exponential circles and curves in …
http://kinkytshirts.nl/pdfs/10_exponential_circles_and_curves.pdf

That was from 22 December 2014. We can safely conclude that at most universities a lot is happening, but it is mostly weird stuff. Weird stuff like ‘The sum of all integers equals minus 1/12…’ Oh oh, if you have people like that inside your ranks how can that bring any good?

So is it science or comedy in the next video?

It is more like comedy I just guess…

But what would life be without comedy? That would also be a strange place to live, a life without observable comedians likely is a less funny place to live in.

Hey let’s pop open one more pint of beer. By the way in the quantum world every thing is different and at first I could not believe that, why would that be? It was years and years later I found out that quantum particles like electrons never drink beer. Just never. And at that point in time I finally understood just how different the quantum world is compared to our human world.

Till updates.

Part 12 of the 4D complex numbers: The four eigenvalue functions for a arbitrary 4D complex number.

September 4, 20184D complex numbers, Matrix representationReinkoVenema

In Part 11 we found the eigenvalues and eigenvectors of the first imaginary unit l (with of course the property l^4 = -1). But if we have those eigenvalues for l,it is easy to find the eigenvectors of powers of l.

But every 4D complex number is a sum of a real part and the three imaginary parts with the units l, l ^2 and l ^3. So from a linear algebra point of view it is also easy to find the eigenvalues of such combinations of l. Needless to say that in this post you should read l and it powers mostly as it’s matrix representation M(l).

I have to admit that I very often avoid the constant need for the matrix representation, for example I mostly write det(l) for the determinant of M(l). But it makes texts just so unreadable if you constant write det(M(l)), I do not like that.

When you understand how to calculate the eigenvalue functions as shown below, please remark it looks a like the so called discrete Fourier transform.

This post is five pictures long (each 550×775 pixels) although the last picture is rather empty… And why no an empty picture? After all when you had a paper book in the good old days, there were always empty pages in it. Sometimes it was even written that ‘This page is left empty intentionally’. And in those long lost years that was the crime of the century because if you write on a page that it is empty, that is never true…

In the next post we will take a look at the missing equation we still have when it comes to the calculation of the 4D exponential curve when it comes to the sphere/cone equation. we missed one equation to arrive at a 1D solution for our exponential curve.

If you also include the demand that the determinant of the exponential curve is 1 all of the time, you can squeeze out more equations inside the 4D complex numbers.

Before we say goodbye, here is a link to the matrix representation of the discrete Fourier transform. But take you time when thinking about matrices like in the link or the Omega matrix as above.

DFT matrix
https://en.wikipedia.org/wiki/DFT_matrix

Ok, that was it. Till updates.

Part 11 of the 4D complex numbers: The eigenvalues and eigenvectors from the first imaginary unit.

August 30, 20184D complex numbers, Magnetism, Matrix representationReinkoVenema

First a short magnetic update:

In reason 66 as why electrons cannot be magnetic dipoles I tried to find a lower bound for the sideway acceleration the electrons have in the simple television experiment.

To put it simple: How much sideway acceleration must the electrons have to explain the dark spots on the screen where no electrons land?

The answer is amazing at first sight: about 2.5 times 10^15 m/sec^2.
This acceleration lasts only at most two nano seconds and in the end the minimum sideway speed is about 5000 km/sec so while the acceleration is such a giant number it does not break relativity rules or so…
Here is the link:

16 Aug 2018: Reason 66: Side-way electron acceleration as in the television experiment.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff03.htm#16Aug2018

You know I took all kinds of assurances that it is only a lower bound on the actual acceleration that takes place. For example I took the maximal sideway distance as only 0.5 cm. Here is a photo that shows a far bigger black spot where no electrons land, so the actual sideway distance if definitely more than 0.5 cm.

__________

The math part of this post is not extremely thick in the sense you can find the results for yourself with the applet as shown below. Or by pencil & paper find some 4D eigenvalues and the corresponding eigenvectors for yourself.

But we need them in order to craft the so called eigenvalue functions and also for the diagonal matrices that come along with all of the matrix representations of the 4D complex numbers Z.

I hope I wrote it down pretty straightforward, this post is five pictures long. And if you like these kind of mathematical little puzzles: Try, given one of the eigenvalues like omega or omega^3, find such an eigenvector for yourself. It is really cute to write them down, multiply them by the eigenvalue and observe with your own eyes that indeed we have all that rotation over the dimensions included that omega^4 = -1 behavior.

This post is five pictures long, it is all rather basic I hope.

The applet used is from the WIMS server (https://wims.sesamath.net/), look for the Matrix calculator in the section on Online calculators and plotters.

For the time being I think that in Part 12 we will craft the eigenvalue functions for any 4D complex number Z. Ok, that was it for this update.

On a possible model for solar loops: rotating plasma.

July 30, 20184D complex numbers, Magnetism, Matrix representationReinkoVenema

Yes that is all there is: spinning plasma… At the end of last year’s summer I had figured out that if indeed electrons have far more acceleration compared to the protons, if on the sun the solar plasma starts rotating this caused a lot of electrons flying out and as such the spinning plasma would always be electrically positive.

But at the time I had no clue whatsoever about why there would be spinning plasma at the surface of the sun but lately I found the perfect culprit: The sun spins much faster at the equator compared to the polar regions.

This spinning plasma is visible at the surface of the sun as the famous sun spots and it is known these sun spots are places of strong magnetic fields.

There is a bit of a weak spot in my simple model that says all spinning plasma creates a strong magnetic field because if the solar spots are at there minimum none of them are observed for a relatively long time. The weak spot is: Why would there be no tornado like structures be made during this minimum of solar spots? After all the speed difference is still there between the equator regions and the polar regions.

Anyway the good thing is that my simple model is very falsifiable: If you can find only one spinning tube-shaped or tornado-shaped plasma structure that not makes magnetic fields, the simple model can be thrown into the garbage bin.

The simple model is found in Reason number 65 as why electrons cannot be magnetic dipoles on the other website:

Reason 65: A possible model for solar loops going between two solar spots.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff03.htm#22July2018

The main feature of the solar loops is that before your very own eyes you see all that solar plasma accelerating while according to the standard model of physics this is not possible.

Now there are plenty of physics professors stating that electrons can be accelerated by a magnetic field but if you hear them saying that you know they have never done the calculations that make it at least plausible that non constant magnetic fields are the main driver of electron acceleration.

Here are two nice pictures of what I am trying to explain with my simple model.

The above picture is in the UV part of the spectrum.

After having said that, the next post is like planned about numerical evaluations related to the four coordinate functions of the new found exponential curve f(t) for the 4D complex numbers. I hope to finish it later this week.

Now we are talking about cute numerical results anyway, in the next picture you can see numerical validation that the number tau in the 4D complex space is invertible because the determinant of it’s matrix representation is clearly non-zero.

You might say ‘so what?’. But if the number tau is invertible on the 4D complex numbers (just like the complex plane i has an inverse) in that case you can also craft a new Cauchy integral representation for that!

Again you might say ‘so what?’. But Cauchy integral representation is highly magical inside complex analysis related to the complex plane. There is a wiki upon it but the main result is a bit hard to swallow if you see it for the first time, furthermore the proof given is completely horrible let alone the bullshit after that. Anyway here it is, proud 21-century math wiki style:

Cauchy’s integral formula
https://en.wikipedia.org/wiki/Cauchy%27s_integral_formula

Ok, let’s leave it with that. Till updates my dear reader.

The basics of 4D complex numbers.

May 10, 20184D complex numbers, CR equations, Exponential curves, Matrix representationReinkoVenema

In the previous post on 4D complex numbers I went a little bit philosophical with asking if these form of crafting a 4D number system is not some advanced way of fooling yourself because your new 4D thing is just a complex plane in disguise…

And I said let’s first craft the Cauchy-Riemann equations for the 4D complex numbers, that might bring a little bit more courage and making us a little bit less hesitant against accepting the 4D complex numbers.

In this post we also do the CR equations and indeed they say that for functions like f(Z) = Z^2 you can find a derivative f'(Z) = 2Z. So from the viewpoint of differentiation and integration we are in a far better spot compared to the four dimensional quaternions from Hamilton. But the fact that the CR equations can be crafted is because the 4D complex numbers commute, that is XY = YX. And on the quaternions you cannot differentiate properly because they do not commute.

So crafting Cauchy-Riemann equations can be done, but it does not solve the problem of may be you are fooling yourself in a complicated manner. Therefore I also included the four coordinate functions of the exponential 4D curve that we looked at in the previous post.

All math loving folks are invited to find the four coordinate functions for themselves, in the next post we will go through all details. And once you understand the details that say the 4D exponential curve is just a product of two exponential circles as found inside our 4D complex numbers, that will convince you much much more about the existence of our freshly unearthed 4D complex numbers.

Of course the mathematical community will do once more in what they are best: ignore all things Reinko Venema related, look the other way, ask for more funding and so on and so on. In my life and life experiences not one university person has ever made a positive difference, all those people are only occupied with how important they are and that’s it. Being mathematical creative is not very high on the list of priorities over there, only conform to a relatively low standard of ‘common talk’ is acceptable behavior…

After having said that, this post is partitioned into five parts and is 10 pictures long. It is relatively basic and in case that for example you have never looked at matrix representations of complex numbers of any dimension, please give it a good thought.

Because in my file I also encountered a few of those professional math professors that were rather surprised by just how a 3 by 3 matrix looks for 3D complex numbers. How can you find that they asked, but it is fucking elementary linear algebra and sometimes I think these people do not understand what is in their own curriculum…

Ok, here are the 10 pictures covering the basic details of 4D complex numbers:

Ok, that was the math for this post.

And may be I am coming a bit too hard on the professional math professors. After all they must give lectures, they must attend meetings where all kinds of important stuff has to be discussed until everybody is exhausted, they must be available for students with the questions and problems they have, they must do this and must do that.

At the end of the day, or at the end of the working week, how much hours could they do in free thinking? Not that much I just guess…

Let’s leave it with that, see you in the next post.

Calculation of the 4D complex number tau.

April 18, 20184D complex numbers, Exponential curves, Matrix representation, Quantum mechanicsReinkoVenema

It is about high time for a new post, now some time ago I proposed looking at those old classical equations like the heat and wave equation and compare that to the Schrödinger equation. But I spilled some food on my notes and threw it away, anyway everybody can look it up for themselves; what often is referred to as the Schrödinger equation looks much more like the heat equation and not like the classical wave equation…

Why this is I don’t know.

This post is a continuation from the 26 Feb post that I wrote after viewing a video from Gerard ‘t Hooft. At the end of the 26 Feb post I showed you the numerical values for the logarithm of the 4D number tau. This tau in any higher dimensional number system (or a differential algebra in case you precious snowflake can only handle the complex plane and the quaternions) is always important to find.

Informally said, the number tau is the logarithm of the very first imaginary component that has a determinant of 1. For example on the complex plane we have only 1 imaginary component usually denoted as i. Complex numbers can also be written as 2 by 2 matrices and as such the matrix representation of i has a determinant of 1.
And it is a well known result that log i = i pi/2, implicit the physics professors use that every day of every year. Anytime they talk about a phase shift they always use this in the context of multiplication in the complex plane by some number from the unit circle in the complex plane.

In this post, for the very first time after being extremely hesitant in using dimensions that are not a prime number, we go to 4D real space. Remark that 4 is not a prime number because it has a prime factorization of 2 times 2.

Why is that making me hesitant?
That is simple to explain: If you can find the number i from the complex plane into my freshly crafted 4D complex number system, it could very well be this breaks down to only the complex plane. In that case you have made a fake generalization of the 2D complex numbers.

So I have always been very hesitant but I have overcome this hesitation a little bit in the last weeks because it is almost impossible using the complex plane only to calculate the number tau in the four dimensional complex space…

May be in a future post we can look a bit deeper in this danger; if also Cauchy-Riemann equations are satisfied in four real variables, that would bring a bit more courage to further study of the 4D complex number system.

__________

After the introduction blah blah words I can say the 4D tau looks very beautiful. That alone brings some piece of mind. I avoided all mathematical rigor, no ant fucking but just use numerical results and turn them into analytical stuff.

That is justified by the fact that Gerard is a physics professor and as we know from experience math rigor is not very high on the list or priorities over there…

That is forgiven of course because the human brain and putting mathematical rigor on the first place is the perfect way of making no progress at all. In other sciences math should be used as a tool coming from a toolbox of reliable math tools.

__________

This post is seven pictures long, all are 550 by 775 pixels in size except for the last one that I had to make a little bit longer because otherwise you could not see that cute baby tau in the 4D complex space.

Here we go: