Category Archives: Matrix representation

The scalar replacement theorem.

CR equations, Matrix representation

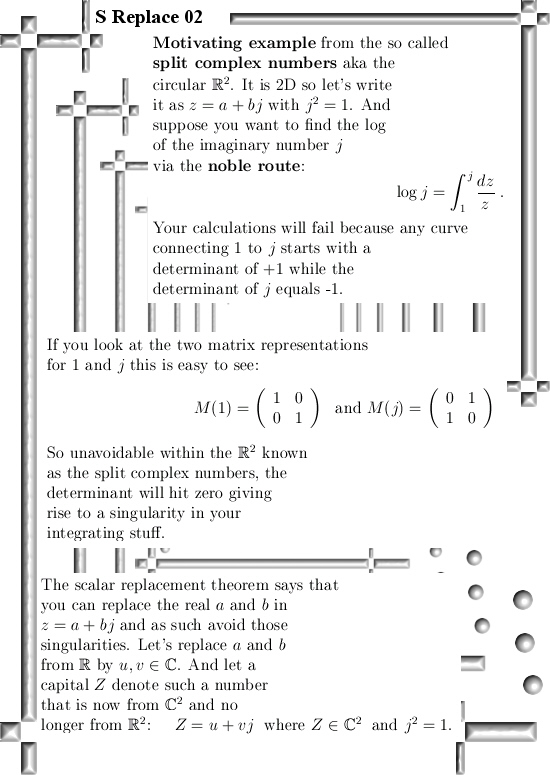
Ok ok I was a bit lazy but it is finished now so let’s finally post this scalar replacement theorem. Never in this post I formulate or proof this scalar replacement theorem, but basically this theorem says that if you replace the real numbers (scalars) in the way you describe say 2D split complex numbers by numbers from the complex plane, the result is a space who’s numbers also commute and it even has viable Cauchy Riemann equations. In this post I will write z = x + yj for the 2D circular numbers (also known as the split complex numbers) and write z = x + yi for numbers from the complex plane. If you combine such spaces it must have imaginary units that are different in notation, so j is the imaginary unit that does j^2 = 1 while the good ol i from the complex plane is known for it’s important property that i^2 = -1.

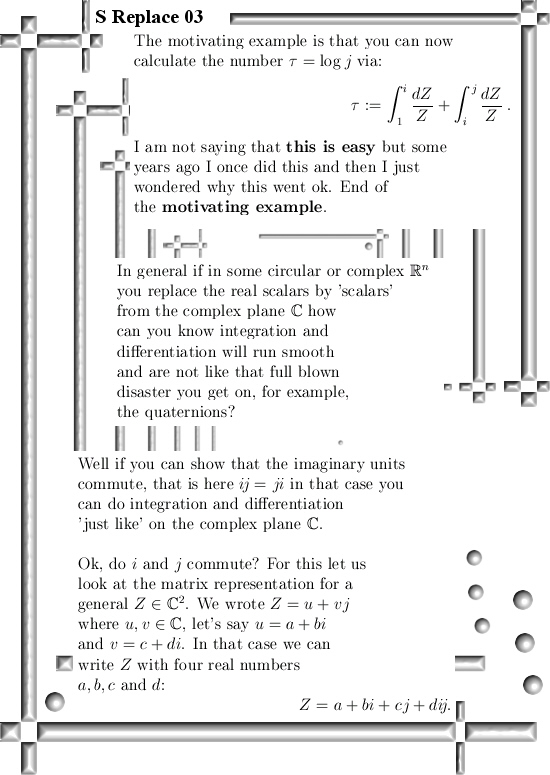
If we replace the x and y in z = x + yj by complex numbers we get a new 4D space where both j and i place there role. All in all those 4D numbers will be written as Z = a + bi + cj + dij. Of course the a, b, c and d are real numbers and as such this new space is 4D.

A long time ago I once used this to calculate the logatithm of j, it worked perfectly and that is why I more or less gave idea’s like that the name of ‘scalar replacement’. Later I found that way of using diagonalization of the matrix representations in order to calculate the logarithm, that is a far more general useable way of calculating logarithms but anyway the original calculation for log j was so cute, I could not abondon it and say to that calculation: From now on you are a poor orphan and no one will help you survive from day to day… How could I abandon such a calculation, better loose the UK a 100 times on a row than abandoning such nice calculations… 😉

But let’s go back to being a serious and responsible adult; the post is relatively long with 10 pictures. As usual I had to leave a lot out and I hope it is more or less easily readable. After all a lot of math out there looks like it is written by people who eat a plate of coal for breakfast. And if you eat coal for breakfast, likely this has an influence on the math you will produce on a particular day… Ok, here we go:

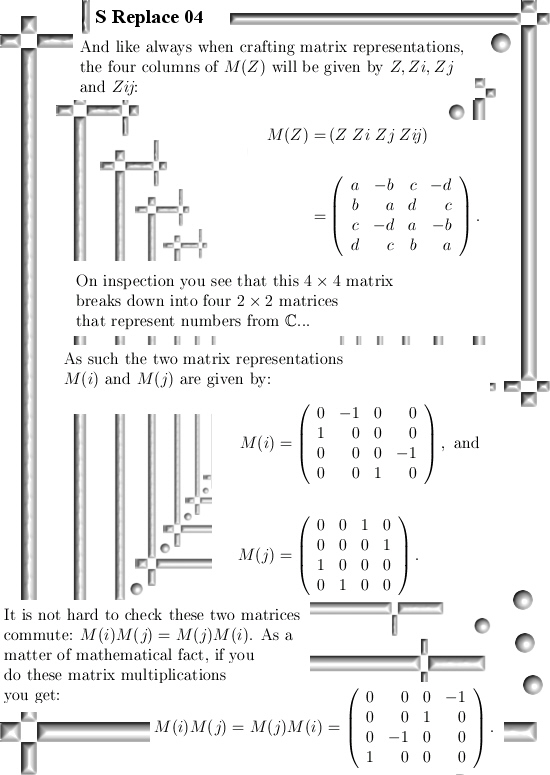
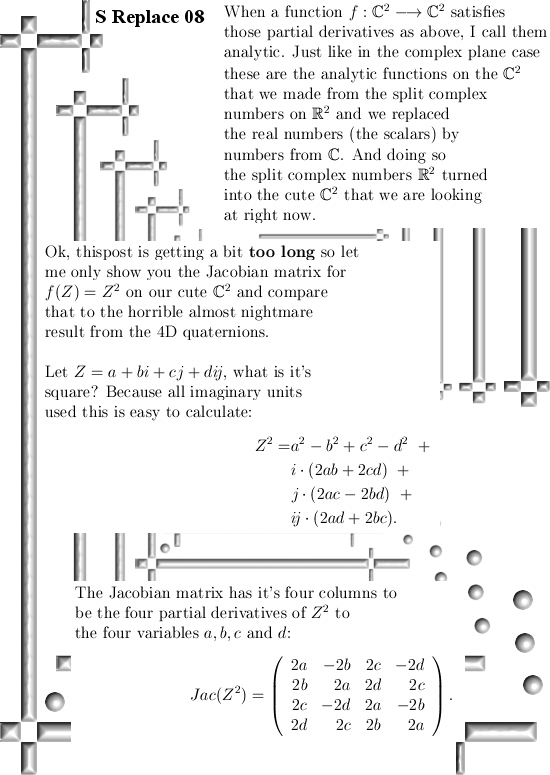
Ok, the goal of this post is of course to make you think a little bit about this 4D space and compare it to the quaternions and stuff. But last year on 2 March I posted the diagonalization method for finding the logarithm of an arbitrary split complex number. Below is a link.

The logarithm of all 2D circular numbers (the split complex numbers).

Let me end this post with a funny mathematical joke about how to NOT WRITE MATH. Using a fucking lot of indices is not a way to make your work readable, here is a picture of what I view as some kind of mathematical joke.

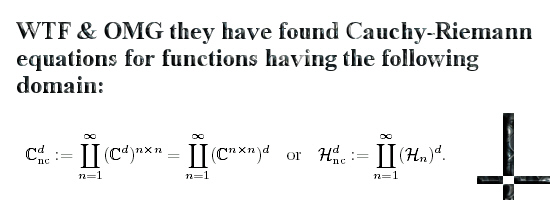
In case you desire a serious headache, go read that file.

https://arxiv.org/pdf/1906.09014.pdf

Ok, end of this post.

The sphere-cone equation in a matrix notation.

3D complex numbers, Exponential circle, Matrix representation

It is about time for a new post on 3D numbers, circular and complex. In this post I write the sphere-cone equation in a matrix notation so see the previous post on conjugates if you feel confused. The sphere-cone equation gives us two equations, as the name suggests these are a sphere and a cone and on the intersection we find the famous exponential circle.

Beside the sphere-cone equation I also demand that the determinant equals 1, now we have three equations and every intersection of those 3 equations has as it’s solution the exponential circle. Can it become more crazy? Yes because it is possible to factorize the third degree determinant into a linear and a quadratic factor. Those factors must also be 1 and now we have five equations! And since you can pick 10 pairs out of five, we now have 10 ways of solving for the intersection where the exponential circle lives…

It is strange that after all these years it is still easy to find 10 video’s where so called ‘professional math professors’ sing their praise upon the exponential circle in the complex plane. They really go beserk over the fact that e to the power it gives the cosine and sine thing. And after all those years still silent, yeah yeah those hero’s really deserve the title of honorable shithole… It is honorable because they often have relatively large salaries and they are shitholes because of their brave behavior when it comes to 3D complex numbers. Bah, I am getting a bad taste in my mouth when I think about the behavior of professional math professors. Let me stop writing about that low form of life.

This post is 8 pictures long. May be, I have not decided yet, is the next post about parametrizations of the exponential circle. In these 8 pictures I work out the case for the circular multiplication, that is the case where the imaginary unit j behaves like j^3 = 1. At the end I only give the 3D complex version of the matrix form of the sphere-cone equation and the rest you are supposed to do yourself.

Ok, again do not confuse this with quadratic forms. A matrix equation as written above has a real and two imaginary components while quadratic forms are often just real valued.

Let´s try to upload this stuff. See you in the next post.

The two self-conjugate planes for 3D circular and complex numbers.

3D complex numbers, Matrix representation

This is another lightweight easy going summer update. It is about matrix representations and how to find the conjugate of a 3D complex or circular number. I use the case of the complex plane of 2D conplex numbers to show that conjugation is not some silly reflection just always but rather simple will always be the upper row of a proper matrix representation. As a matter of fact it is so easy to understand that even the biggest idiots on this planet could understand it if they wanted. Of course math professors don’t want to understand 3D numbers so also this new school year nothing will happen on that front…

Did you know that math professors study the periodic system? Yes they do, anyway in my home country the Netherlands they do because every year they get a pay rise and that pay rise is called a periodic. And as such they study the periodic system deep and hard…

I classified this post only under the categories ‘3D complex numbers’ and ‘matrix representations’ and left all stuff related to exponential circles out. Yet the exponential circle stuff is interesting; after reading this post try to find out if the numbers alpha (the midpoint of the exponential circles) are symmetrix (yes). And the two numbers tau (the log of the first imaginary unit on the circular and complex 3D space) are anti-symmetrix (yes).

This post is just over 7 pictures long. As the background picture I used the one I crafted for the general theorem of Pythagoras. (Never read that one? Use the search funtion for this website please!) All pictures are of the usual size namely 550×775 pixels.

It is a cute background picture, I remember it was relatively much work but the result was fine.

Ok, that was it for this update. Although it is so very simple (for years I did not want to write of just two simple planes that contain all the self-conjugate numbers) but why make it always so difficult? Come on it is summer time and in the summer almost all things are more important than math. For example goalkeeper cat is far more important compared to those stupid 3D numbers. So finally I repost a video about a cat and that makes me very similar to about 3 billion other people.

Till updates & thanks for your attention.

But are these quadratic forms?

3D complex numbers, Exponential circle, Matrix representation

This is a lazy easy going summer post, it does not have much mathematical depth. Let’s say the depth of a bird bath. But with most posts I write you also need a lot of knowledge about what was in previous posts and for the average person coming along that is often too time consuming… So we keep it simple today; quadratic forms on 3D space.

If you have had one or two courses of linear algebra you likely have encountered quadratic forms. They are often denoted as Q(X) where the X is a column matrix and the quadratic form is defined as Q(X) = XT A X. Here XT is the transponent of X so that would be a matrix row. As you might guess, the X column matrix contains the variables while the constant square matrix A is the source of coefficients in the quadratic form Q(X).  In most literature it is told the matrix A is symmetric, of course there is no reason at all for that; any square matrix will do. On the other hand it is easy to see or to show that if a square matrix is anti-symmetric the corresponding quadratic form will always be zero everywhere.

In this post we will take matrices that are always the matrix representation of 3D complex & circular numbers. Matrix representations are a complete category on this website so if you don’t know them you must look that up first. (Oh oh, here I go again: this was supposed to be easy but now the average reader must first try to understand matrix representations of higher dimensional multiplications…)

Compared to the previous update on the likely failure of all fusion reactors this post is far less dramatic. If in the future I am right and we will never have fusion power, that will be the difference between life and death of hundreds of millions of people in the long run… So in order to be a bit less depressing let’s lift the spirits by a lightweight new post on quadratic forms! Why not enjoy life as long as it lasts?

Ok, the actual post is seven pictures long, all in the usual size of 550×775 pixels.













As you see the math is only bird bath deep.

I have to admit that for me the use of the number alpha was important because that is at the center of the exponential circles in the 3D complex and circular spaces. So I have a legitimate reason to post this also under the category ´exponential circle´. And from the non-bird bath deep math, that is the big math ocean that is very deep, I like to classify as much posts under that category ´exponential circles´.

Ok, let´s leave it with that and try to upload this post. Till updates my dear reader.

Using the Cayley-Hamilton theorem to find ‘all’ multiplications in 3D space.

3D complex numbers, CR equations, Matrix representation, Uncategorized

It is a bit vague what exactly a multiplication is, but I always use things that ‘rotate over the dimensions’. For example on the 3D complex space the imiginary unit is written as j and the powers of j simply rotate over the dimensions because:

j = (0, 1, 0)
j^2 = (0, 0, 1) and
j^3 = (-1, 0, 0). Etc, the period becomes 6 in this way because after the sixth power everything repeats.

In this post we will look at a more general formulation of what the third power of j is. The Cayley-Hamilton theorem says that you can write the third power of 3 by 3 matrices always as some linear combination of the lower powers.

That is what we do in this post; we take a look at j^3 = a + bj + cj^2. Here the a, b and c are real numbers. The allowed values that j^3 can take is what I call the ‘parameter space’. This parameter space is rather big, it is almost 3D real space but if you want the 3D Cauchy-Riemann equations to fly it has to be that a is always non zero. There is nothing mysterious about that demand of being non zero: if the constant a = 0, the imaginary unit is no longer invertible and that is the root cause of a whole lot of trouble and we want to avoid that.

It is well known that sir Hamilton tried to find the 3D complex numbers for about a full decade. Because he wanted this 3D complex number space as some extension of the complex plane, he failed in this detail and instead found the quaternions… But if the 3D numbers were some extension of the 2D complex plane, there should be at least one number X in 3D such that it squares to minus one. At the end I give a simple proof why the equation X^2 = -1 cannot be solved in 3D space for all allowed parameters. So although we have a 3D ocean of parameters and as such an infinite amount of different multiplications, none of them contains a number that squares to minus one…

I gave a small theorem covering the impossibility of solving X^2 = -1 a relative harsh name: Trashing the Hamilton approach for 3D complex numbers. This should not be viewed as some emotional statement about the Hamilton guy. It is just what it says: trashing that kind of approach…

This post is 7 pictures long, each of the usual size of 550×775 pixels.

Test picture, does jpg upload again?












Sorry for the test picture, but the seven jpg pictures refused to upload. And that is strange because they are just seven clean jpg’s. Now it is repaired although I do not understand this strange error.

Anyway have a cool summer. Till updates.

The Cayley-Hamilton theorem neglected for 25 years?

3D complex numbers, Matrix representation, Uncategorized

That is strange, if you don’t know the Cayley-Hamilton theorem; it is the finding that every square matrix A, if you calculate the characteristic polynomial for the matrix A it is always zero. At first this is a very surprising result, but it is easy to prove. It’s importance lies in the fact that in this way you can always break down higher powers of the matrix A in lower powers. In the study of higher dimensional complex and circular numbers we do this all the time. If in 3D space I say that the third power of the imaginary component is minus one, j^3 = -1, we only write the third power as a multiple of the zero’th power…

In this post I will give two simple proofs of the Cayley-Hamilton theorem and although in my brain this is just a one line proof, if you write it down it always gets longer than anticipated.

At the end I show you an old video from the year 1986 from the London Mathematical Society where it is claimed that the CH theorem was neglected for 25 years. Now Hamilton is also famous for having sought the 3D complex numbers for about a full decade before he gave up. And I still do not understand why Hamilton tried this for so long but likely he wanted to include the imaginary unit i from the complex plane in it and that is impossible. Or may be he wanted a 3D complex number system that is also a field (in a field all elements or numbers that are non-zero have an inverse, in algebra wordings; there are no divisors of zero). A 3D field is also impossible and in this post I included a small proof for that.

Furthermore in this post at some point may be you read the words ‘total incompetents’ and ‘local university’. You must not view that as some emotional wording, on the contrary it is a cold clinical description of how math goes over there. So you must not think I am some kind of frustrated person, for me it is enough that I know how for example to craft a 3D complex number system. If they don’t want to do that, be my guest. After all this is a free country and we also have this concept of ‘academic freedom’ where the high shot math professors can do what they want.

And what is this ‘academic freedom’ anyway? If for example unpaired electrons are never magnetically neutral but electron pairs always are magnetically neutral, can the physical reality be that electrons are magnetic dipoles? Of course not, that is a crazy idea to begin with. But 97 years of academic freedom since the Stern-Gerlach experiment have never ever brought any meaningful understanding of the magnetic properties of the electron. If it acts as a magnetic charge and you say it is not a charge it is easy to understand how you can fool yourself for about one century of time.

This post is seven pictures long although the last picture is empty.
The two proofs of the Cayley/Hamilton theorem is how I would prove such a thing but good theorems always have many proofs. All pictures are of the size 550×775 pixels.













Why is the seventh picture without math?

Here is the old video from 1986 where it is claimed the Cayley-Hamilton theorem was neglected for about 25 years. Oh oh oh what a deep crime. But the human mind is not made to produce or understand math, so in my view 25 years is a short period of time if in the good old days math professors were equally smart as the present day math professors. The title of the video is The Rise and Fall of Matrices.

Matrices saved my life from crazy math professors.

Ok let me leave it with that an not post a link to the top wiki on the Cayley-Hamilton theorem where all kinds of interesting proofs are given. Till updates my dear reader.

Part 18: Calculating the 4D number tau it’s inverse in a very simple way.

4D complex numbers, Matrix representation

It is the shortest day of the year today and weirdly enough I like this kind of wether better compared to the extreme heat of last summer. Normally I dislike those long dark days but after so much heat for so long I just don’t mind the darkness and the tiny amounts of cold.

In the previous post we found a general way of finding all inverses possible in the space of the 4D complex numbers. Furthermore in the post with the new Cauchy integral representation we had to make heavy use of 1/8tau and as such it is finally time to look at what the inverse of tau actually is.

I found a very simple way of calculating the inverse of the number tau. It boils down to solving a system of two linear equations in two variables. As far as I know reality, most math professionals can actually do this. Ok ok, for the calculation to be that simple you first must assume that the inverse ‘looks like’ the number tau in the sense it has no real component and it is just like tau a linear combination of those so called ‘imitators of i‘.

This is a short post, only five pictures long. I started the 4D complex number stuff somewhere in April of this year so it is only 8 month down the timeline that we look at the 4D complex numbers. It is interesting to compare the behavior of the average math professor to back in the time to Hamilton who found the 4D quaternions.

Hamilton became sir Hamilton rather soon (although I do not know why he became a noble man) and what do I get? Only silence year in year out. You see the difference between present day and past centuries is the highly inflated ego of the present day university professors. Being humble is not something they are good at…

After having said that, here are the five pictures:

All in all I have begun linking the 4D complex numbers more and more in the last 8 months. On details the 4D complex numbers are very different compared to 3D and say 5D complex numbers but there are always reasons for that. For example the number tau has an inverse in the space of 4D complex numbers but this is not the case in 3 or 5D complex numbers space.

Well, have a nice Christmas & likely see you in the next year 2019.

Part 17: The inverse of a 4D complex number old school style (via minor matrices).

4D complex numbers, Matrix representation

Ha, a couple of weeks back I met an old colleague and it was nice to see him. We made a bit of small talk and more or less all of a sudden he said: ‘But you still can always do this’. And he meant getting a PhD in math. 

I was a bit surprised he did bring this up, for me that was a station passed long ago. But he made me thinking a bit, why am I not interested in getting a math degree? 

And when I thought it out I also had to laugh: Those people cannot go beyond the complex plane for let’s say 250 years. And the only people I know of that have studied complex numbers beyond the complex plane are all non-math people. Furthermore inside math there is that cultural thing that more or less says that if you try to find complex numbers beyond the complex plane, you must have a ‘mental thing’ because have you never heard of the 2-4-8 theorem? 

Beside this, if I tried it in the years 1990 and 1991 with very simple: Here this is how the 3D Cauchy Riemann equations look… And you look them in the eyes, but there is nothing happening behind those eyes or in the brain of that particular math professor. Why the hell should I return and under the perfect guidance of such a person get a PhD? 

I am not a masochist. If complex numbers beyond the complex plane are ignored, why try to change this? After all this is a free world and most societies run best when people can do what they are good at. Apparently math like I make simply falls off the radar screen, I do not have much problems with that. 

___________

After having said that, this update Part 17 in the basics to the 4D complex numbers is as boring as possible. Just finding the inverse of a matrix just like in linear algebra with the method of minor matrices.

Believe me it is boring as hell. And after all that boring stuff only one small glimmer of light via crafting a very simple factorization of the determinant inside the 4D complex numbers. So that is very different from the previous factorization where we multiplied the four eigenvalue functions. From the math point it is a shallow result because it is so easy to find but when before your very own eyes you see the determinant arising from those calculations, it is just beautiful. And may be we should be striving a tiny bit more upon mathematical beauty…

This post is nine pictures long in the usual size of 550×775 pixels.

 

As an antidote against so much polynomials like det(Z), with 2 dimensions like a flatscreen television, you can do a lot of fun too. The antidote is a video from the standupmaths guy, it is very funny and has the title ‘Infinite DVD unboxing video: Festival of the Spoken Nerd’. Here is the vid:

End of this update, see you around.

Ok ok, a few days later I decided to write a small appendix to this post and in order too keep it simple let’s calculate the determinant of the 3D circular numbers. I have to admit this is shallow math but despite being shallow it gives a crazy way to calculate the determinant of a 3D circular number…

So a small appendix, here it is:

And now you are really at the end of this post.

In the next post let’s calculate the inverse of the 4D complex tau number. After all a few months back I gave you the new Cauchy integral representation and I only showed that the determinant of tau was nonzero.

But the fact that the Cauchy integral representation is so easy to craft on the 4D complex numbers arises from the fact the inverse of tau exists in the first place. In 3D the number tau is not invertible, and Cauchy integral representations are much more harder to find.

Ok, drink a green tea or pop up a fresh pint, till updates.

Calculation of the 4D number tau diagonal matrix style.

4D complex numbers, Exponential curves, Matrix representation

In the begin of this series on basic and elementary calculations you can do with 4D complex numbers we already found what the number tau is. We used stuff like the pull back map… But you can do it also with the method from the previous post about how to find the matrix representation for any 4D complex number Z given the eigenvalues.

Finding the correct eigenvalues for tau is rather subtle, you must respect the behavior of the logarithm function in higher dimensions. It is not as easy as on the real line where you simply have log ab = log a + log b for positive reals a and b.

But let me keep this post short and stop all the blah blah.

Just two nice pictures is all to do the calculation of the 4D complex number tau:

 

(Oops, two days later I repaired a silly typo where I did forget one minus sign. It was just a dumb typo that likely did not lead to much confusion. So I will not take it in the ‘Corrections’ categorie on this website that I use for more or less more significant repairs…)

Ok, that was it.

Diagonal matrices for all 4D complex numbers.

4D complex numbers, Exponential curves, Matrix representation

This website is now about 3 years old, the first post was on 14 Nov 2015 and today I hang in with post number 100. That is a nice round number and this post is part 15 in the series known as the Basics for 4D complex numbers.

We are going to diagonalize all those matrix representations M(Z) we have for all 4D complex numbers Z. As a reader you are supposed to know what diagonalization of a matrix actually is, that is in most linear algebra courses so it is widely spread knowledge in the population.

Now at the end of this nine pictures long post you can find how you can calculate the matrix representation for M(l) where l is the first imaginary unit in the 4D complex number system. And I understand that people will ask full of bewilderment, why do this in such a difficult way? That is a good question, but look a bit of the first parts where I gave some examples about how to calculate the number tau that was defined as log l. And one way of doing that was using the pull back map but with matrix diagonalization you have a general method that works in all dimensions.

Beside that this is an all inclusive approach when it comes to the dimension, in practice you can rely on internet applets that use commonly known linear algebra. Now if you are a computer programmer you can automate the process of diagonalization of a matrix. I am very bad in writing computer programs, but if you can write code in an environment where you can do symbolic calculus in your code, it would be handy if that is on such a level you can use the so called roots of unity from the complex plane. After all the eigenvalues you encounter in the 4D complex number system are always based on these roots of unity and the eigenvectors are too…

This post number 100 is 9 pictures long, as usual picture size is 550 x 775 pixels.
In the next post number 101 we will use this method to calculate the matrix representation of the number tau (that is the log of the first imaginary unit l).

Ok, here are the pictures:

That´s it, in the next post we go further with the number tau and from the eigenvalues of tau calculate the matrix representation. So see you around.