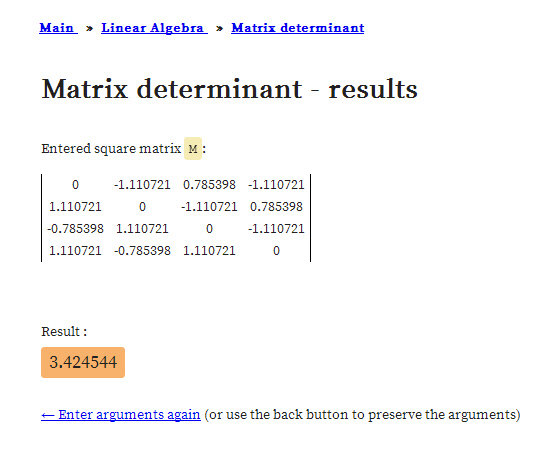
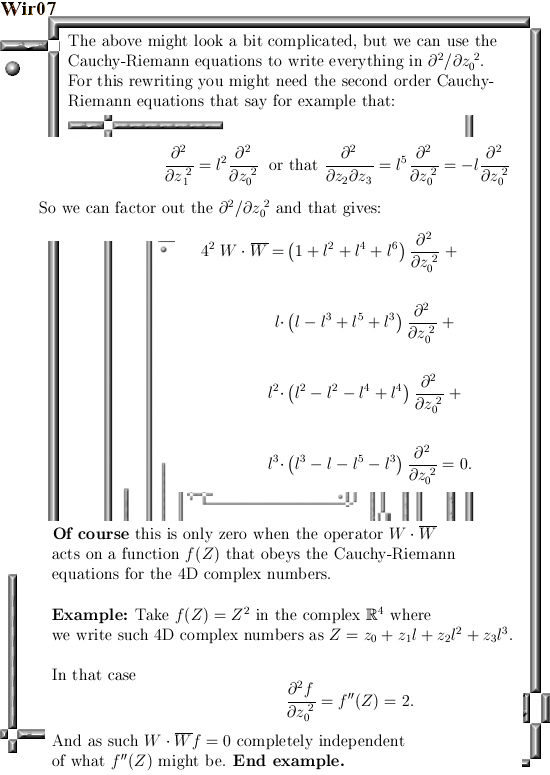
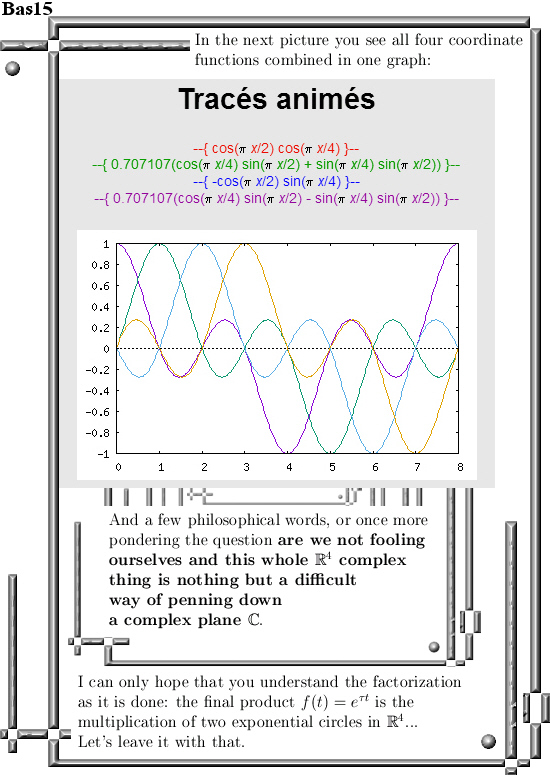
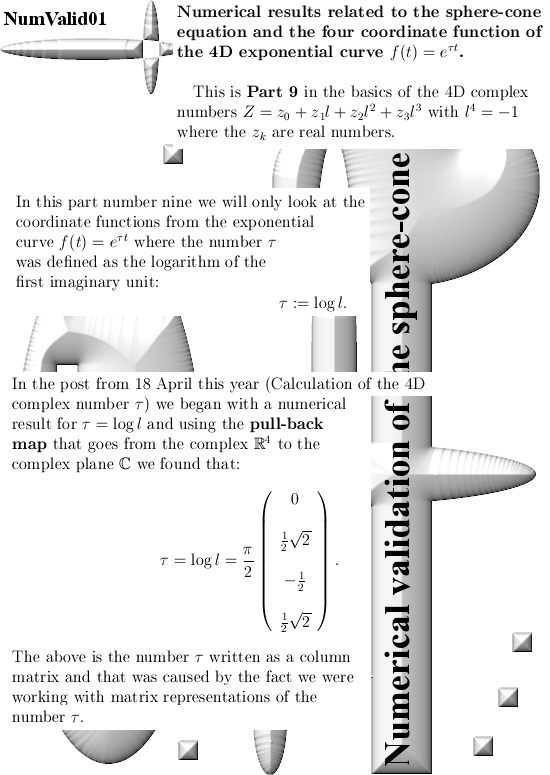
This is Part 9 in the basics to the complex 4D numbers. In this post we will check numerically that the 4D exponential curve has it’s values on the 4D unit sphere intersected with a 4D cone that includes all coordinate axes. In 3D space the sphere-cone equations ensure the solution is 1 dimensional like a curve should be. In 4D space the sphere-cone equations are not enough, there is at least one missing equation and those missing equations can be found in the determinant of a matrix representation M(Z) for a 4D complex number Z.
But we haven’t done any determinant stuff yet (because you also need a factorization of the 4D determinant in four variables and that is not a trivial task). So this post does not contain numerical evidence that the determinant is always one on the entire exponential curve.
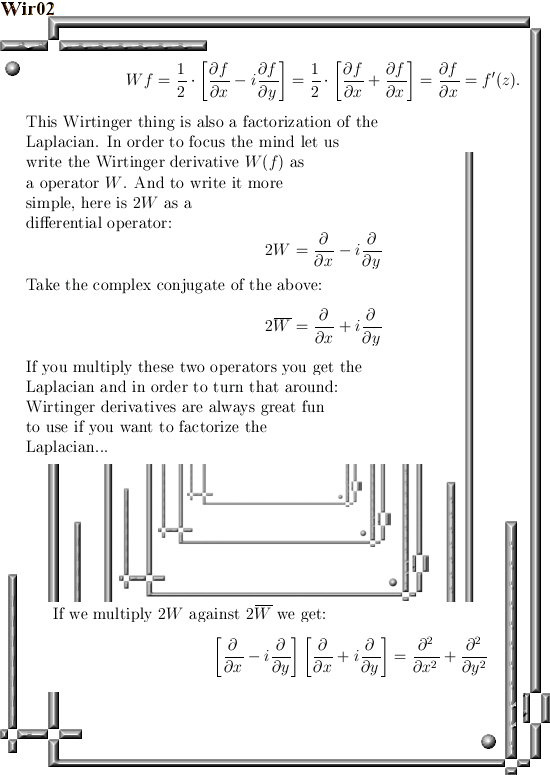
If you want to compare this post to the same stuff in the complex plane:
In the complex plane the sphere-cone equation is given by x^2 + y^1 = 1 (that is the unit circle) and if you read this you probably know that f(t) = e^{it} = cos t + i sin t.
You can numerically check this by adding the squares of the sine and cosine for all t in one period and that is all we do in this post. Only it is in 4D space and not in the two dimensional complex plane…
This post is seven pictures long (all of the usual size 550 x 775).



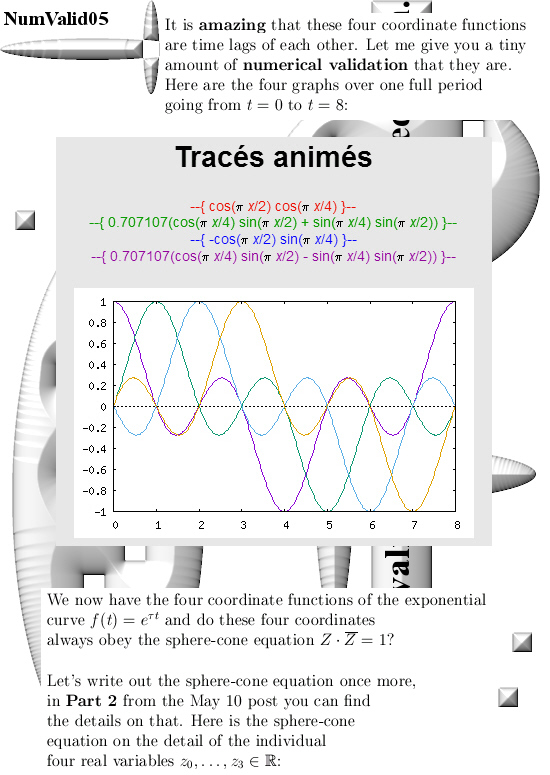

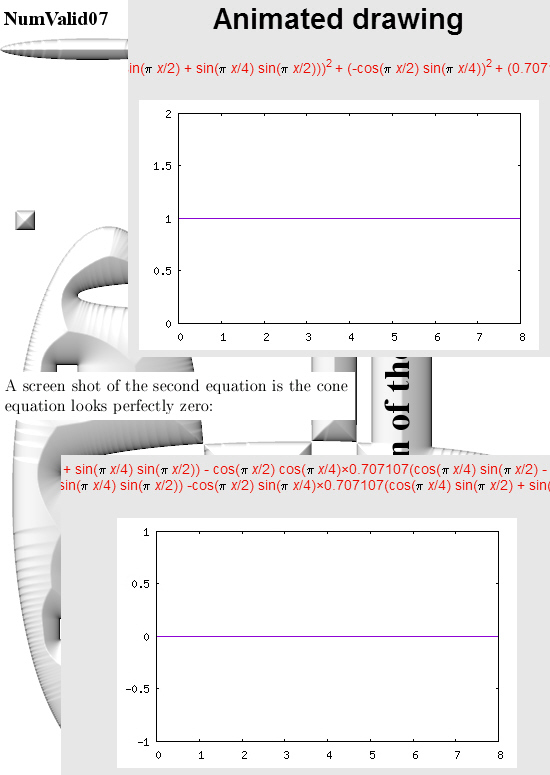
All graphs in this post are made with the applets as found on:
WIMS https://wims.sesamath.net/wims.cgi?lang=en
For the two graphs from above look for ‘animated drawing’ choose the 2D explicit curves option. There you must use the variable x instead of time t.
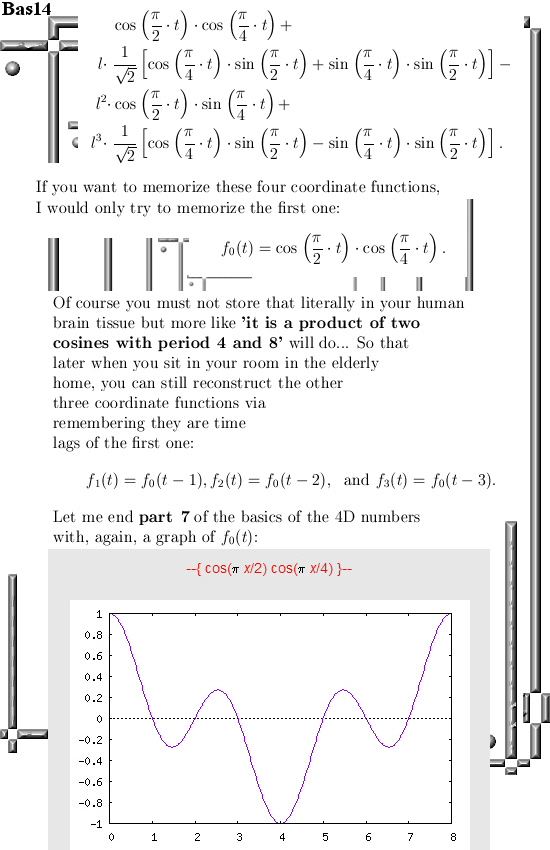
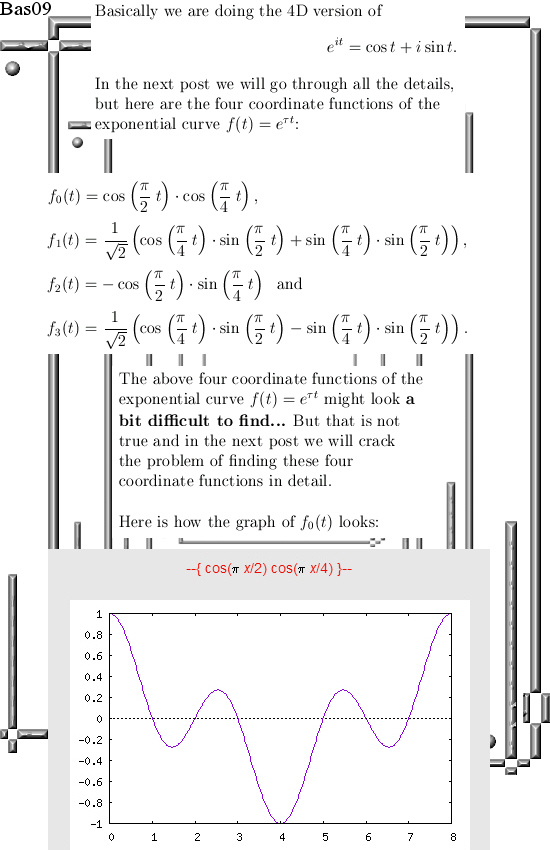
Here is the stuff you can place in for the sphere equation:
(cos(pi*x/2)*cos(pi*x/4))^2 +
(0.707107*(cos(pi*x/4)*sin(pi*x/2) + sin(pi*x/4)*sin(pi*x/2)))^2 +
(-cos(pi*x/2)*sin(pi*x/4))^2 +
(0.707107*(cos(pi*x/4)*sin(pi*x/2) – sin(pi*x/4)*sin(pi*x/2)))^2
If you just ‘cut & paste’ it should work fine…
That should save you some typo’s along the way
Ok, that is what I had to say on this numerical detail.