The zero’s of the Riemann zeta function is one the things I will never be able to find because I hate it to write computer code. Always my original enthousiasm fades away quickly and after some time I simply stop working in that direction and foces on things that I like more.

Just like a few posts back when I finally decided to skip the stupid Mandelbrot fractal in three dimenstions. Computers are nice things to build but programming has never been my cup of tea let alone my pint of beer. (I am also a hobby brewer, it is a great hobby and it saves you a lot of money. The more you brew the more money you save…).

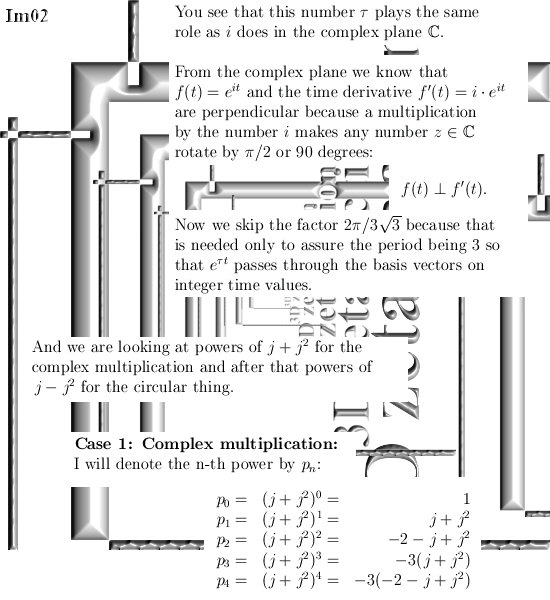
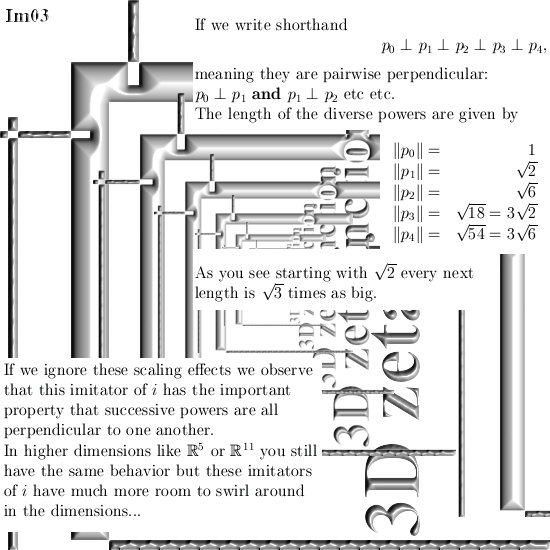
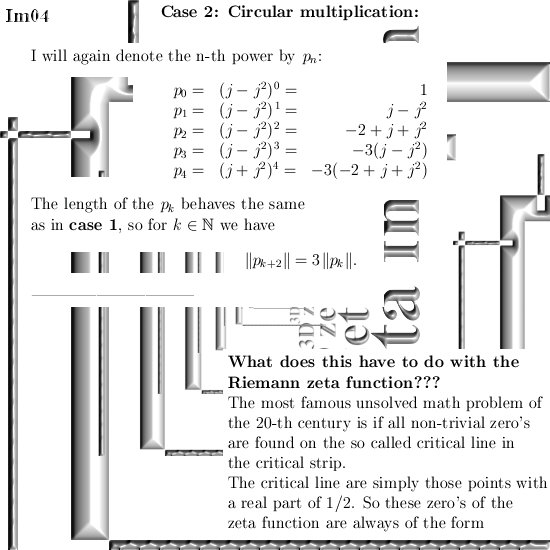
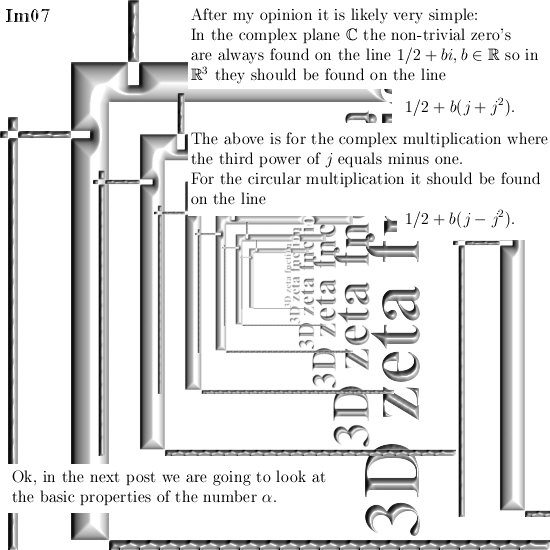
Ok in this update we are going to take a look at imitators of the number i from the complex plane. I think that most readers here already know that multiplication by i rotates everything 90 degrees. In 3D space we have similar things but not all higher dimensional number spaces contain the number i from the complex plane. In that case we must use substitutes like what I name the ‘imitators of i‘.

This update is seven pictures long, each picture is 550 by 550 pixels:

In the next post we will flea through the elementary properties of the number alpha, look at the dynamics on the line through zero and alpha (just like on the real line) and so on and so on.
Till updates.