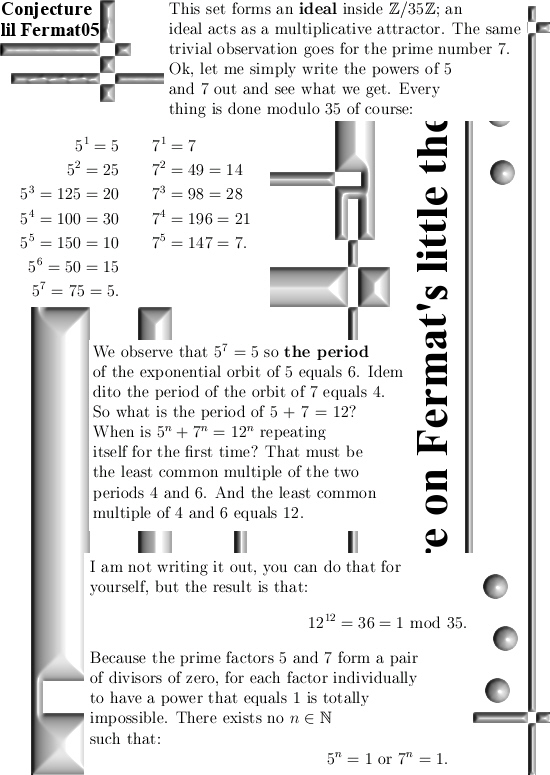
This is not a totally new proof, basically it is already part of the proof in the previous post. But I was able to write it down a bit more compact. It seems that you can skip large parts of the previous proof and still the result is standing. The stuff you can skip is not unimportant or so; it is where I compared those additive and multiplicative orbits and you really need that in order to understand a bit more of what is happening in rings like the integers modulo 35 (or any other composite number of course).
Often I name the ordinary intergers ‘real integers’. I hope that is not confusing, with a real integer I mean whole numbers as they are found on the real line. I do that do make clear the difference with the Gaussian integers as they are found in the diverse complex spaces.

Right now I am already about four months busy with this stuff that all started in January with counter examples to the last theorem of Fermat. All in all I never expected to be able to make an improvement on the little theorem of Fermat. But sometimes the old little theorem gives answers that are indeed correct but still is not that satisfactory. In the old little theorem you take some real integer a, you pick a prime number p that has no common factors with a and you know that in that case:
a^p mod p = a. But if the prime number p is relatively small, I mean a is larger, you don’t get back a but a mod p.

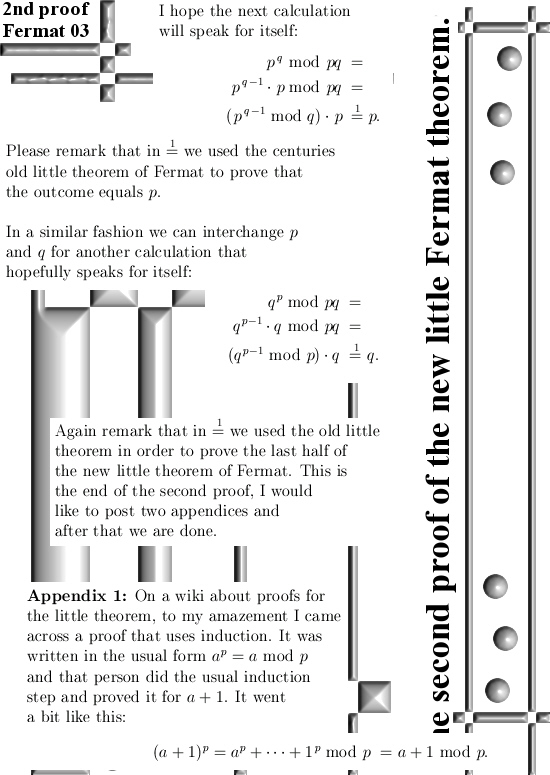
This post is short, only three pictures in the usual format of 550×775 pixels but I added two appendices so all in all there are five pictures in this post. In the second appendix I show you that if we square 125, the old little theorem gives back a 1 while my new version of the little theorem nicely gives back 125. Of course there is always much discussion possible of something is ‘better’ or not. It is only in the sense that also with small prime numbers you get back your a I mean it is ‘better’. One thing is clear: it is definitely more beautiful. My favorite formulation stays the formulation with two prime numbers like in:

p^q = p mod pq &
q^p = q mod pq.

The symmetry in the pair of equations above is, in my opinion, more beautiful compared to the old version of the little theorem of Fermat. At last I want to remark that I have a thing in common with Monsieur Fermat: math is a hobby for me. Now the old little theorem was improved upon by the professional professor Euler and with a little smile on my face I can say: Hey Euler did you miss the above pair of cute equations?

Yes he did, just like a guy named Einstein never had a fucking clue about electron spin. But likely that is a story for another day, in the meantime we have five pictures with the second proof of the new little theorem. Have fun reading it and never forget: If it is math, sometimes you need a few more days to figure it all out!

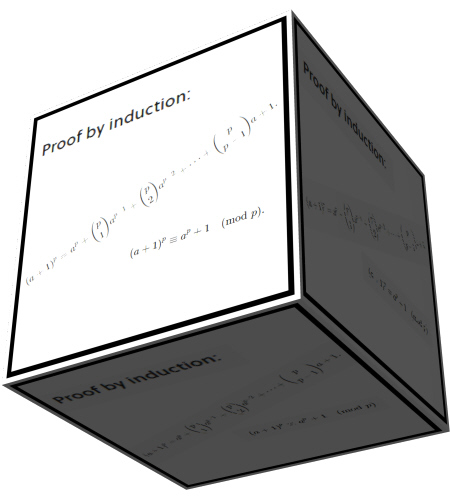
In a wiki upon proofs of the little Fermat theorem you can find that one of the authors did indeed find a counter example to the last theorem of Fermat. You can find it under ´Multinomial proofs´in the next link:
Proofs of Fermat´s little theorem. Link used:
https://en.wikipedia.org/wiki/Proofs_of_Fermat%27s_little_theorem

Ok, that was it for this post. Thanks for your attention.

The proof is finished and in the end it went rather different from what I expected before the writing down of this new proof. I hope the main ideas are easy to understand. I formulated the proof with a concrete example; so not two general prime number p and q. But I took p = 5 and q = 7 and as such we are calculating in the ring of integers modulo 35.
One of the key ideas is that we have so called additive orbits, for example the additive orbit of 5 is the set {0, 5, 10, 15, 20, 25, 30}. The additive orbit are just the multiples of 5, it is handy to view the above set as multiples of five and as such: {0, 5, 2*5, 3*5, 4*5, 6*5}.
On the other hand we have exponential orbits, the exponential orbit of 5 are the powers of 5 like in the next sequence: 5, 5^2, 5^3, 5^4…
An important observation is that any power of five is also a multiple of five; that means the exponential orbit is inside the additive orbit. For example 5^3 is on the exponential orbit, 5^3 = 125 = 20 modulo 35 = 4* 5.
So the number 5^3 from the exponential oribt corresponds to 4*5 on the additive orbit. The goal of the proof is to show that the period of 5 in her exponential oribt is 6 and the period of the exponential orbit of 7 is 4.
That will ensure our new little theorems of Fermat:
p^q = 5^7 = 5 modulo 35 &
q^p = 7^5 = 7 modulo 35.
Remark that powers of 5 can never be a multiple of 35 simply because any power of 5 does not contain a prime factor 7, so not all of the numbers on the additive orbit are allowed.
Another key idea is that if we reduce stuff modulo 35, this is the same as reducing stuff modulo 7 on the multiples of 5. Let me explain: Take the number 50, inside the mod 35 ring this is 15. But 50 = 10* 5 = (10 – 7)*5. I was able to pull that modulo 35 stuff on a ring back to modulo 7 stuff on a field…

Another thing I want to remark is that I formulated these new little theorems of Fermat mostly in prime numbers. That makes them more symmetric like the beautiful pair of equations above, but it can be a bit more general like I showed you in the last post using the number 210 that is made up of four different prime factors. And even that is not needed; prime factors can be double or triple it does not matter. As long as the exponent is a prime number my freshly crafted proof will sail you through all the troubles there are.

In a parallel development I found a perfect math professor. It’s a female and she has an amazing career record: At age three already a Fields medal while before she was nine years of age already the third Abel prize for lifetime achievement math… It is surely amazing…;)

But serious, this post is not that long. Only five pictures and like I said above it is not a ‘most general’ kind of proof but it uses a fixed pair of prime numbers. I think it is better this way because if I would formulate all the stuff in a general setting the only people who could understand such a writing are the ones who already figured the stuff out for themselves… Ok, all pictures are in the usual 550×775 pixelf format so here we go:

We are almost at the end: Let me give you one more example as why only in the exponent you need a prime number. We take the number 8 and raise it to the power 5 and do the reducing modulo thing by 40.
Doing so gives that: 8^5 mod 40 = 32768 mod 40 = 32768 – 819*40 = 8.

Ok, that is what I had to say for this post.

A few posts back I used the number 210 to craft seven so called ‘primitive’ counter examples to the famous last theorem of Fermat. Each of those seven primitives can be changed in an infinite number of ways so we have seven streams of counter examples to the last Fermat theorem. It has to be remarked that all counter examples I found since Jan are all based on the so called divisors of zero idea. So if you hear people talking about that in a timespan of 3.5 centuries nobody was able to find counter examples, they are not lying if they mean a counter example on the space of real integers. Yet in Jan this year we observed I had two counter examples using the 3D Gaussian integers, it was one or two days later I found all those counter examples on the spaces of modulo arithmetic.
Beside his so called last theorem Fermat has done a lot more and one of those things is Fermat’s little theorem. To my surprise there are many more variants possible of this little theorem. The little theorem says that for a number a coprime to some prime number p the following holds:
a^p = a mod p. Two numbers are coprime if they share no common factor, if a is a number between 1 and p this is always the case.

The most simple example: a = 2 and p = 3. The little theorem now says that 2^3 mod 3 = 2. This is correct because the remainder of 8 divided by 3 equals 2.

The variants I found can be summarized as next:
2^3 mod 6 = 2 and
3^2 mod 6 = 3.
As you see I take it modulo a composite number. I still do not have a satisfactory proof so for the time being this is a conjecture. I am planning a seperate post for outlining where in my view the problems are that must be proved for the status of conjecture being dropped. So for the time being this is Reinko’s little conjecture.

But can you use a composite number with more than two factors? Yes but you can only use prime numbers in the exponent. Not that it will always fail if you do not use a prime exponent but that is a mathematical story for another day. Anyway this post uses the number 210 because it is the smallest number with four prime factors.
Before we go to the content of this post, to my surprise yesterday I observed a proof that is strikinly similar to the easy way I constructed those counter examples to the last theorem of Fermat. I found it on brilliant.org, here is a link:
https://brilliant.org/wiki/fermats-little-theorem/
Over there they prove the little theorem for a + 1 if it is true for a. Now why do they not use it for finding counter examples to the last theorem of Fermat? Well my dear reader, the human mind is bad at math. We are only monkeys or smart apes if you want, math is something that fascinates our minds but humans are horribly bad at math. Believe me: I am a human myself…;)
Here is a picture from that proof from brilliant dot org:

The whole post is only two pictures long, each of the ususal size of 550×775 pixels. Here we go:

Ok, that was it for this post. Thanks for your attention & see you in the next post.

To my amazement there are many more forms of the so called Fermat little theorem. Fermat’s little theorem uses numbers that are relatively prime to each other (also known as coprime numbers or better: coprime real integers). I hope it is not confusing for you that I write ‘real integers’ but that is meant to make clear these are not Gaussian integers but integers from the real line.
The little theorem of Fermat has some generalizations like the Euler theorem and a person named Carmichael also worked on stuff like that. Yet the coprime stuff is always assumed while the results I found last week do not need that at all. But I do need prime numbers in the exponent, that’s all.
When I found those counter examples to Fermat’s last theorem about 3 months back I was amazed I could find nothing of that on the entire internet. Ok my first stuff was done with 3D complex & circular Gaussian integers so that is logical nobody else writes about that. But that expressions like 5^n + 7^n = 12^n modulo 35 is something that baffled my mind. This is so simple to prove that it is hard to understand why this is not a standard counter example to the last theorem of Fermat. To refresh your mind: the last theorem of Fermat says there exists no integers such that x^n + y^n = z^n for n > 2. This has been an open problem for about 3.5 centuries of time, it was solved by Andrew Wiles in the beginning of the nineties of the last century but even Andrew never mentions those easy to craft counter examples to the last theorem of Fermat.

A paradox.
The last theorem of Fermat was unproven for centuries. But the far more easy little theorem of Fermat was proven rather quick and that proof is very easy compared to the Andrew Wiles thing. Now I am having the opposite problem: The counter examples to Fermat’s last theorem are so simple to construct that in the beginning I was hesitant to use it all. While for these new variants of the little theorem of Fermat, I do not know how to prove that. So my stuff is more or less opposite to the historical developments as they are known; that is why I consider this a little paradox.

In this post I formulate a few easy to understand variants of the little theorem of Fermat. In this post I choose to do it as symmetrical as possible like in the next pair:
7^11 = 7 modulo 77 &
11^7 = 11 modulo 77.
As you see on inspection; these are clearly variants of the little theorem but the exponents and the 77 of the modulo thing are not coprime. For myself speaking I consider the above pair as an example of ‘mathematical beauty’. Of course it is hard to give a definition of ‘math beauty’, you recognize it when you see it but it is hard to define because beauty itself is not a mathematical object or so.

Anyway beautiful or ugly as a math professor, this post is six pictures long all in the standard format of 550×775 pixels. Here we go with the picture stuff:

A few posts back I crafted seven counter examples to the last theorem of Fermat and those were based on the number 210. Actually each of those seven ‘primitives’ gave rise to an infinite series of counter examples so that the overpaid math professors once more know their contribution to this all: ZERO!
But you can make four new little Fermat theorems using the number 210 so may be that is the next post. On the other hand the USA based Fermilab has all kinds of new results out upon the muon and they keep on thinking that elementary particles like electrons and muons are magnetic dipoles. Instead of offering some fundamental proof for the magnetic dipole nature of electrons we only get a complicated story that, as usual, neglects that electrons and muons get accelerated by magnetic fields.

So I don’t know about the next post. Well thanks for your attention, have a healthy life and ruthlessly kill all math professors. Or may be not…;)