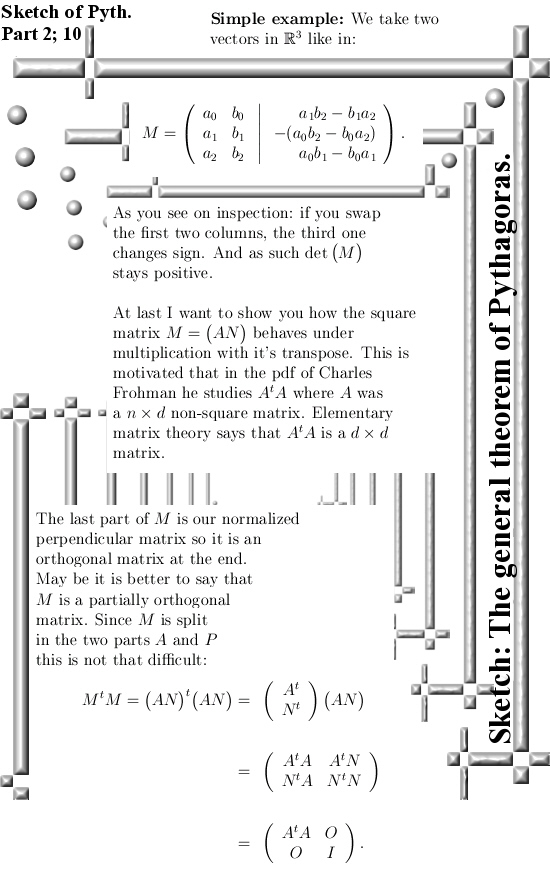
The reason I name these two posts a sketch of (a proof) of the full theorem of Pythagoras is that I want to leave out all the hardcore technical details. After all it should be a bit readable and this is not a hardcore technical report or so. Beside this, making those extra matrix columns until you have a square matrix is so simple to understand: It is just not possible this method does not return the volume of those parallelepiped.
I added four more pictures to this sketch, that should cover more or less what I skipped in the previous post. For example we start with a non-square matrix A, turn it into a square matrix M and this matrix M always has a non-negative determinant. But in many introductionary courses on linear algebra you are thought that if you swap two columns in a matrix, the determinant changes sign. So why does this not happen here? Well if you swap two columns in the parallelepiped A, the newly added columns to make it a square matrix change too. So the determinant always keeps on returning the positive value of the volume of any parallelepiped A. (I never mentioned that all columns of A must be lineary independent, but that is logical we only look at stuff with a non-zero volume.)
Just an hour ago I found another pdf on the Pythagoras stuff and the author Melvin Fitting has also found the extension of the cross product to higher dimensions. At the end of this post you can view his pdf.
Now what all these proof of the diverse versions of Pythagorean theorems have in common is that you have some object, say a simplex or a parallelepiped, these proof always need the technical details that come with such an object. But a few posts back when I wrote on it for the first time I remarked that those projections of a parallelogram in 3D space always make it shrink by a constant factor. See the post ‘Is this the most simple proof ever?’ for the details. And there it simply worked for all objects you have as long as they are flat. May be in a next post we will work that out for the matrix version of the Pythagoras stuff.
Ok, four more pictures as a supplement to the first part. I am to lazy to repair it but this is picture number 8 and not number 12:



Ok, lets hope the pdf is downloadable:
That was it for this post. Thanks for your attention.