Category Archives: Laplacian

Factorization of the Laplacian (for 2D, 3D and 4D complex numbers).

December 7, 20203D complex numbers, 4D complex numbers, CR equations, Laplacian, Magnetism, Quantum mechanicsReinkoVenema

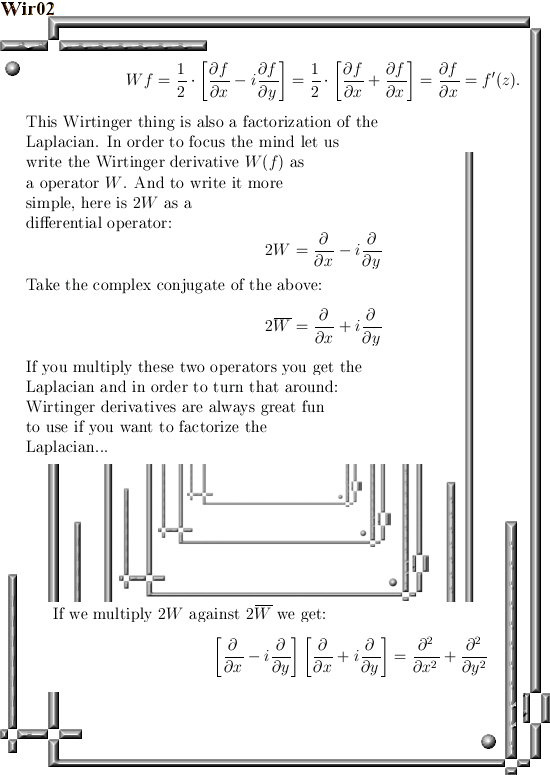
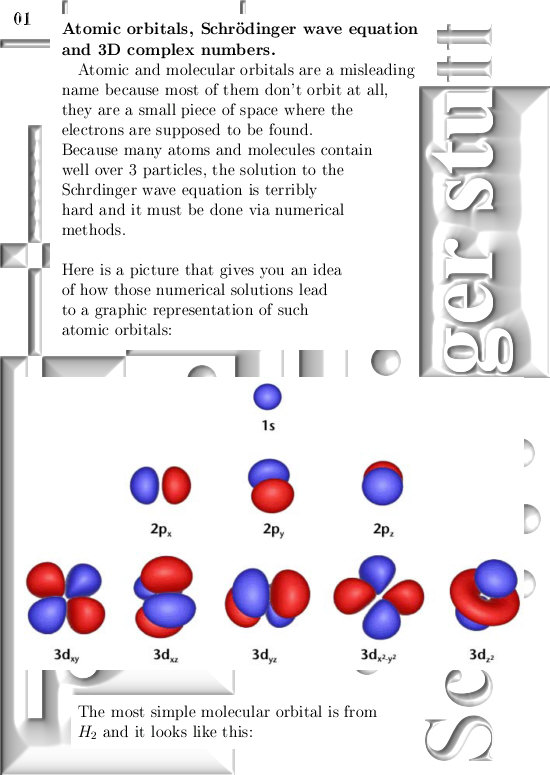
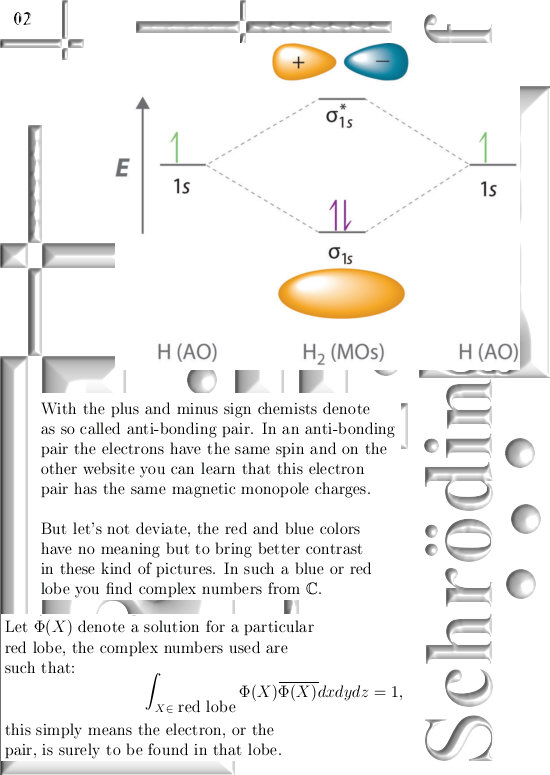
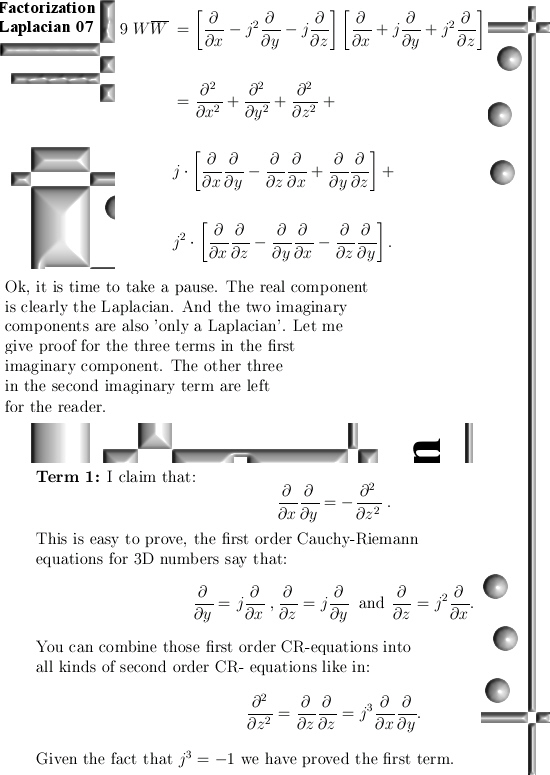
Originally I wanted to make an oversight of all ways the so called Dirac quantization condition is represented. That is why in the beginning of this post below you can find some stuff on the Dirac equation and the four solutions that come with that equation. Anyway, Paul Dirac once managed to factorize the Laplacian operator, that was needed because the Laplacian is part of the Schrödinger equation that gives the desired wave functions in quantum mechanics. Well I had done that too once upon a time in a long long past and I remembered that the outcome was highly surprising. As a matter of fact I consider this one of the deeper secrets of the higher dimensional complex numbers. Now I use a so called Wirtinger derivative; for example on the space of 3D complex numbers you take the partial derivatives into the x, y and z direction and from those three partial derivatives you make the derivative. And once you have that, if you feed it a function you simply get the derivative of such a function.

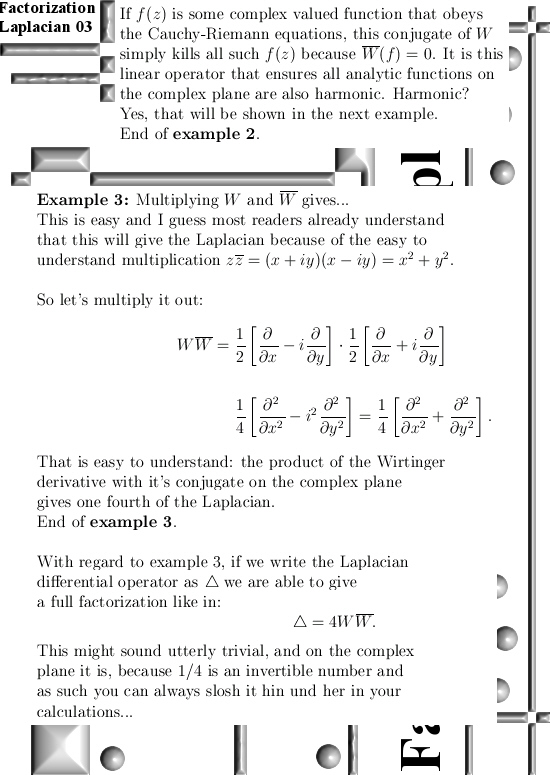
Now such a Wirtinger derivative also has a conjugate and the surprising result is that if you multiply such a Wirtinger derivative against it’s conjugate you always get either the Laplacian or in the case of the 3D complex numbers you get the Laplacian multiplied by the famous number alpha.

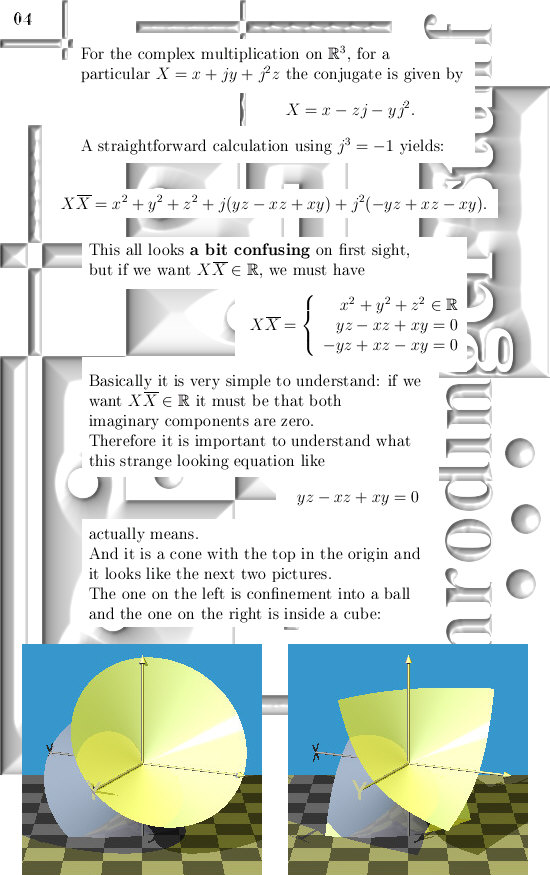
That is a surprising result because if you multiply an ordinary 3D number X against it’s conjugate you get the equation of a sphere and a cone like thing. But if you do it with parital differential operators you can always rewrite it into pure Laplacians so there the cones and spheres are the same things…

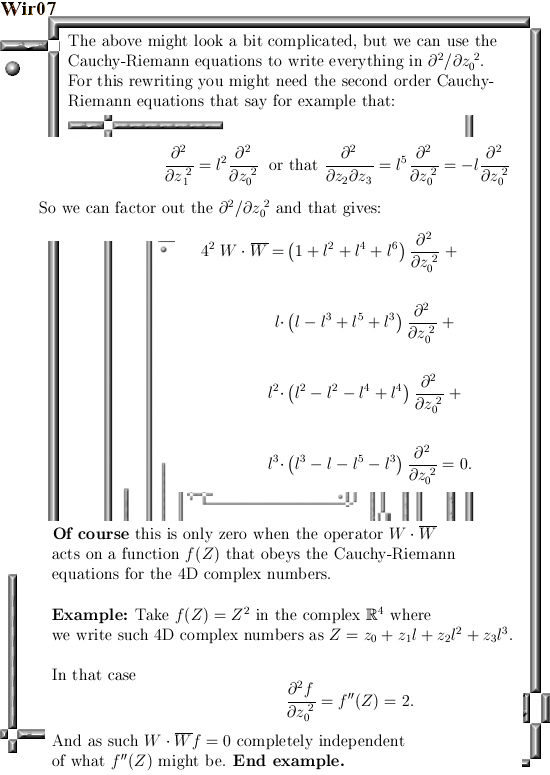
In the past I only had it done on the space of 3D numbers so I checked it for the 4D complex numbers and in about 10 minutes of time I found out it also works on the space of 4D complex numbers. So I started writing this post and since I wanted to build it slowly up from 2D to 4D complex numbers it grew longer than expected. All in all this post is 15 pictures long and given the fact that people at present day do not have those long timespan of attention anymore, may be it is too long. I too have this fault, if you hang out on the preprint archive there is just so much material that often after only five minutes of reading you already go to another article. If the article is lucky, at best it gets saved to my hard disk and if the article has more luck in some future date I will read it again. For example in the year 2015 I saved an article that gave an oversight about the Dirac quantization condition and only now in 2020 I looked at it again…

The structure of this post is utterly simple: On every complex space (2D, 3D and 4D) I just give three examples. The examples are named example 1, 2 and not surprising I hope, example 3. These example are the same, only the underlying space of complex numbers varies. In each example number 1 I define the Wirtinger derivative, in example 2 I take the conjugate while in the third example on each space I multiply these two operators and rewrite the stuff into Laplacians. The reason this post is 15 pictures long lies in the fact that the more dimensions you have in your complex numbers the longer the calculations get. So it goes from rather short in the complex plane (the 2D complex numbers) to rather lengthy in the space of 4D complex numbers.

At last I would like to remark that those four simultanious solutions to the Dirac equation it once more shouts at your face: electrons carry magnetic charge and they are ot magnetic dipoles! All that stuff like the Pauli matrices where Dirac did build his stuff upon is sheer difficult nonsense: the interaction of electron spin with a magnetic field does not go that way. The only reason people in the 21-th century think it has some merits is because it is so complicated and people just loose oversight and do not see that it is bogus shit from the beginning till the end. Just like the math professors that neatly keep themselves stupid by not willing to talk about 3D complex numbers. Well we live in a free world and there are no laws against being stupid I just guess.

Enough of the blah blah blah, below are the 15 pictures. And in case you have never ever heard about a thing known as the Wirtinger derivative, try to understand it and may be come back in five or ten years so you can learn a bit more…
As usual all pictures are 550×775 pixels in size.

Oh oh the human mind and learning new things. If a human brain learns new things like Cauchy-Riemann equations or the above factoriztion of the Laplacian, a lot of chages happen in the brain tissue. And it makes you tired and you need to sleep…
And when you wake up, a lot of people look at their phone and may be it says: Wanna see those new pictures of Miley Cyrus showing her titties? And all your new learned things turn into insignificance because in the morning what is more important compared to Miley her titties?

Ok my dear reader, you are at the end of this post. See you in the next post.

Three video’s to kill the time.

December 1, 2020Laplacian, MagnetismReinkoVenema

Orginally I wanted to include some video in the previous post that serves as a teaser post for the impending factorization of the Laplacian for 2D, 3D and 4D complex numbers. But it was already late at night and only adding one video made the post look like it is just as chaotic as I always am…;)

So let’s get started with video number 1: Goodbye Determinism, Hello Heisenberg Uncertainty Principle from Irvin Ash. This Irvin guy is one of those professional Youtubbers that apearently can make money by throwing out a lot of video’s. In his case it is often physics and in my view he only repeats what he has read or seen in other video’s. There is not much original thinking in but hey Irvin can make a buck and it keeps him busy.

But in one of the video’s he is making such a strange mistake, it is so stupid that it is unbelievable. It is like stating that 1 + 1 = 3 or like 1 – (-1) = 0. Some mistakes or faults are so trivial that no matter what your own brain instantly recognizes something is going wrong. In this case Irvin explains the double slit experiment and his explanation for the first place where interference disappears is that they are out of phase by one wavelength… I wonder how you can make such a mistake without your own brain instantly jumping in with ‘that is not right’.

I also made a nice cube from the above screen shot:

I think I was 16 when we had to do such calculations…

And finally the video itself:

The second video is from Sabine Hossenfelder. Unlike Irvin Sabine has a lot of original thinking to share and as such she is a far cry from a talking book like Irvin Ash. In her video she explains how medical magnetic resonance devices work. Back in the time when I figered out that it is just not logical on all kinds of levels that electrons and other spin half particles are magnetic dipoles, for me it was important to find alternative explanations for things like MRI devices. In physics it is well known that accelerating electrons and protons give off electro-magnetic radiation, if there is zero acceleration no radiation is emmited. So the explanation as given in the video cannot be right, it is about magnetic moments that start spinning round and ‘therefore’ give off radiation. Problem with this is: there is no real acceleration so what explains the emitted radiation?

If protons and electrons carry magnetic charge, that is they are magnetic monopoles, all of a sudden there is room for acceleration and as such you can observe those resonance frequencies. Compare it to a music intrument: if you have a guitar with zero tension on the wires, it will never produce any sound let alone some cute music. In MRI scans there is also a static magnetic field, only when the protons and electrons are magnetic monopoles this ‘brings the tension’ needed for the resonance to work in the first place. Sorry Sabine, your version of physical reality has a lot of holes in it because it is based on the Gauss law for magetism and that law says that no magnetic monopoles exist…

You explanation does not carve any wood Sabine; why is the static magnetic field needed?

In case you never dived into the niceties of MRI scanners, please see the video. And don’t forget to be a bit critical: if protons are really magnetic dipoles, then what the fuck is that static magnetic field doing? But if protons (and electrons) carry magnetic charge all of a sudden things become logical. Not that I expect during my lifetime only one of the professional physics professors to say that I am in the right, but there is no use in getting emotional. All I do is repeating the nonsense that goes on as accepted common knowledge while it is retarded: If a proton has two magnetic poles then why do you need the static magnetic field?

The third video is about how Paul Dirac succeeded into factorizing the Laplacian differential operator. It is far different from how I managed to do that; I used so called Wirtinger derivatives and multiply those against their conjugate and voila: there is your factorization. No, Paul Dirac used 4×4 matrices that anti-commute and as such he was able to get rid of a nasty square root. Phyics people go totally bonkers on that calculation, I do not. Not that I do not like it, but Paul made the mistake of basing his matrices on the Pauli matrices for electron spin. And the Pauli matrices can’t be correct because it is based on the flawed idea that electrons are magnetic dipoles.

There is a funny anecdote going round about Paul Dirac. It says: There is no God and Dirac is his prophet. But serious: If electrons were magnetic dipoles you instantly run into dozens of weird problems. Like permanent magnets, of they are explained by the spins of the electrons aligning themselves and just as if you have a bunch of tiny magnets they will form a large permanent one. But in chemistry and electron pair with the same spin is known as an anti-binding electron pair. How can in permanent magnets the alignment of electrons enforce each other while in chemistry that causes a non-binding electron pair? Once more: I only use logic. It is logical that electrons, protons and neutrons carry net magnetic charge and as such are always magnetic monopoles.

Enough of the blah blah blah, here is the last video of this post:

At last a ‘cube picture’ for the Dirac thing:

Ok, that was all I had to day. Thanks for your attention and don’t forget to turn enough math professors into bio-diesel. Everybody knows that bio-diesel made from math professors is the finest quality there is on this entire earth… So good luck with the hunt for math professors…;)

Teaser for the next post on Wirtinger derivatives.

December 1, 20204D complex numbers, Exponential circle, Laplacian, MagnetismReinkoVenema

Man oh man, the previous post was from 12 Nov so time flies like crazy. Originally I wanted to write a post on a thing you can look up for yourself: the Dirac quantization condition. I have an old pdf about that and it says that it was related to the exponential circle on the complex plane. Although the pdf is from the preprint archive, it is badly written and contains a ton of typo’s and on top of it: the way the Dirac quantization is formulated is nowhere to be found back on the entire internet. In the exponent of the exponential circle there is iqg where q represents an elementary electric charge and g is the magnetic monopole charge according to Paul Dirac. Needless to say I was freaked out by this because I know a lot about exponential curves but all in all the pdf is written & composed so badly I decided not to use it.

After all when I say that electrons carry magnetic charge and do not have bipolar magnetic spin, the majority of professional physics professors will consider this a very good joke. And if I come along with a pdf with plenty of typo’s the professional professors will view that as a validation that I am the one who has cognitive problems and of course they are the fundamental wisecracks when it comes to understandig electron spin. Our Pauli and Dirac matrices are superior math, in the timespan of a hundred years nothing has come close to it they will say.

Here is a screen shot of what freaked me out:

Furthermore I was surprised that the so called professional physics professors have studied stuff like ‘dyons’. So not only a Dirac magnetic monopole (without an electric charge but only a magnetic charge), a dyon is a theoretical particle that has both electric and magnetic charge. But hey Reinko, isn’t that what you think of the electron? There are two kinds of electrons, all electrons have the same electric charge but the magnetic charge comes in two variants.
There are so many problems with the idea that electrons are magnetic dipoles, but the profs if you give them a fat salary will talk nonsense like they are a banker in the year 2007.

So I decided to skip the whole Dirac quantization stuff and instead focus a bit on factorizing the Laplacian differential operator. I the past I have written about that a little bit, so why not throw in a Google search because after all I am so superior that without doubt my results will be found on page 1 of such a Google search! In reality it was all ‘Dirac this’ and ‘Dirac that’ when it comes to factorization of the Laplacian on page 1 of the Google search. So I understood the physics professors have a serious blockade in their brains because this Dirac factorization is only based on some weird matrices that anti-commute. These are the Pauli and Dirac matrices and it is cute math but has zero relation to physical reality like the electron pairs that keep your body together.

No more of the Dirac nonsense! I sat down and wrote the factorization of the Laplacian for 4D complex numbers on a sheet of paper. Let me skip all this nonsense of Dirac and those professional physics professors and bring some clarity into the factorization of the Laplacian.
It took at most 10 minutes of time, it is just one sheet of paper with the factorization. I hope this is readable:

So that is what I have been doing since 12 April, since the last post on this website. I have worked my way through the 2D complex plane, the 3D complex numbers and finally I will write down what did cost me only 10 minutes of time a few weeks ago…

In a few days the post wil be ready, may be this week. If not next week & in the meantime you are invited to think about eletrons and why it is not possible that they are magnetic dipoles.

See you in the next post.

Part 8 of the 4D basics: Wirtinger derivatives.

July 4, 20184D complex numbers, CR equations, LaplacianReinkoVenema

This is the 91-th post on this website so surely but slowly this website is growing on. This post was more or less written just for myself; I don’t know if the concept of Wirtinger derivates is used a lot in standard complex analysis but I sure like it so that’s why we take a look at it.

The idea of a Wirtinger derivative is very simple to understand: You have some function f(Z) and by differentiating it in the direction of all four basis vectors you craft the derivative f'(Z) from that.

At the basis for all the calculations we do in this post are the Cauchy-Riemann equations that allow you to rewrite the partial derivatives we put into the Wirtinger derivative.

The main result in this post is as follows:
We take our Wirtinger operator W and we multiply it with the 4D complex conjugate of W and we show that this is a real multiple of the Laplacian.

The 4D case is more or less the same as on the complex plane, that is not a miracle because in previous 4D basics we already observed two planes inside the 4D complex numbers that are isomorphic to the complex plane. So it is not much of a surprise the entire 4D space of complex numbers behaves in that way too; all functions are harmonic that is the Laplacian of such a function is zero.

This post is ten pictures long, most of them are size 550 x 775 but a few of them are a bit broader like 600 x 775 because the calculations are rather wide.

On the scale of things this post is not ultra important or so, it is more like I wrote it for myself and I wanted to look in how much this all was different from the three dimensional case.

Here are the pics:

Further reading from a wiki (of course that is only about 2D complex numbers from the complex plane):
Wirtinger derivatives
https://en.wikipedia.org/wiki/Wirtinger_derivatives

Ok, that was it. Till updates.

Wirtinger derivatives and the factorization of the Laplacian.

August 5, 20163D complex numbers, CR equations, Laplacian, Quantum mechanicsReinkoVenema

This post could have many titles, for example ‘Factorization of the Laplacian using second order Cauchy-Riemann equations’ would also cover what we will read in the next seven pictures.

The calculation as shown below is, as far as I am concerned, definitely in the top ten of results relating to all things 3D complex numbers. Only when I stumbled on this a few years back I finally understood the importance of the so called sphere-cone equation.

The calculation below is basically what you do when writing out the sphere-cone equation only now it is not with variables like x, y and z but with the partial differential operators with respect to x, y and z. In simplifying the expressions we get I use so called second order Cauchy-Riemann equations, if you understand the standard CR equations these second order equations are relatively easy to digest.

Have fun reading it.

This post is also categorized under Quantum Mechanics, the reason for that is that the wave equation contains the Laplacian operator and the more you know about that rather abstract thing the better it is in my view.

I would like to close with a link to a wiki on Wirtinger derivatives, originally they come from theory with several complex variables. That explains why in the wiki the Wirtinger derivatives are written as partial derivatives while above we can use the straight d´s for our differential of f.

Here is the wiki: Wirtinger derivatives
https://en.wikipedia.org/wiki/Wirtinger_derivatives

Till updates.

Schrödinger wave equation part 2.

April 1, 20163D complex numbers, Laplacian, Quantum mechanicsReinkoVenema

A few posts back I wrote a bit about the Schrödinger wave equation related to calculating atomic and molecular orbitals for electrons using 3D complex numbers.

What I said was basically correct but also an over-simplification of the situation.
The problem is very very basic: in the 3D number system, let it be complex or circular, you just cannot solve and equation like $X^2 = -1$.
Hence the number i from the complex plane with i^2 = -1 just does not live in 3D real space.

So using alternative number systems outside the complex plane is not a straightforward thing to do, yet in principle all higher dimensional complex numbers should give the same results.
If not there would be a very basic problem inside the wave equation from quantum mechanics and I am not aware of any faults in that detail of the quantum theory.

Here are two pictures that serve as an addendum on the previous post on the Schrödinger equation:

Now if you are reading this it is very likely that at least once in your life you have seen a solution to the Schrödinger wave equation like the ‘particle in a box’. And that is not a 3D box but the one dimensional box or just an interval of the real line.

Solving the Schródinger stuff for atomic and molecular orbitals is a very different kind of game; these are always many particle systems where every particle influences the system and the entire system influence the individual particles.
Mathematically speaking it is a nightmare; analytical solutions are not possible they say.
It can only be solved numerically…

__________

But keep on dreaming, after all they also say decade in decade out that electrons are magnetic dipoles. There is no experimental proof for that only theoretical bla bla bla.

Let’s leave it with that. Till updates.

Atomic orbitals, the Schrödinger wave equation and 3D complex numbers.

February 29, 20163D complex numbers, Exponential circle, Laplacian, Quantum mechanicsReinkoVenema

The numerical use of three dimensional complex numbers is almost the same as the situation on the complex plane. This is caused by the simple fact that only on the main cone that includes the three coordinate axes, we have that if you multiply a number X by it’s conjugate, the result is a real number.

In the complex plane this is valid for all numbers in the plane but in higher dimensional complex number systems the situation is different; you must always pick numbers from that main cone where also the exponential circle lives (in 3D) or exponential curves (in higher dimensions).

This update is 5 pictures long, size pics = 550 by 775.

__________

One hour later:

Shit! There is a serious problem with uploading the pictures, they get uploaded but they are not visible… So you must wait at least one day longer because I do not understand the problem at hand…

Till updates.

__________

Problem with the jgp pictures is solved; according to my webhost provider it was caused by the name Schrödinger because that contains an o with two dots: ö.
My computer can handle filenames with ö so for me they looked normal but the server that hosts this website cannot deal with these kinds of symbols…

Anyway after a few days here are the pictures:

Well I am happy this strange problem of invisible pictures has been solved. Till updates.

Seven properties of the number alpha.

February 9, 20163D complex numbers, Laplacian, Matrix representationReinkoVenema

The number alpha is one of my best finds in the field of mathematics. In all kinds of strange ways it connects very different parts of math to one another, for example when it comes to partial differential equations the number alpha plays a crucial role in transforming this of a pile of difficult stuff into something that lives in only one dimension.

You can also use the number alpha for perpendicular projections, you can use it for this and you can use it for that.

__________

Now in the previous post I told you I would write out some of the elementary properties of the number alpha, but when I finished it the thing was about 5 A4 size pages long and that would be about 10 pictures on this new website.

That would be a bit too long and also I had written nothing in the page for 2016 on the other website. So I decided to hang those five A4 pages in the old website and you get a few teaser pictures on this new website.

Here are the three teaser pictures, click on any to land on the alpha update:

The applet I used is a very helpfull tool, you can find it here:
http://calculator.vhex.net/calculator/linear-algebra/matrix-exponential-using-the-pade-approximation

Ok, that was it. Till updates and do not forget to floss your brain a bit every now and then…

Calculating the Laplacian using the Cauchy-Riemann equations.

January 30, 20163D complex numbers, CR equations, LaplacianReinkoVenema

Without doubt the Laplacian is a very important differential operator. It plays a major role in for example the classical wave equation and also the Schrödinger wave equation from quantum mechanics.

Now scroll a bit back until you find the post on the Cauchy-Riemann equations, at the end I used the phrase ‘Cauchy-Riemann equations chain rule style’ and this is how we can crack in a very easy way how the Laplacian operates on functions that obey the CR equations on 3D complex numbers.

I have hundreds and hundreds of pages of math stuff on the 3D complex number system and very often I use the number alpha. This number alpha is so important, not only in 3D, that it is worth to post a few posts on them.

For the time being, I just conducted a simple Google search on the phrase ‘3d complex numbers’ in the search detail for pictures. And every time this old teaser picture from the other website pops up:

At the end you see that (1, -1, 1), well that is three times alpha.

It is a nice exercise to prove that the square of alpha equals alpha.
So alpha is in the same category as for example numbers like 0 and 1 because if you square those you also get the original number back in return.

After all one squared equals one and zero squared equals zero.

End of this update, till updates.

3Dcomplexnumbers

Math as you have never seen before…

Category Archives: Laplacian

Factorization of the Laplacian (for 2D, 3D and 4D complex numbers).

Three video’s to kill the time.

Teaser for the next post on Wirtinger derivatives.

Part 8 of the 4D basics: Wirtinger derivatives.

Wirtinger derivatives and the factorization of the Laplacian.

Schrödinger wave equation part 2.

Atomic orbitals, the Schrödinger wave equation and 3D complex numbers.

Seven properties of the number alpha.

Calculating the Laplacian using the Cauchy-Riemann equations.