This post is based on a video from Dr. Brant Carlson who is talking about a spin half particle in a magnetic field. I have selected this video because Mr. Carlson is rather good at explaining the stuff so although I hefty disagree with most of his conclusions this post should not be viewed as some kind of character attack on Mr. Carlson.
Let me first give you the video, you can watch it now or later.
Spin 1/2 in a B field:
This post is just about two details;
1) Is electron spin conserved yes or no?
2) The lack of insight Mr. Carlson shows while discussing the Stern-Gerlach experiment.
Let’s start with 1) Is electron spin conserved?
If you read some wiki’s about the Stern-Gerlach experiment you often come across the repeated measurements of electron spin. There are of course infinitely many ways to measure electron spin if it were a vector but the professionals only do it in three directions known as x, y and z.
It is important to never forget all those measurements are done during the application of a vertical magnetic field, the vertical magnetic field is there all the time and within that boundary condition they derive the properties of the spin operators that measure spin into the x and y axis directions.
When you read about the Stern-Gerlach experiment it is often stated that if you measure spin in the vertical direction, half of the electrons go up and the other half go down.
If after that you make a measurement into the x or y direction of the up electrons, once more the beam of electrons will split 50/50.
If after that you make a new z-axis direction measurement, once more it will split into 50% up and 50% down states of the electron.
To put it simple: There can not be conservation of electron spin if a second measurement rams half of the electrons into another spin state… Anyway this is what the official generally accepted knowledge strongly suggests: if changing the applied magnetic field pushes electrons out of their previous state it looks like there is no conservation of electron spin.
From the beginning of the video in the next picture you see the so called Pauli matrices and the two Pauli matrices for the x and y direction have interesting eigenvectors:
These eigenvectors suggest a super position of the two eigenvectors into the z-axis direction and very important:
If you square the probability amplitudes you always get 50%.
This is a theoretical result, I have never found any experimental proof validating these theoretical considerations. Here is the picture that is a screen shot from the beginning of the video:
So if Sz is already measured, suppose it is plus h bar over 2, if after that Sx is measured and it is minus h bar over 2, is spin conserved?
I would say no, but I think the electron has one of two possible magnetic charges and with charge it does not matter in what kind of direction you measure it.
The professional physics professors think that electron spin in the z-axis direction is independent of any direction perpendicular to the z-axis direction. So they will argue that it is irrelevant what the outcome of Sx is because the spin in the z-axis direction will be conserved because it is angular momentum…
As I see it, repeated measurement of electron spin in orthogonal directions should always give the same result. But there are serious problems with an experiment like that:
1) It should be done inside a cage of Faraday because em-radiation reacts with the electrons, 2) It should be done in a vacuum because the electron beam should not interfere with the electrons in the air molecules.
If done properly, in my view you should always measure the same spin for the electron.
So far the pondering if electron spin is conserved, one thing is clear: the last word is not spoken on that detail.
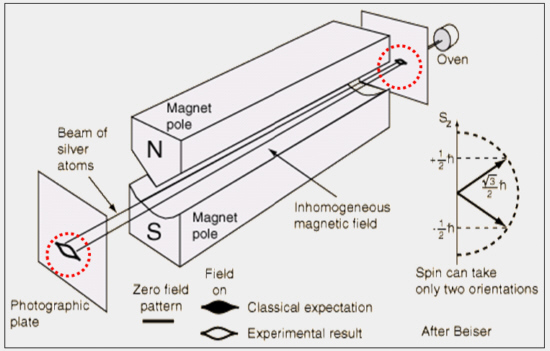
Detail 2 is about the staggering lack of insight Mr. Carlson shows upon that very important experiment: the Stern-Gerlach experiment. The weird thing in this experiment is the fact that half of the unpaired electrons go into the direction of the stronger part of the inhomogeneous magnetic field while the other half goes into the direction of the weaker part.
When I first learned about the SG experiment I was completely puzzled by the fact the electron went into the direction of the weaker part of the magnetic field.
Here is a picture of the Stern-Gerlach experiment, one of the faults that so many physics people expose is that it are ‘silver atoms’. But it is silver vapour and that is over 2000 degrees Celsius. Also silver is a diamagnetic material; at present day we know that if a metal has no unpaired electrons it is diamagnetic and as such repels magnetic fields very weakly… (Cute detail: the electron pairs in a diamagnetic material start to spin in such a way that the outside magnetic field is partly offset, but it does not fade away and as such the spinning electron pair is the smallest scale super conductivity possible. Even at room temperature…)
By the way, silver has 47 protons so there should be one unpaired electron in a neutral silver atom.
One of the problems with electrons being a magnetic dipole is that the electron pair is also a magnetic dipole but there are huge differences between the behaviour of diamagnetic materials (containing only electron pairs) and para & ferro magnetic materials that have unpaired electrons.
Since in the original Stern-Gerlach experiment the beam of silver ions was split in 2 we can conclude that it is likely that only one unpaired electron was responsible for this to happen. To understand the result a bit; the nucleus of a silver atom or ion is about 108 thus 47 protons and 61 neutrons. Different isotopes might have another number of neutrons but anyway: the protons is about 1800+ times as heavy as the electron so one unpaired electron moves the mass of a silver nucleus that is about 108 times 1800 or about 200 thousand times the mass of the electron.
Now why should electrons move to the weaker part of the applied magnetic field?
You always hear explanations like the Larmor frequency that makes the electrons that are anti aligned with the applied magnetic field that prevent them from alignment with the magnetic field.
I think that these Larmor frequencies are much more like a tiny ball on an elastic string, just like electrons can vibrate under the application of an electric field.
If true, in my view only electrons that are part of an atom/molecule or ion will produce this so called Larmor frequency while if you put a magnetic field on a plasma nothing will happen…
Here is a nice picture of some stuff with spin 5/2, that means there are five unpaired electrons. By the way, did you notice that the official professional professors just add up the electron spin like it is a charge and not a vector?
But the official theory says electron spin should be viewed as a tiny vector…
Anyway, in the picture you see that as the applied magnetic field increases one by one the electrons start vibrating. In my view this suggests that at a particular strength of the B field the electron comes loose and vibrates a short time as a tiny ball on an elastic string.
Source of this lovely picture: Electron Paramagnetic Resonance EPR
http://encyclopedia2.thefreedictionary.com/Electron+Paramagnetic+Resonance+EPR
The main problem is still not solved: Why do the electrons in the Stern-Gerlach experiment go into the direction of the weaker parts of the inhomogeneous magnetic field???
Why do these magnetic dipoles not turn in order to get attracted by the stronger parts of the magnetic field?
In my view this is because the electron is not a magnetic dipole but a particle that carries a north or a south magnetic charge.
How does Dr. Brant Carlson explain this very strange behaviour of the unpaired electron?
From the video of Dr. Carlson we observe that for inhomogeneous magnetic fields the classical way of calculating the force on a (macroscopic) magnet is given by:
This is easy to understand: The mu is the dipole moment of lets say a bar magnet, B is the applied external magnetic field. If I remember it correctly you should take the inner product against the gradient of B but let not put salt on all snails.
With the above mechanism Dr. Brant wants to explain as why just one electron can pull an entire silver ion from it’s original trajectory. But an electron is very very tiny, it is about 10 to the minus 15 in size. Let us give Dr. Brant the benefit of doubt and suppose the dipole distance in the electron is 10 times the size of the electron or 10 to the power minus 14.
This tiny distance gives rise to almost no difference in magnetic field strength yet the lonely unpaired electron moves the silver ion that is about 200 thousand time as heavy as the electron is.
May be the professional physics professors believe this, but I don’t.
The electron is just too small to give a significant change in the path of the silver ion…
At 28 minutes and 55 seconds in the video I completely loose the line of reasoning as done by Dr. Carlson; we only see some blah blah blah with exponential circles from the complex plane while the main problem that the tiny electron makes a significant change in the path of the silver ion is completely skipped.
Here is scientific disaster in a small screenshot:
Also in this point in time in the video Dr. Brant Carlson mentions the spins into the x and y directions; he claims that the spin relaxation into those directions is so short lived that it does not have any influence…
According to how I view the magnetic stuff as being a charge on the electron, it does not matter if the electron goes through a homogeneous magnetic field or some erratic inhomogeneous magnetic field. If the electron carries a south magnetic charge it will always be attracted to the north pole of the applied magnetic field.
So that is answer 1 to the four questions our brave Dr. Carlson is asking us at the end of this video:
Yeah yeah, check your understanding…
__________
In the next part of this post we are going to use the formula for the force on a magnetic dipole in a non-uniform magnetic field as given by Dr. Brant Carlson above. In order to keep stuff as simple as possible I will multiply the magnetic moment of the electron against the gradient of the magnetic field while demanding the electrons are accelerated with a speed of 1 meter per second every second.
The conclusion is relatively staggering: The gradient of the applied magnetic field must be about five million Tesla in order to get only 10% of the gravitational force on the electron.
It becomes even more staggering if you remark that in the original Stern-Gerlach experiment the moved silver ions are about 200 thousand times as heavy as one unpaired electron. So the applied magnetic field should be also about 200 thousand times as big giving something that likely is not living inside this universe.
Technical details:
1) I used an electron size of 10 to the power -15 meter and
2) I used a dipole magnetic field around the electron that is 10 times as long so 10 to the power -14 meter.
If you do that, the outcome is a staggering gradient of 5 million Tesla per meter so one thing is very very clear: The acceleration as observed in the original Stern-Gerlach experiment from the year 1922 cannot explained by using an unpaired electron having a bipolar magnetic field…
The whole calculation is just two pictures long:
The conclusion is majestic:
If we want the electron to have only an acceleration of one tenth of the earth gravity field while using electron dimensions 10 to the minus 15 and the magnetic field of the electron about 10 times as bit, in that case you need the extreme gradient of five million Tesla per meter…
I was very amazed by this result I found three days back, but I checked and checked my calculations, did I do something wrong or so? Yet I cannot find any fault, furthermore we have to take into account that the professional physics people like Dr. Brant Carlson and thousands and thousands of this colleagues never ever show a calculation like this.
Five million Tesla is so far off the scale, here on earth the strong magnetic field as for example used in MRI scanning in hospitals are about 3 to at most 6 Tesla. We can safely conclude that the acceleration of electrons by magnetic fields in not caused by the supposed electron dipole moment.
For myself speaking I am glad I finally did this easy calculation and I have to thank Dr. Brant Carlson for making this video as shown above because that detail made me irritated enough to finally make the calculation. I am always a bit hesitant when it comes to physical calculation because they are not my first nature, math is often much more simple to me while with physics you also have to keep an eye if your SI units fit properly and so on.
The word count of this post is now over 2200 words, most of the time I try to limit the word count of a post to about 500 words so this is a very long post relative to that.
Lets call it the end and till updates my dear reader.