Category Archives: 2D multiplications

A de Moivre identiy for the i^2 = -1 + i multiplication.

2D multiplications

We already have found some parametrizations for the complex exponential (that ellipse, see previous posts below) we do not really need such an identity. But they are always fun to make such identities in a new number system under study like lately those elliptical and hyperbolic multiplications in the plane.
Lets recap what we have done all these posts:

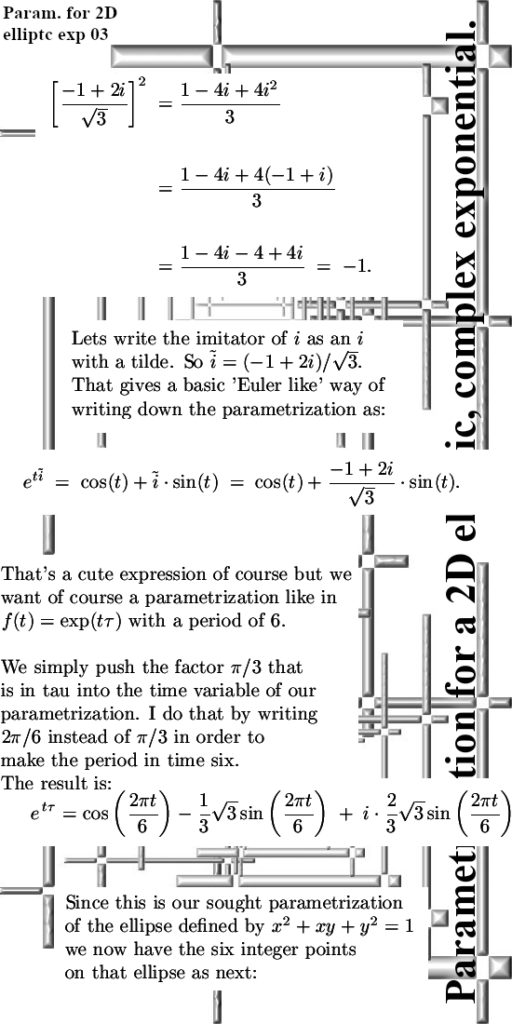
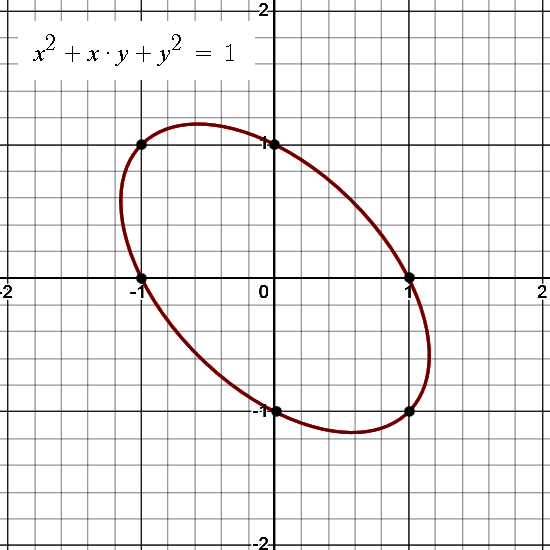
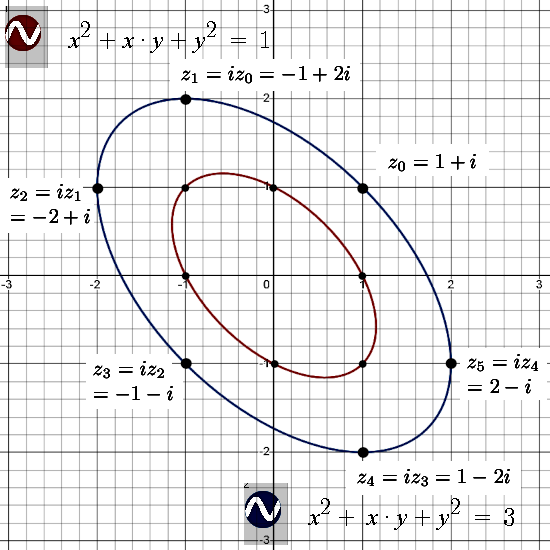
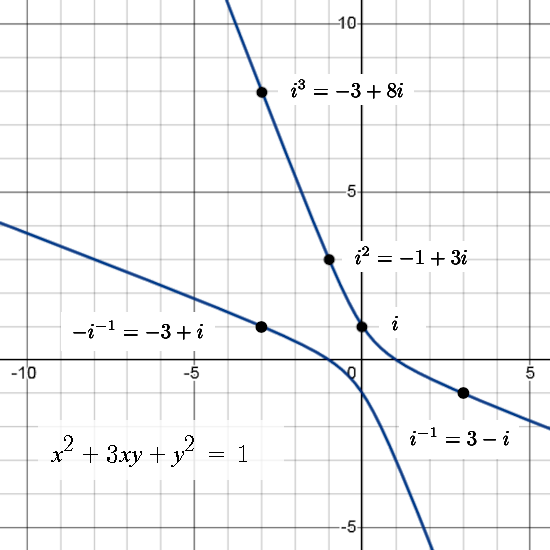
1) We looked at the matrix representations for 2D numbers ruled by i^2 = -1 + i. The determinant of such matrices was x^2 + xy + y^2. Therefore we wanted to know more about the ellipse that gives a determinant of 1.

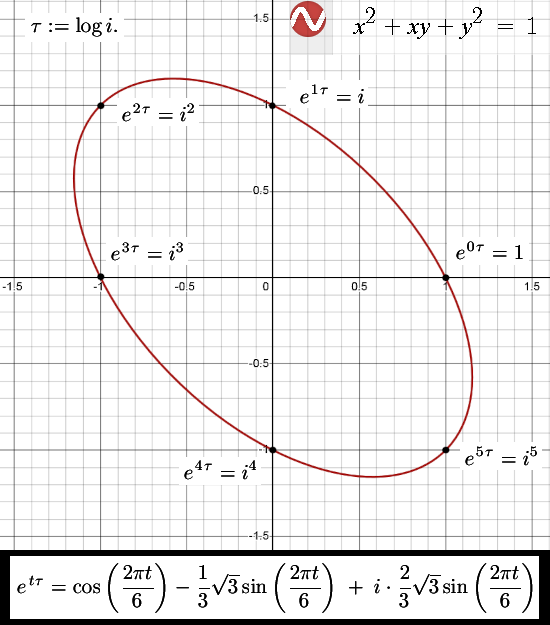
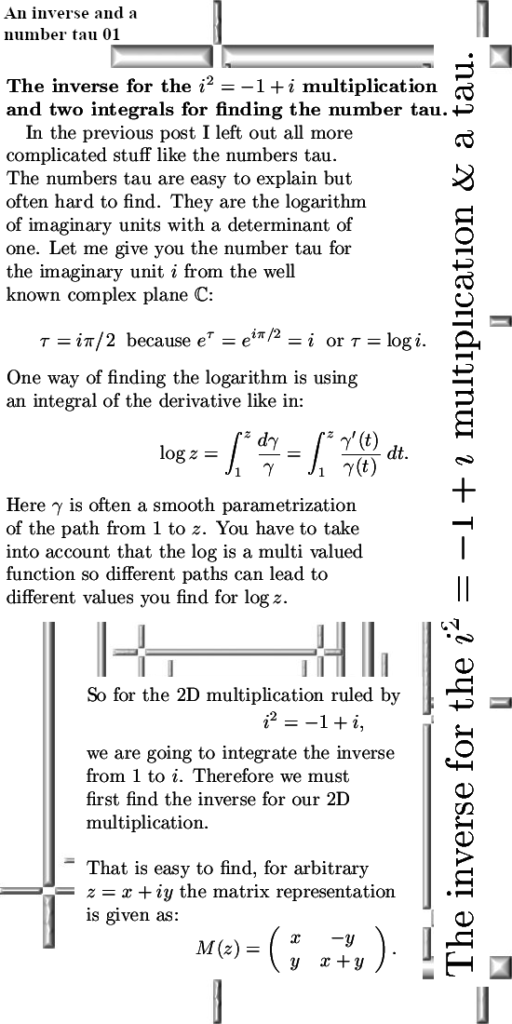
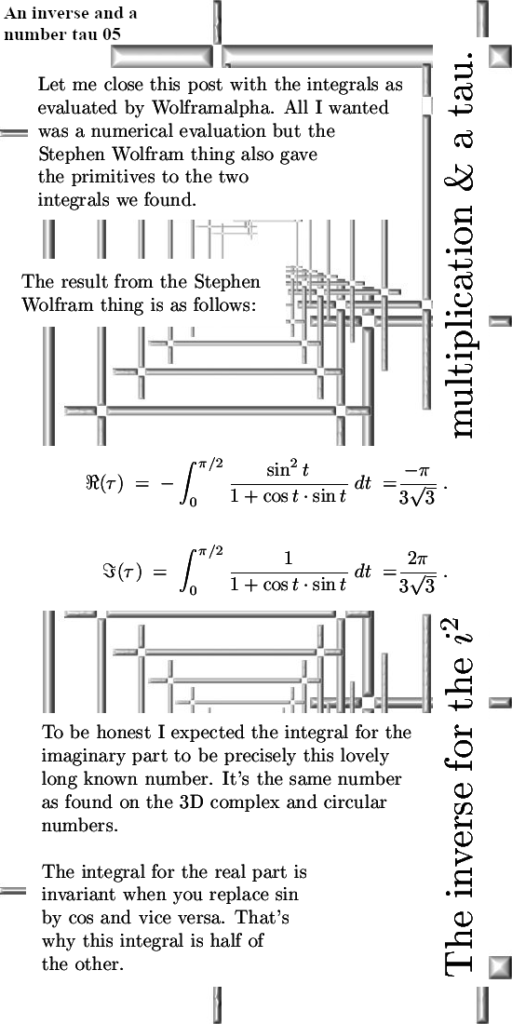
2) We found a way to take the logarithm of the imaginary unit i by taking the integral of the inverse from 1 to i. That is the number tau for this kind of multiplication. As such we had a complex exponential only now it covered that ellipse.

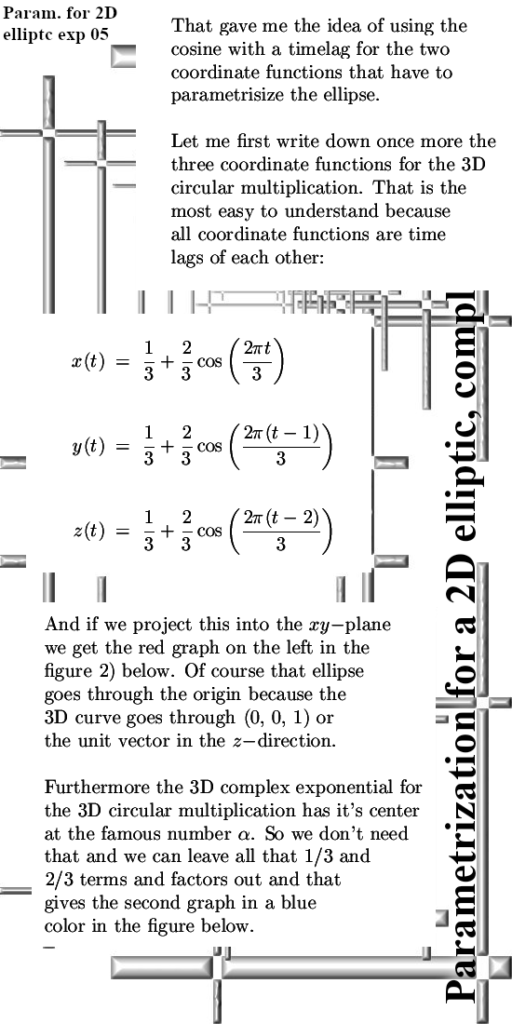
3) After that we had to find parametrizations of the complex exponential, actually we found two of them via very different idea’s. It was left totally unproven that the two were the same although in for example the Desmos graphing package they covered the same ellipse. (But that is not a real math proof of course).

4) That is this post: Penning down the de Moivre identity or formula for this particular kind of 2D multiplication. So we can end the recap here.

The post is seven pictures long and I made them a bit larger this time: 550×1200 pixels. There’s also two additional figures so all in all very much pictures for so little math. I like the end result a lot, ok ok it is not very deep math but it looks damn cute in my opinion.
So I hope you will have fun reading it and thinking about the math involved in this post on 2D multiplications.

Often when found for the first time, the math was formulated very differently.

Here is a link to a more general wiki upon Abraham de Moivre:
https://en.wikipedia.org/wiki/Abraham_de_Moivre.

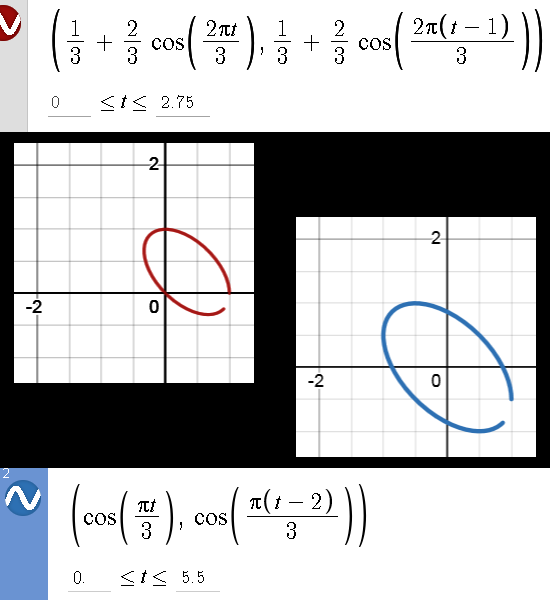
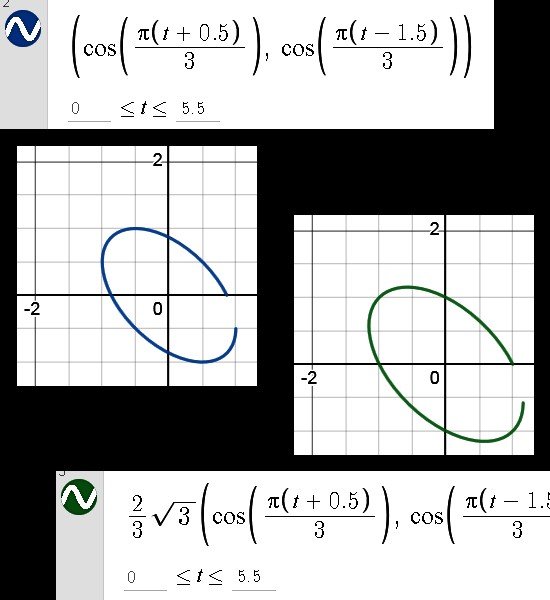
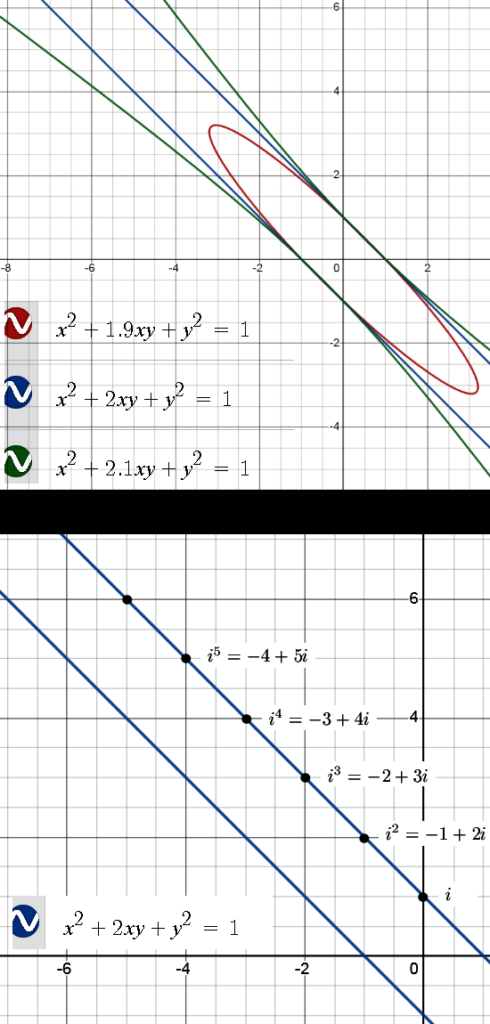
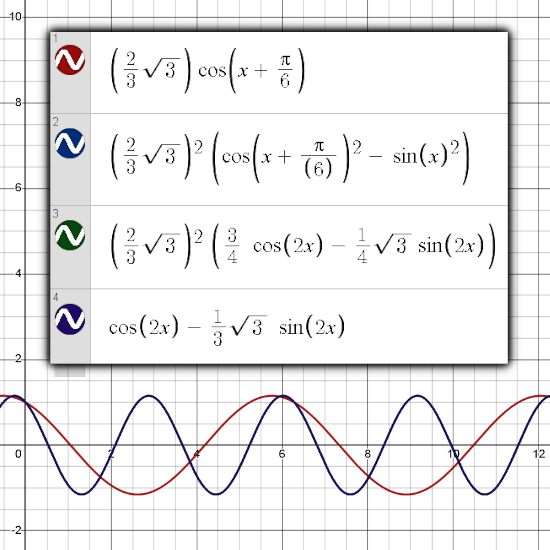
In the next figure you can see that three of the equations give rise to the same graph in the Desmos package while of course again remarking this is not what a math proof should be…
Please ignore the typo (6) in the equation for the blue graph while remarking that Desmos still spits out the correct answer.

Once more: This is not a proof but you can use it for a bit of relief that you’re on the right road.

That was it for this post. May be the next post is on the conjugate or may be a post on magnetic stuff. I don’t know yet but I do know I want to thank you for your attention.

Two parametrizations for the ‘unit’ ellipse in the i^2 = -1 + i kind of multiplication.

2D multiplications, 3D complex numbers, Exponential circle, Exponential curves

Basically this post is just two parametrizations of an ellipse, so all in all it should be a total cakewalk… So I don’t know why it took me so long to write it, ok ok there are more hobbies as math competing for my time. But all in all for the level of difficulty it took more time as estimated before.
In the last post we looked at the number tau that is the logarithm for the imaginary unit i and as such I felt obliged to at least base one of the parametrizations on that. So that will be the first parametrization shown in this post.
The second one is a projection of the 3D complex exponential on the xy-plane. So I just left the z-coordinate out and see what kind of ellipse you get when you project the 3D exponential circle on the 2D plane. Acually I did it with the 3D circular multiplication but that makes no difference only the cosines are now more easy to work with. Anyway the surprise was that I got the same ellipse back, so there is clearly a more deeper lying connection between these two spaces (the 3D circular numbers and these 2D complex multiplication defined by i^2 = -1 + i).
A part of the story as why there is a connection between these spaces is of course found into looking at their eigenvalues. And they are the same although 3D complex numbers have of course 3 eigenvalues while the 2D numbers have two eigen values. A lot of people have never done the calculation but the complex plane has all kinds of complex numbers z that each have eigenvalues too…
Anyway I felt that out of this post otherwise it would just become too long to read because all in all it’s now already 10 images. Seven images with math made with LaTex and three additional figures with sceenshots from the DESMOS graphical package.
By the way it has nothing to do with this post but lately I did see a video where a guy claimed he calculated a lot of the Riemann zeta function zero’s with DESMOS. I was like WTF but it is indeed possible, you can only make a finite approximation and the guy used the first 200 terms of the Riemann zeta thing.
At this point in time I have no idea what the next post will be about, may be it’s time for a new magnetism post or whatever what. We’ll wait and see, there will always pop something up because otherwise this would not be post number 254 or so.
Well here is the stuff, I hope you like it or enjoy it.

Figure 1: This parametrization is based on the number tau.
Figure 2: The projection in red, stuff without 1/3 and 2/3 in blue.
Figure 3: The end should read (t – 1.5) but I was to lazy to repair it.

That was it for this post, of course one of the reasons to write is that I could now file it under the two categories “3D complex numbers” and “2D multiplications” because we now have some connection going on here.
And I also need some more posts related to 3D complex numbers because some time ago I found out that the total number of posts on magnetism would exceed those of the 3D complex numbers.

And we can’t have that of course, the goal of starting this website was to promote 3D complex numbers via offering all kinds of insights of how to look at them. The math professors had a big failure on that because about 150 years since Hamilton they shout that they can’t find the 3D complex numbers. Ok ok, they also want it as a field where any non-zero number is invertible and that shows they just don’t know what they are talking about.
The 3D complex numbers are interesting simply because they have all those non-invertible numbers in them.

It is time to split my dear reader so we can both go our own way so I want to thank you for your attention.

An inverse and a number tau for the i^2 = -1 + i multiplication.

2D multiplications

This way of doing the complex multiplication keeps on drawing my attention because of the funny property that i^3 = -1. As such it has interesting parallels to the 3D complex number. For example the eigenvalues of this defining imaginary unit is the third root out of -1 (and it’s conjugate). That is in line with the results from the 3D numbers although over there 3D numbers have 3 eigenvalues and not 2.

In this post I want to show you a way to find the logarithm of this imaginary unit i via integrating the inverse from 1 to i. Just like on the real line if you integrate 1/x from 1 to say some positive a, you get log a. It is important to remark there are more methods to find such logarithms. For example you can diagonalize the multiplication and take the log of the eigenvalues and as such you can find the log of the imaginary unit.

Anyway back in the time I did craft my first complex exponential for the 3D complex numbers this way (using the integral of the inverse) so for me it is a bit of a walk down memory lane. You always get integrals that are hard to crack but if you use the WolframAlpha website it’s easy to find. Remarkably enough the two values for the integrals we will find below are also found in 3D and even the 6D complex numbers. So for me that was something new.

For myself speaking I loved the way the inverse of a complex number based on i^2 = -1 + i looks. You have to divide by the determinant once more proving that norms do not have very much to do with it. (In standard lessons on complex numbers it is always told that the norm of the product is the product of the norms, but that’s only so for the complex plane and the quaternions. So if you keep on trying such idea’s you won’t come very far…)

This post is five pictures long, lets go:

May be this parametrization is the next post.

Ok, that was it more or less for this post. Since we are now getting more and more posts on two dimensional complex (and split complex) numbers may be I will open a new category for those posts. On the other hand you must not open a new category every time you things that are a bit different from what you usually do…

2D elliptical and hyperbolic multiplications.

2D multiplications, Matrix representation

If you change the way the multiplication in the complex plane works, instead of a unit circle as the complex exponential you get ellipses and hyperbola. In this post I give a few examples, where usually the complex plane is ruled by i^2 = -1 we replace that by i^2 = -1 + i and i^2 = -1 + 3i.
In the complex plane the unit circle is often defined as the solution to the complex variable z multiplied against it’s conjugate and then solve where this product is one.
There is nothing wrong with that, only it leads to what is often told in class or college and that is: The norm of a product of two complex numbers is the product of the norms. And ok ok, on the complex plane this is true but in all other spaces the I equipped with a multiplication it was never true. It is the determinant that does all the work because after all on the complex plane the determinant of a matrix representation of the complex variable z is
x^2 + y^2. (Here as usual z = x + iy for real valued variables x and y.)

Therefore in this post we will solve for det(z) = 1 for the two modified multiplications we will look at. I did choose the two multiplications so that in both cases det(i) = 1. That has the property that if we multiply and z against i, the determinant stays the same; det(iz) = det(z).

I simply name complex z with integer x and y also integers, a more precise name would be Gaussian integers to distinguish them from the integers we use on the real line. Anyway I do not think it is confusing, it is rather logical to expect a point in the plane with integers coordinates to be an integer point or an integer 2D complex number z.

Beside the ellipses and hyperbola defined by det(z) = 1, or course there are many more as for example defined by det(z) = 3. Suppose we have some integer point or z on say det(z) = 3, if we multiply that z by i you stay on that curve. Furthermore such a point iz will always be an integer point to because after all the multiplication of integers is always an integer itself.
That is more or less the main result of this post; by multiplication with the modified imaginary unit i you hop through all other integer points of such an ellipse or hyperbole.
(By the way I use the word hyperbola to be the plural of hyperbole but I do not know if that is the ‘official’ plural for a hyperbole.)

What I found curious at first is the fact that expressions like z = -3 + 8i can have an integer inverse. But it has it’s own unavoidable logic: The 2×2 matrix representation contains only (real) integers and if the determinant is one, the inverse matrix will have no fractions whatsoever. The same goes for any square matrix with integer entries, if the determinant is one the inverse will also be a matrix with only integer entries.

This post is six pictures long, each size 550×1100 and three additional screen shots where I used the desmos graphics package for drawing ellipses and a hyperbole. At last I want to remark that I estimate these results as shown here are not new, the math community is investigating so called Diophantine equations (those are equations where you look for integer solutions) and as such a lot of people have likely found that there are simple linear relations between those integer solutions. Likely the only thing new here is that I modify the way the complex number i behaves as a square, as far as I know math folks never do that.
So let me try to upload the pictures and I hope you have fun reading it.

Funny detail: i^3 = -1.

Ok, that was it for this post. I hope you liked it and learned a bit of math from it. I do not have a good category for 2D numbers so I only file this under ‘matrix representations’ because those determinants do not fall from the sky. And file it under ‘uncategorized’.
Thanks for your attention and see you in a new post.

Addendum added 09 Dec 2023: I made a picture for the other website but since I made it already why not hang it in here too? See picture 05 above where we looked at when you get an elliptical multiplication and when the hyperbole version. In the picture below you see a rather weird complex exponential: a straight line. And the powers of i just hop over all those integer values on that line. The multiplication here is defined by i^2 = -1 + 2i. All positive powers hop to the left and upwards, the inverses go the other way. For example the inverse of i equals 2 – i.

Who would have thought that a complex exponential can be a line?

Ok, that was it for this post. Thanks for your attention.

Cauchy-Riemann equations for a ‘golden ratio’ 2D multiplication.

2D multiplications, CR equations

Even if you change the multiplication in the plane away from the complex or split complex multiplication it is always easy to find the famous CR-equations. And if you have those in the pocket you can differentiate functions defined on the space you made ‘just like’ on the real line.

After all the CR-equations only need that the numbers commute, you also need to make sure that all basis vectors have an inverse but that are the only restrictions. As far as I know in the math world of the universities the CR-equations are only used in the complex plane, may be some stuff with multiple complex variables and that’s all there is in that part of the math universe.

Originally I wrote the post in just one go and one day later when I read it I was rewarded with a lot of stupid typo’s. Stuff like mindlessly typing x and y where it should have been a and b, also I added the inverse of the imaginary unit because after all I said it was important in the previous post where we looked at CR-equations in the case of a more general n-dimensional space.

An interesting feature of the two dimensional plane is that the two basis vectors 1 and i always commute no matter what you come up with for i^2.
I hope the reader is familiar with the fact that on the complex numbers you have the square of i being minus one and plus one for the split complex numbers. In this post we will look at a 2D multiplication that is ruled by i^2 = 1 + i, so you can view this as a minor modification of the split complex numbers.

At first I named the multiplication a ‘strange multiplication’ but one day later I realized that the age old golden ratio has the same property as my imaginary unit i. If you square the golden ratio, that is also the same as the golden ratio plus one. So I renamed it to the golden ratio multiplication. I know it is a little click baity because the golden ratio itself is not used but only the polynomial equation you need to calculate the golden ratio. Universities have their multi-million marketing budgets, still can’t find 3D complex numbers by the way and I have my free tiny click baity golden ratio multiplication. I think it is an allowed sin.

Did you know that if there is something wrong with a product, it always needs massive marketing budgets. Just look at Coca Cola, without the advertisements the stuff should gradually sell less and less because it is not a healthy product. You can say it is an unhealthy product so there is something wrong with it and as such it needs all that marketing stuff in order to survive.

This post is only four pictures long, I hope it is a bit more easy to digest because it is only two dimensions. So lets go to the math in the four pictures:

Ok, that was it for this post. Thanks for your attention.