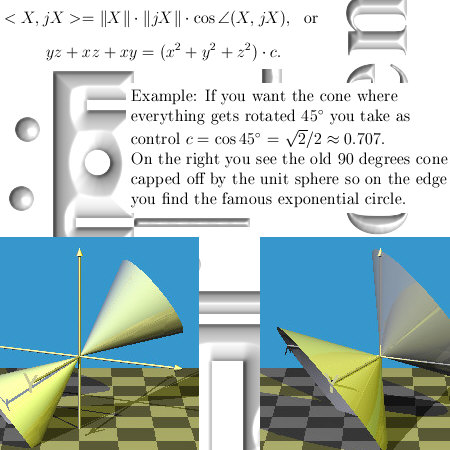
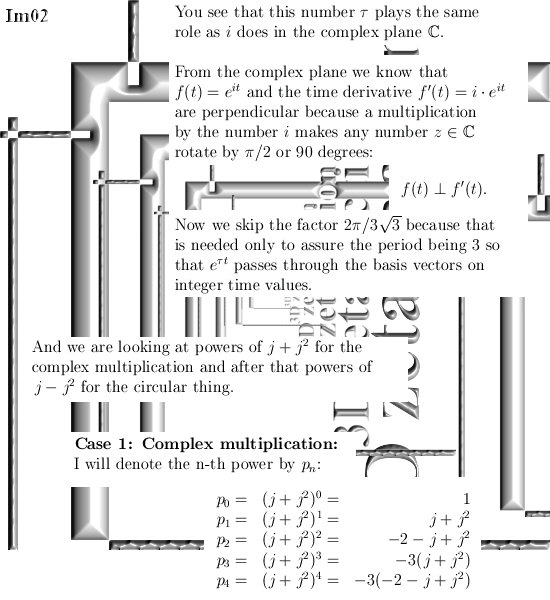
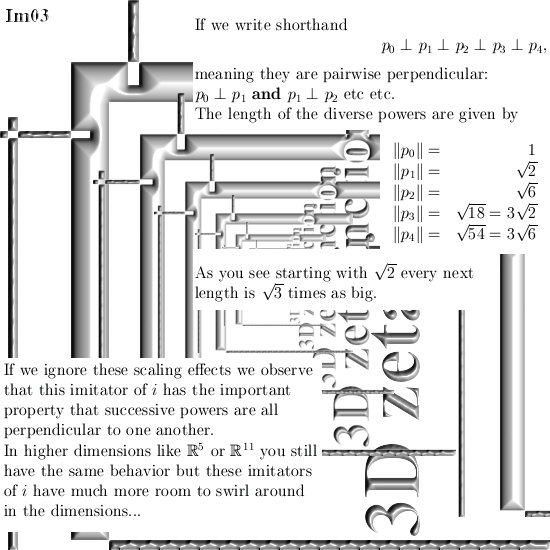
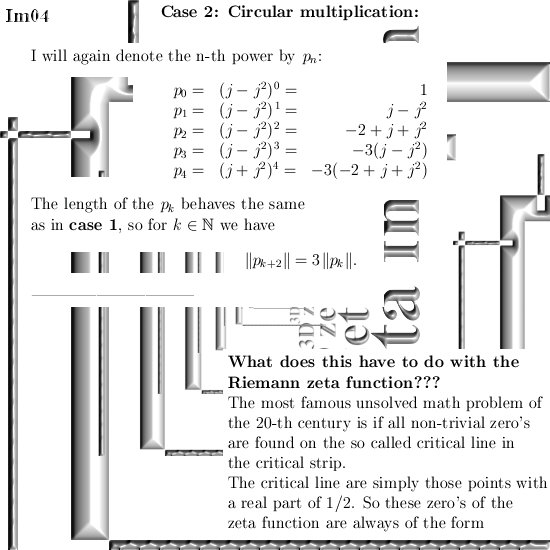
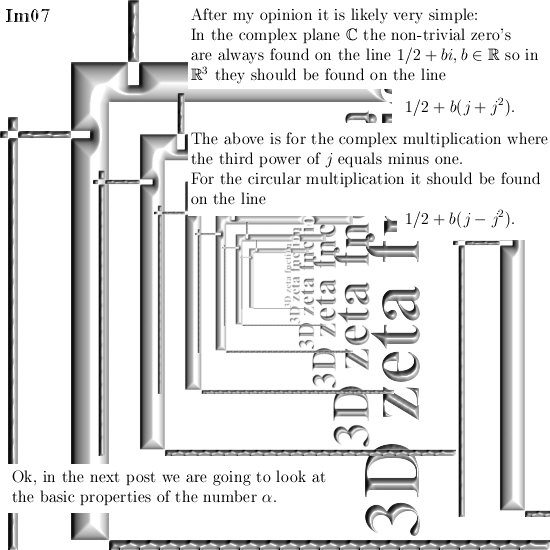
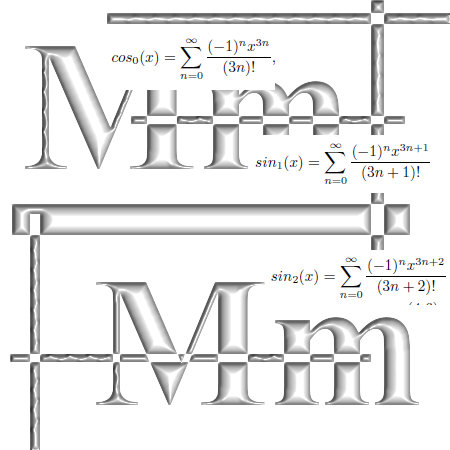
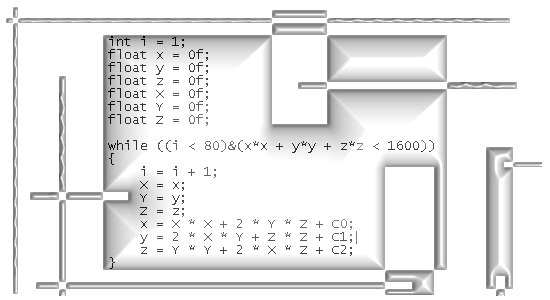
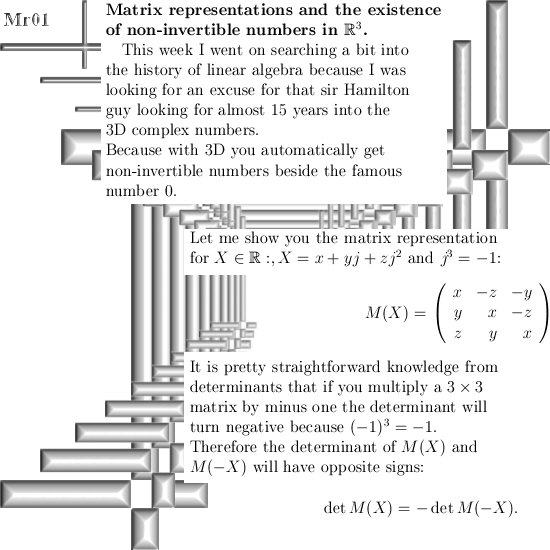
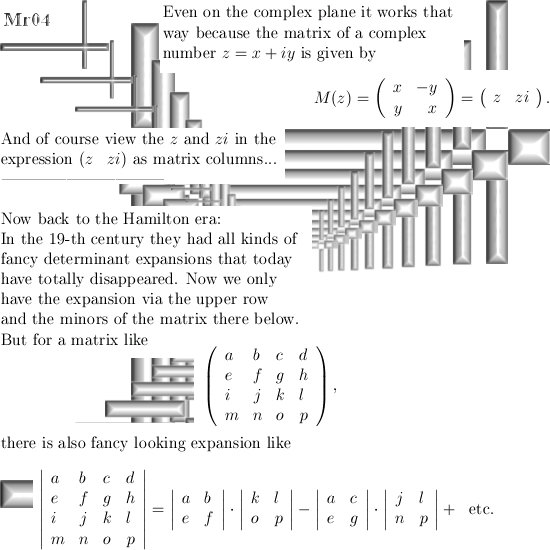
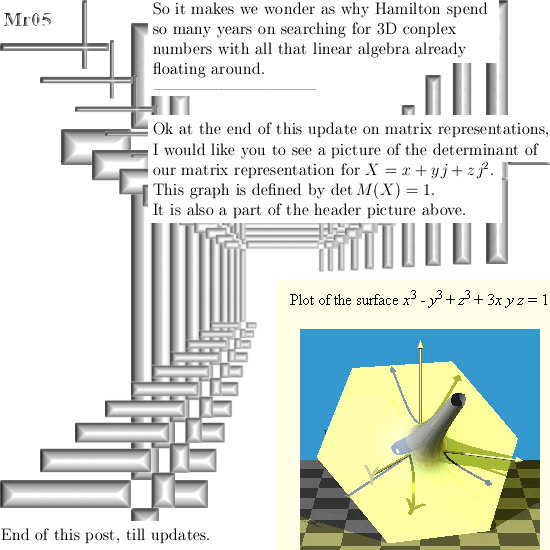
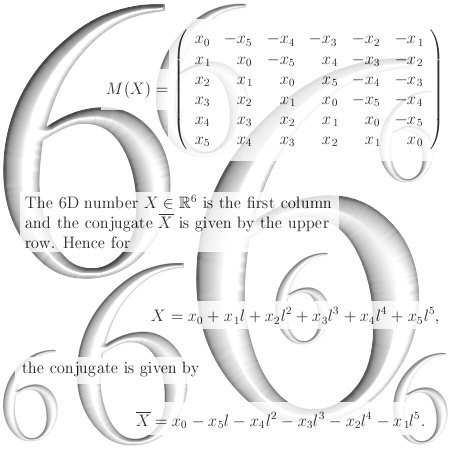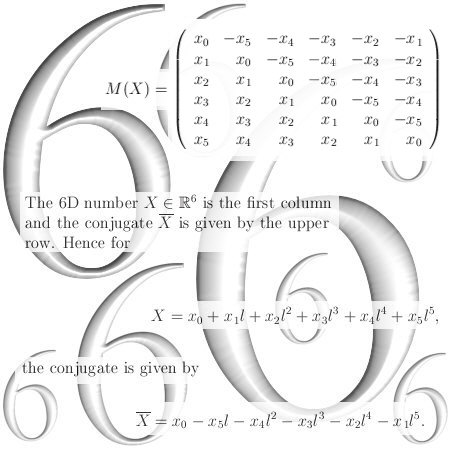On the other website I just posted 12 pages about the cone theorem. This theorem states that cones with a central axis the line through 0 and the number alpha and with their top in 0, undergo a fixed rotation when multiplied by one of the imaginary numbers like j or j^2.
You can find that on page four covering stuff posted this year.
It is important to remark I got the idea to study this particular detail because of the article in the preprint archive from Shlomo Jacobi. Now this Shlomo guy seems to be dead so I have to be a bit cautious. Let’s say these 12 pages are the way should study stuff like this & don’t forget I got the idea from this Jacobi guy while the professional math professors as usual contribute nothing.
In the next teaser picture you see how it works, while calculating some inner product you get this equation and if you fill in some allowed number for the control c you get the desired cone.
These cones are online easily made with an applet named Polyray. The great advantage of this applet is that you can fill in implicit equations so you are not bonded by some explicit stuff like
z = bla bla formulae in x and y.
You can click on the picture to land on the new update (open in a new window):
In another development I posted a few more reasons as why electrons are magnetic monopoles in the magnetic page on the other website. Now lately some folks from MIT have run six simulations of nuclear plasma and the results nicely confirm my insights in the behavior of nuclear plasma.
The MIT folks thought that in a nuclear fusion reactor you could simply neglect the contributions from the electrons because their mass is so small compared to the mass of protons and higher isotopes of atomic hydrogen. But ha ha ha, when electrons are magnetic monopoles such thinking is shallow & hollow. Anyway to make a long story short: the simulations point to a magnetic monopole electron.
Problem is I do not know how they model the plasma in detail, don’t forget the weirdo’s from the universities think electrons are magnetic dipoles and if you think that how can you make a reliable model of plasma anyway???
Here is the link around magnetic monopole stuff:
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm#17Feb2016
Enough of the bla bla bla, may be in the next post on this website I am going to dive into stuff related to the Schrödinger equation. Or something else like thousands and thousands of new and previously unknown trigoniometric identities…
We’ll see, till updates.